-
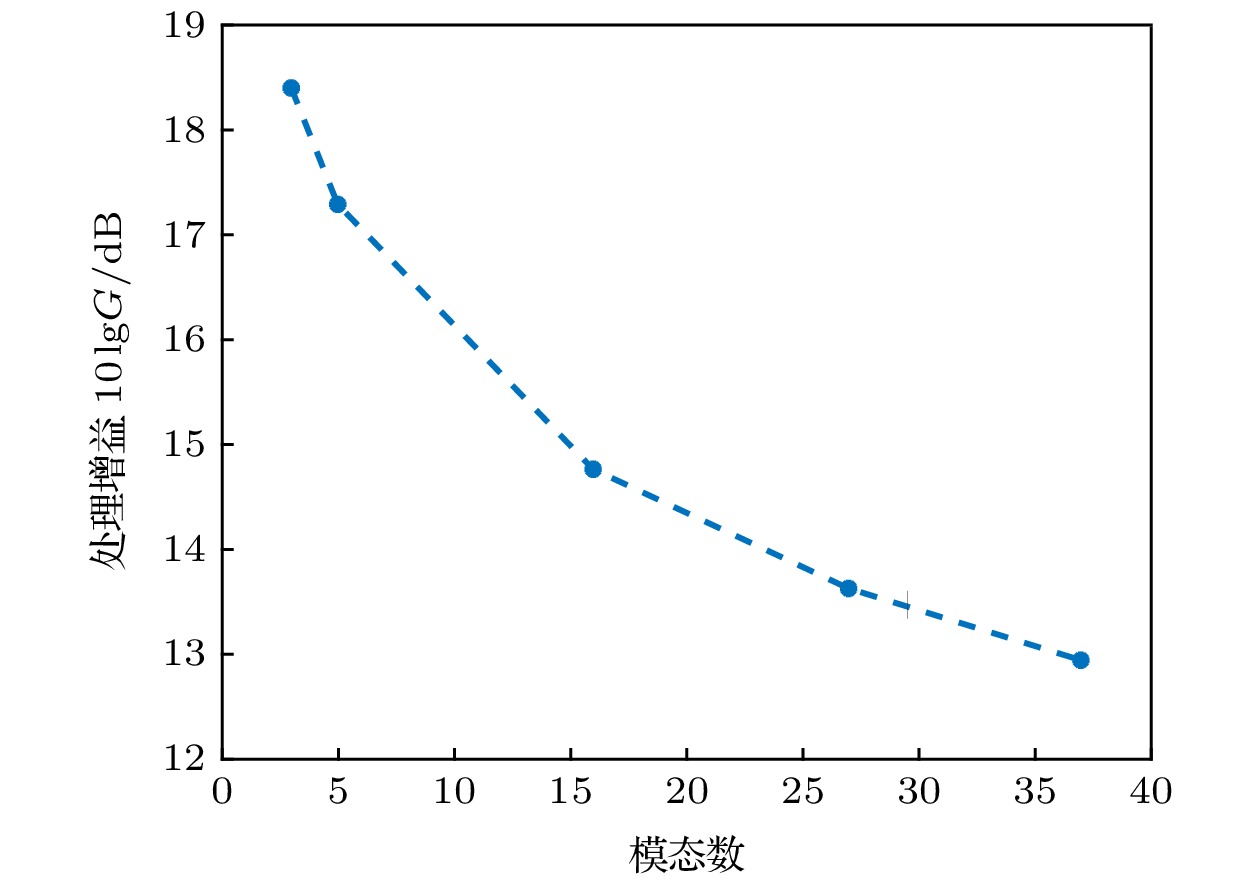
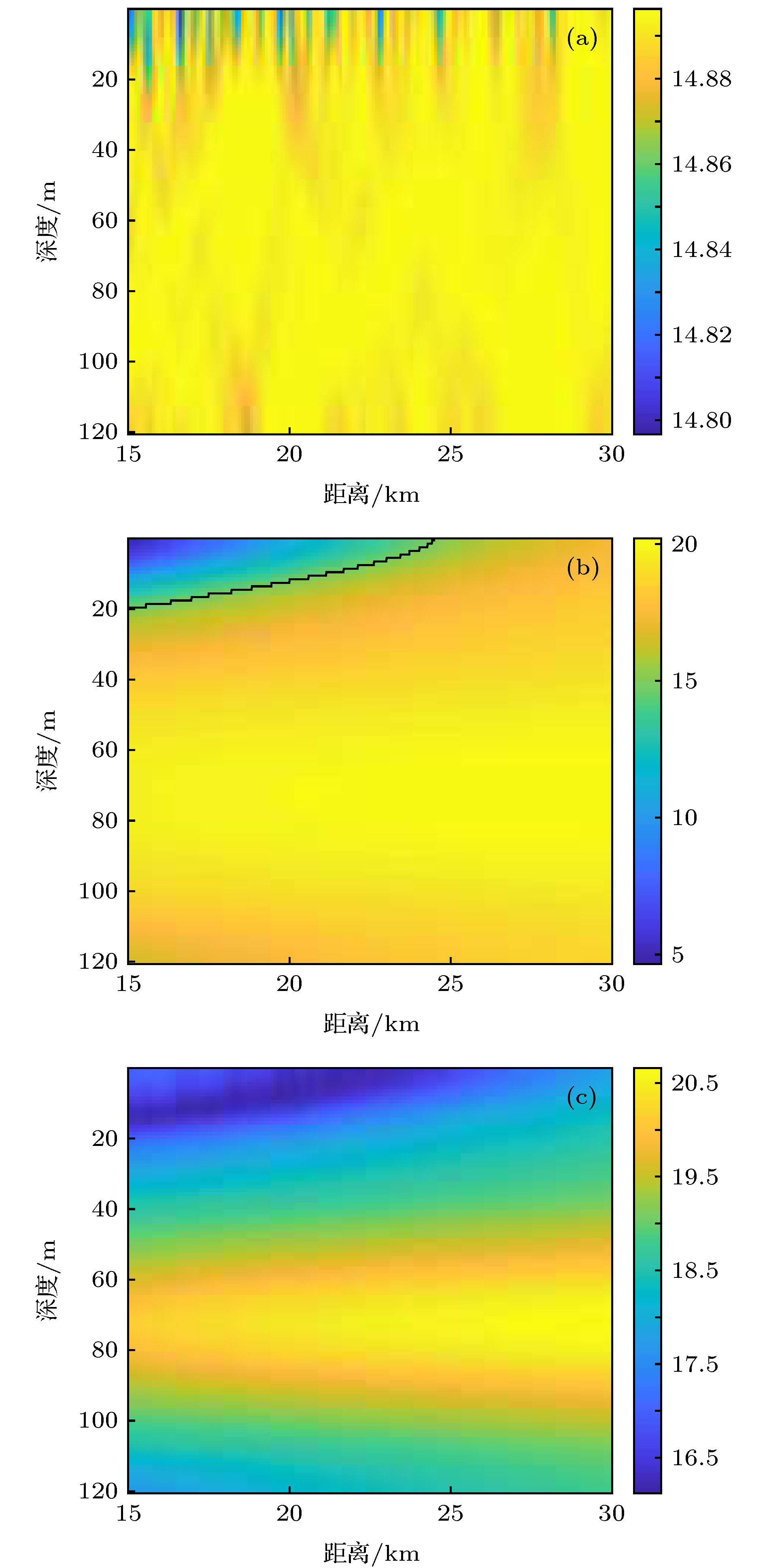
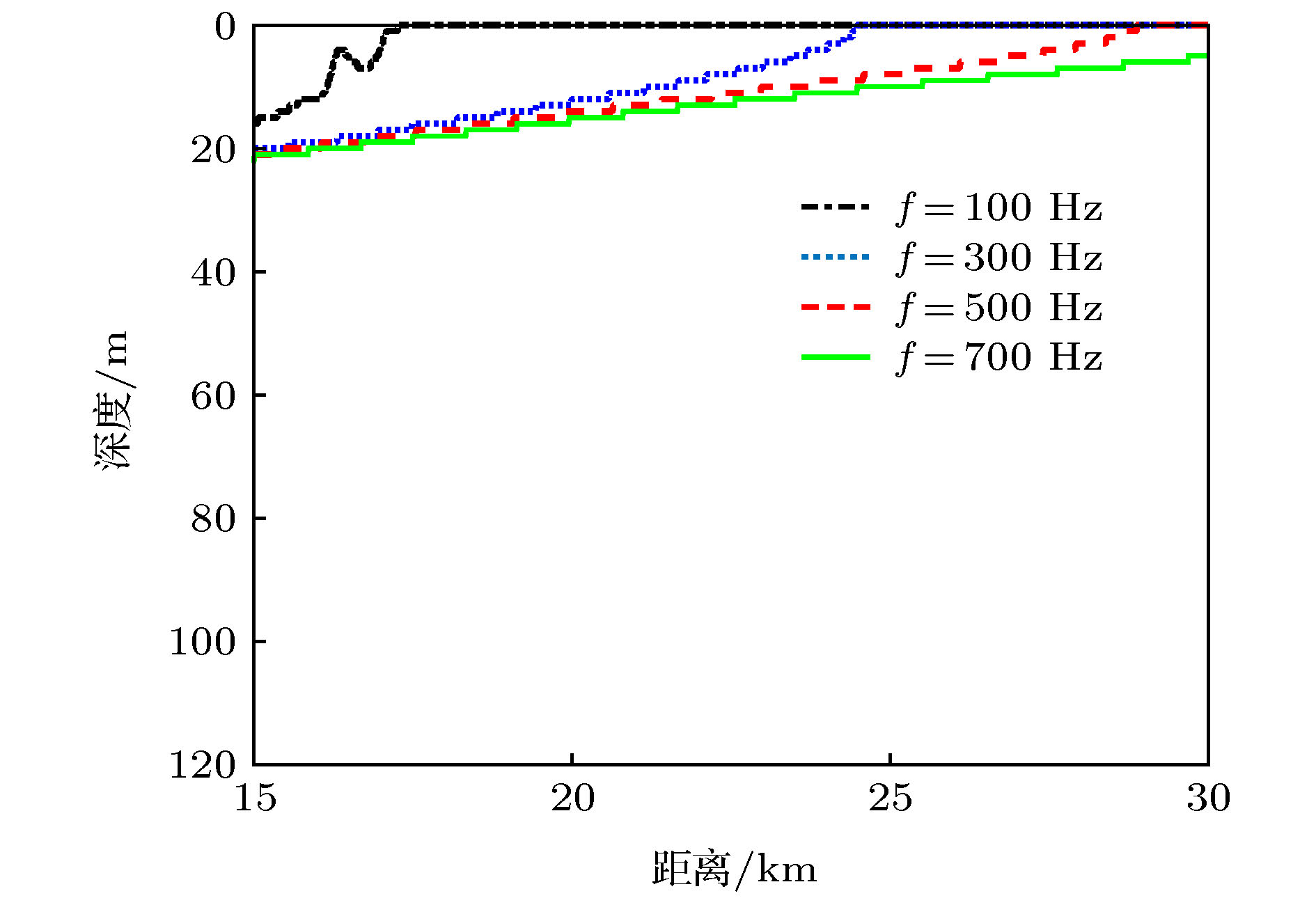
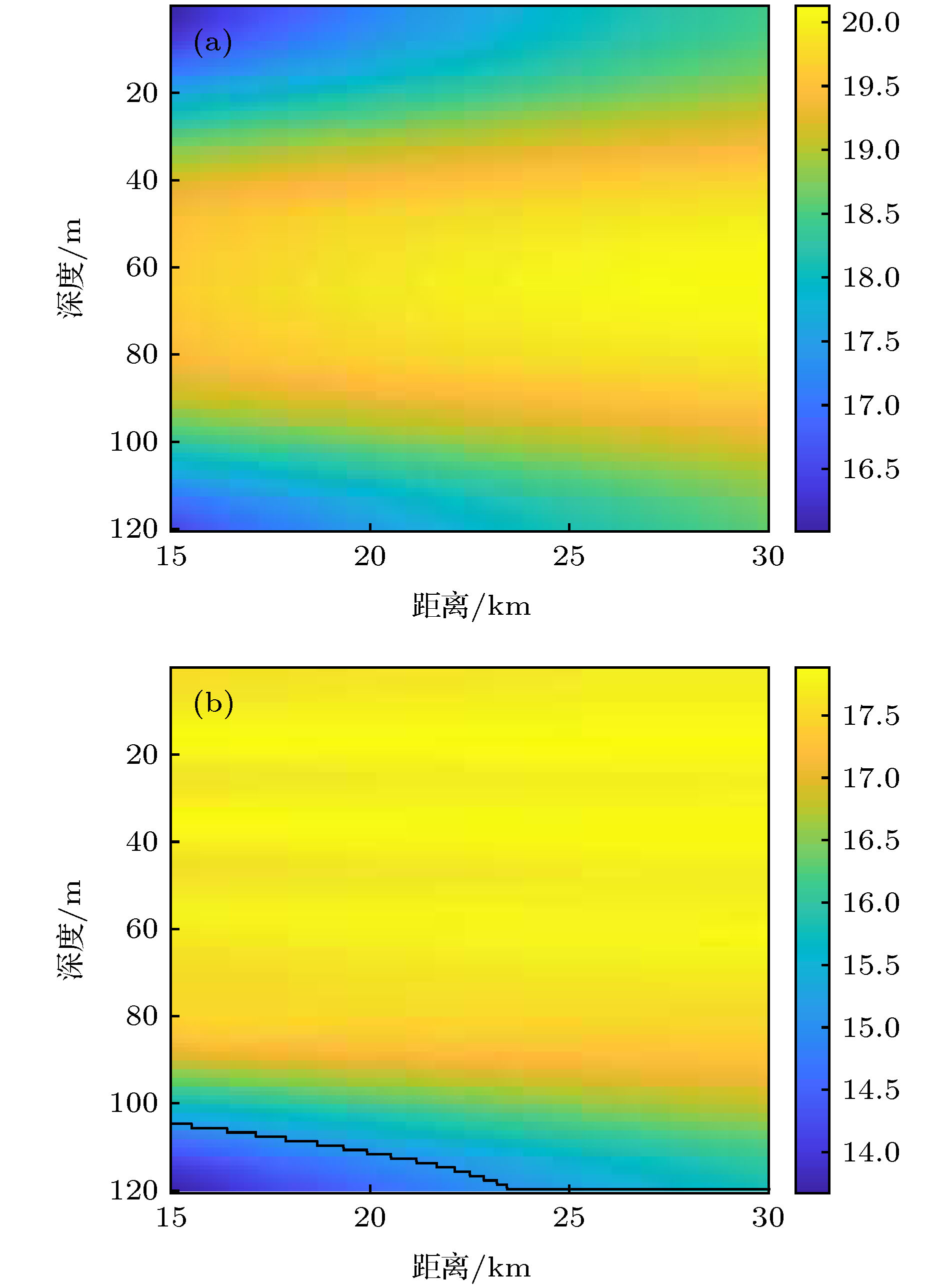
In this paper, the modal space detector (MSD) is investigated in shallow water environment when utilizing a vertical linear array. The processing gain of the MSD is derived, and the result demonstrates that the processing gain of the MSD degrades when the number of the propagated normal modes excited by the underwater acoustic source increases, and therefore the detection performance of the MSD decreases. By exploiting the orthogonality among the modal depth functions, the MSD can be decomposed into a group of modal subspace detectors (MSSDs). The processing gains of these MSSDs are derived as well and it is found out that the processing gain of a MSSD is in direct proportion to its corresponding modal attenuation coefficients. By designing a group of weighting coefficients based on the mode attenuation law, a weighted modal subspace detector (WMSSD) is proposed to alleviate the degradation of the processing gain processing of the MSD. We analyze the influences of acoustic source locations and sound velocity profiles (SVPs) on the detection performance of the WMSSD theoretically, and verify the theoretical analyses by comparing its processing gain with the MSD in simulation experiments. The results show that the WMSSD presents various processing gains versus different acoustic source locations. In the waveguide having a negatively-gradient SVP, there exists a ‘weak detection area’ for the WMSSD, that is, the processing gain of the WMSSD is smaller than that of the MSD when the acoustic source locations are close to sea surface. The reason is because there are inversion points on the lower-order modal depth functions and the depths of the inversion points are close to sea surface. In other most areas, the processing gain of the WMSSD is larger (even remarkably larger) than that of the MSD. In the waveguide having a positively-gradient SVP, due to the phenomenon that the modal inversion points of the lower-order modal depth functions are near sea floor, there is a contrary consequence, that is, the ‘weak detection area’ is close to sea floor. And meanwhile the WMSSD outperforms the MSD in other most areas as well. There are no modal inversion points in the waveguide having a constant SVP, and therefore the WMSSD always outperforms the MSD.
-
Keywords:
- modal space detection /
- modal attenuation coefficient /
- processing gain /
- modal inversion point
[1] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
 Google Scholar
Google Scholar
[2] Sha L, Nolte L W 2005 J. Acoust. Soc. Am. 117 1942
 Google Scholar
Google Scholar
[3] Sha L, Nolte L W 2006 IEEE J. Oceanic Eng. 31 345
 Google Scholar
Google Scholar
[4] 刘宗伟, 孙超, 易锋, 郭国强, 向龙凤 2014 声学学报 3 309
Liu Z W, Sun C, Yi F, Guo G Q, Xiang L F 2014 Acta Acust. 3 309
[5] 刘宗伟, 孙超, 吕连港 2015 声学学报 5 665
Liu Z W, Sun C, Lv L G 2015 Acta Acust. 5 665
[6] Scharf L L, Friedlander B 1993 IEEE Trans. Signal Process. 42 2146
[7] Krishna K M, Anand G V 2009 IEEE OCEANS Biloxi, USA, October 26−29, 2009 p1
[8] Hari V N, Anand G V, Premkumar A B, Madhukumar A S 2011 IEEE OCEANS Santander, Spain, June 6−9, 2011 p1
[9] Hari V N, Anand G V, Nagesha P V, Nagesha P V, Premkumar A B 2012 Proceedings of the 20th European Signal Processing Conference Bucharest, Romania, August 27−31, 2012 p1334
[10] Hari V N, Anand G V, Premkumar A B 2013 Digit. Signal Process. 23 1645
 Google Scholar
Google Scholar
[11] 李明杨, 孙超, 邵炫 2014 物理学报 20 204302
 Google Scholar
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 20 204302
 Google Scholar
Google Scholar
[12] Li M, Sun C, Willett P 2017 IEEE J. Oceanic Eng. 99 1
[13] Kong D Z, Sun C, Li M Y, Liu X H, Xie L 2019 IEEE Access 7 79644
 Google Scholar
Google Scholar
[14] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 物理学报 68 174301
 Google Scholar
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
 Google Scholar
Google Scholar
[15] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp258−263
[16] 张仁和 1979 声学学报 2 16
Zhang R H 1979 Acta Acust. 2 16
[17] Wang Q, Zhang RH 1990 J. Acoust. Soc. Am. 87 633
 Google Scholar
Google Scholar
[18] 汪德昭, 尚尔昌2013 水声学(第二版) (北京: 科学出版社) pp92−94
Wang D Z, Shang E C 2013 Underwater Acoustics (Vol. 2) (Beijing: Science Press) pp92−94 (in Chinese)
[19] 斯蒂芬Kay著 (罗鹏飞, 张文明译) 2011 统计信号处理基础 (北京: 电子工业出版社) 第573−574页
Kay S M (translated by Luo P F, Zhang W M) 2011 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp573−574 (in Chinese)
[20] Morgan D R, Smith T M 1990 J. Acoust. Soc. Am. 87 737
 Google Scholar
Google Scholar
-
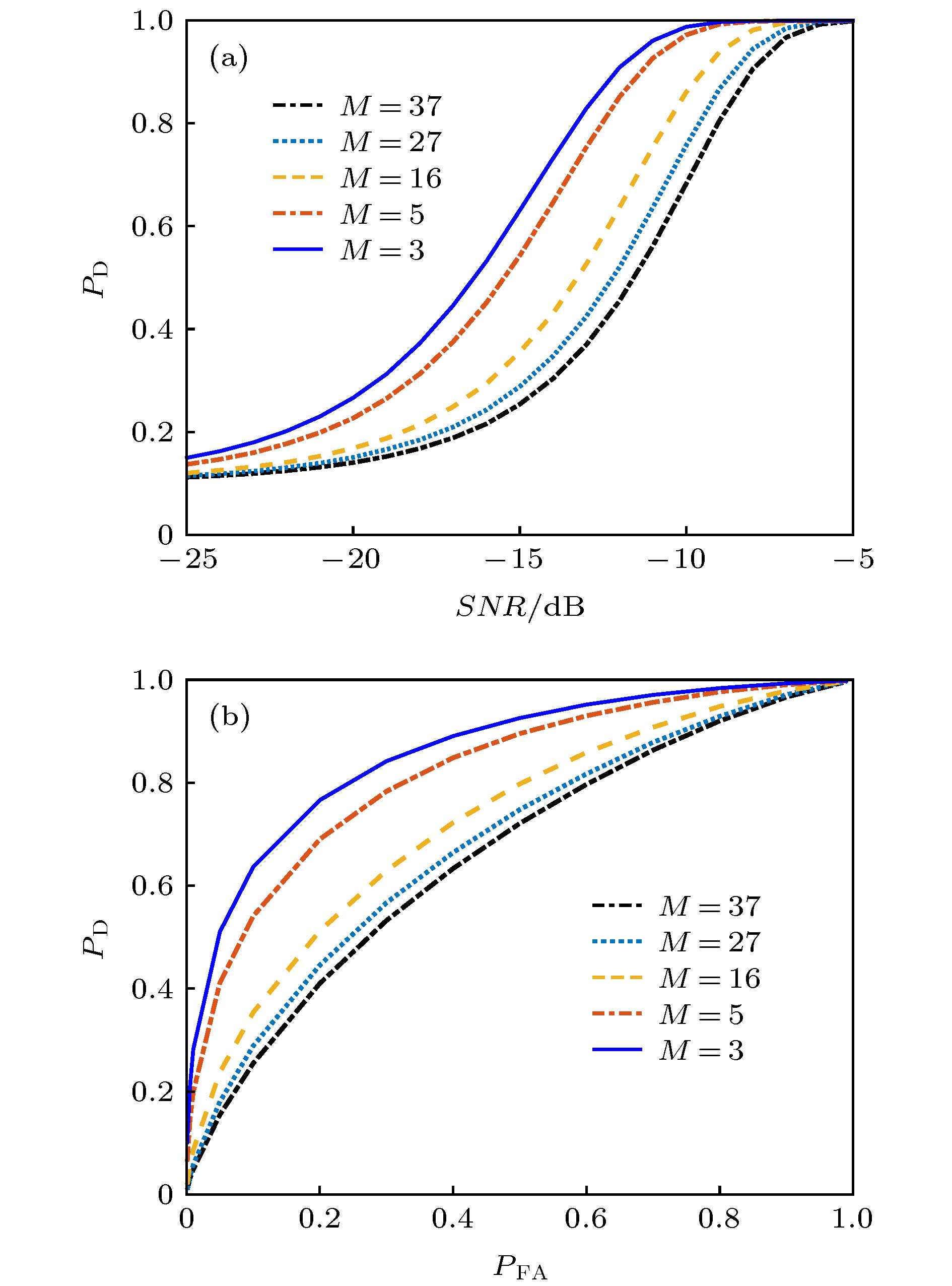
图 2 不同传播模态数下MSD的检测性能曲线 (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{ dB}}$ Figure 2. Detection performance curves of the MSD under various numbers of normal modes: (a) Probabilities of detection versus SNRs,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ .图 5 MSD, WMSSD, OWMSSD的检测性能曲线, f = 100 Hz (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{dB}}$ Figure 5. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 100 Hz: (a) Probabilities of detection versus SNR,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ .图 6 MSD, WMSSD, OWMSSD的检测性能曲线, f = 300 Hz (a) 检测概率随输入信噪比的变化,
${P_{{\rm{FA}}}} = 0.1$ ; (b) 检测概率随虚警概率的变化,$SNR = - 15\;{\rm{dB}}$ Figure 6. Detection performance curves of the MSD, WMSSD and OWMSSD with f = 300 Hz: (a) Probabilities of detection versus SNR,
${P_{{\rm{FA}}}} = 0.1$ ; (b) probabilities of detection versus probabilities of false alarm,$SNR = - 15\;{\rm{dB}}$ . -
[1] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401
 Google Scholar
Google Scholar
[2] Sha L, Nolte L W 2005 J. Acoust. Soc. Am. 117 1942
 Google Scholar
Google Scholar
[3] Sha L, Nolte L W 2006 IEEE J. Oceanic Eng. 31 345
 Google Scholar
Google Scholar
[4] 刘宗伟, 孙超, 易锋, 郭国强, 向龙凤 2014 声学学报 3 309
Liu Z W, Sun C, Yi F, Guo G Q, Xiang L F 2014 Acta Acust. 3 309
[5] 刘宗伟, 孙超, 吕连港 2015 声学学报 5 665
Liu Z W, Sun C, Lv L G 2015 Acta Acust. 5 665
[6] Scharf L L, Friedlander B 1993 IEEE Trans. Signal Process. 42 2146
[7] Krishna K M, Anand G V 2009 IEEE OCEANS Biloxi, USA, October 26−29, 2009 p1
[8] Hari V N, Anand G V, Premkumar A B, Madhukumar A S 2011 IEEE OCEANS Santander, Spain, June 6−9, 2011 p1
[9] Hari V N, Anand G V, Nagesha P V, Nagesha P V, Premkumar A B 2012 Proceedings of the 20th European Signal Processing Conference Bucharest, Romania, August 27−31, 2012 p1334
[10] Hari V N, Anand G V, Premkumar A B 2013 Digit. Signal Process. 23 1645
 Google Scholar
Google Scholar
[11] 李明杨, 孙超, 邵炫 2014 物理学报 20 204302
 Google Scholar
Google Scholar
Li M Y, Sun C, Shao X 2014 Acta Phys. Sin. 20 204302
 Google Scholar
Google Scholar
[12] Li M, Sun C, Willett P 2017 IEEE J. Oceanic Eng. 99 1
[13] Kong D Z, Sun C, Li M Y, Liu X H, Xie L 2019 IEEE Access 7 79644
 Google Scholar
Google Scholar
[14] 孔德智, 孙超, 李明杨, 卓颉, 刘雄厚 2019 物理学报 68 174301
 Google Scholar
Google Scholar
Kong D Z, Sun C, Li M Y, Zhuo J, Liu X H 2019 Acta Phys. Sin. 68 174301
 Google Scholar
Google Scholar
[15] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp258−263
[16] 张仁和 1979 声学学报 2 16
Zhang R H 1979 Acta Acust. 2 16
[17] Wang Q, Zhang RH 1990 J. Acoust. Soc. Am. 87 633
 Google Scholar
Google Scholar
[18] 汪德昭, 尚尔昌2013 水声学(第二版) (北京: 科学出版社) pp92−94
Wang D Z, Shang E C 2013 Underwater Acoustics (Vol. 2) (Beijing: Science Press) pp92−94 (in Chinese)
[19] 斯蒂芬Kay著 (罗鹏飞, 张文明译) 2011 统计信号处理基础 (北京: 电子工业出版社) 第573−574页
Kay S M (translated by Luo P F, Zhang W M) 2011 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp573−574 (in Chinese)
[20] Morgan D R, Smith T M 1990 J. Acoust. Soc. Am. 87 737
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 8679
- PDF Downloads: 61
- Cited By: 0















 DownLoad:
DownLoad: