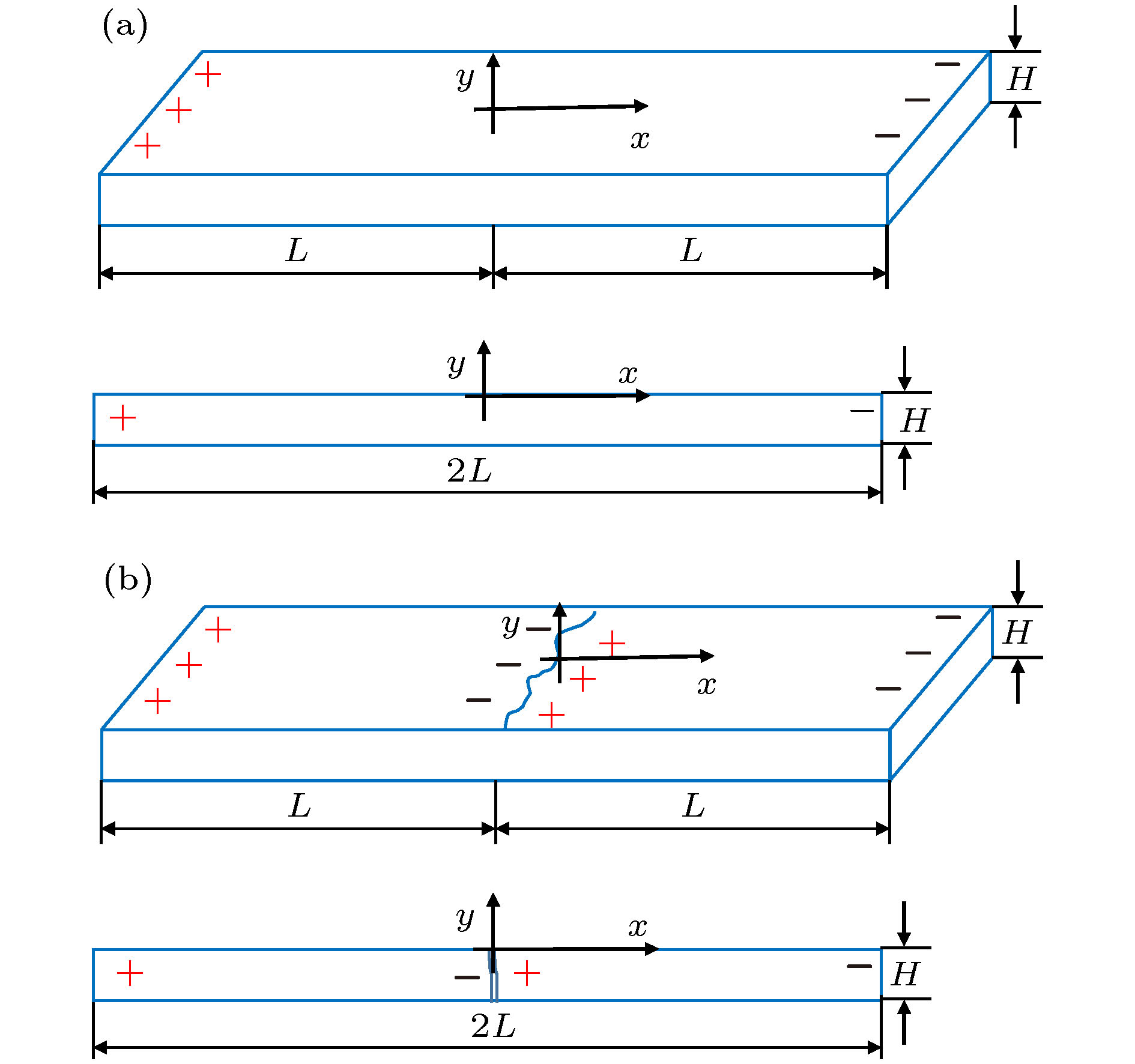
-
Magnetic dipole theory has been widely and successfully used to explain the leakage magnetic field signals. Because the model parameter such as magnetic dipole density is not easy to quantify, magnetic dipole theory often needs normalizing in application, which is considered to be unsuitable for quantitatively analyzing the magnetic memory signals with the stress effect. In this paper, the theoretical model of magneto-mechanical coupling magnetic dipole is established, which is suitable for analyzing the stress effect on magnetic signals in magnetic memory testing method. Based on the ferromagnetic theory, the equivalent field under the combined action of the applied load and the magnetic field is determined. And then, the magneto-mechanical analytical model is obtained for the isotropic ferromagnetic material under the weak magnetic field based on the first-order magnetization approximation in the weak magnetization state. Under the assumptions of rectangular and V-shaped magnetic charge distribution for the two-dimensional magnetic signal problem, the theoretical analytical models of the magnetic memory signals from the smooth and cracked specimens, and the analytical models of the magnetic memory signal induced by the rectangular and V-shaped surface defect are established. Based on the analytical solution of the proposed magneto-mechanical magnetic dipole theory, the difference in signal between before and after the failure of the specimen, the signal from the rectangular and V-shaped defect, and other influencing factors and laws of the magnetic signal are analyzed in detail. In particular, the influence of stress, environmental magnetic field, defect morphology and size, lift-off effect, specimen size and other factors on magnetic memory signals can be described based on the analytical solution of magneto-mechanical magnetic dipole models proposed in this paper. The proposed analytical model of magneto-mechanical magnetic dipole in this paper is simple and easy to use, and the present research shows that the proposed analytical solution in this paper can explain some basic experimental phenomena and laws in magnetic memory testing experiments. In addition, the precise magneto-mechanical coupling quantitative model combined with the finite element analysis method is still needed for accurately analyzing the magnetic memory signals in experiment.
-
Keywords:
- metal magnetic memory /
- magneto-mechanical coupling /
- magnetic dipole /
- analytical solution
[1] Dubov A A 1997 Met. Sci. Heat Treat. 39 401
Google Scholar
[2] Leng J C, Xu M Q, Li J W, et al. 2010 Chin. J. Mech. Eng. 23 532
Google Scholar
[3] Huang H H, Jiang S L, Yang C, et al. 2014 Nondestr. Test. Eval. 29 377
Google Scholar
[4] Minkov D, Lee J, Shoji T 2000 J. Magn. Magn. Mater. 217
Google Scholar
[5] 时朋朋 2015 无损检测 37 1
Shi P P 2015 Nondestr. Test. 37 1
[6] Wang Z D, Deng B, Yao K 2011 J. Appl. Phys. 109 083928
Google Scholar
[7] Li J W, Xu M Q 2011 J. Appl. Phys. 110 063918
Google Scholar
[8] Shi P P 2020 J. Magn. Magn. Mater. 512 166980
Google Scholar
[9] Avakian A, Ricoeur A 2017 J. Appl. Phys. 121 053901
Google Scholar
[10] Shi P P, Bai P G, Chen H E, et al. 2020 J. Magn. Magn. Mater. 504 166669
Google Scholar
[11] Zhong L Q, Li L M, Chen X 2013 IEEE Trans. Magn. 49 1128
Google Scholar
[12] Shi P P, Jin K, Zheng X J 2016 J. Appl. Phys. 119 145103
Google Scholar
[13] Shi P P, Jin K, Zhang P C, et al. 2018 IEEE Trans. Magn. 54 6202011
Google Scholar
[14] Zhang P C, Shi P P, Jin K, et al. 2019 J. Appl. Phys. 125 233901
Google Scholar
[15] Shi P P, Zhang P C, Jin K, et al. 2018 J. Appl. Phys. 123 145102
Google Scholar
[16] Shi P P, Zheng X J 2016 Nondestr. Test. Eval. 31 45
Google Scholar
[17] Shi P P, Su S Q, Chen Z M 2020 J. Nondestr. Eval. 39
Google Scholar
[18] Zhong L Q, Li L L, Chen X 2010 Nondestr. Test. Eval 25 161
Google Scholar
[19] Shi P P 2020 J. Appl. Phys. 128 115102
Google Scholar
[20] Shi P P, Jin K, Zheng X J 2017 Int. J. Mech. Sci. 124–125 229
Google Scholar
-
图 1 拉伸实验中的试件破坏前后的磁荷分布 (a)破坏前磁荷分布; (b)破坏后磁荷分布
Figure 1. Magnetic charge distribution before and after failure in tensile experiments: (a) Magnetic charge distribution before failure; (b) magnetic charge distribution after failure.
图 2 拉伸实验中试件破坏前和后的磁信号差异 (a) L = 100 mm; (b) L = 1000 mm
Figure 2. Difference of magnetic signals of the tensile specimen before and after failure: (a) L = 100 mm; (b) L = 1000 mm.
图 3 应力和外磁场对磁信号的影响 (a)应力影响; (b)外磁场影响
Figure 3. Effects of stress and external magnetic field on magnetic signals: (a) Stress effect; (b) effect of external magnetic field.
图 4 两种典型表面缺陷的磁荷分布示意图 (a)矩形凹槽试件; (b) V形凹槽试件
Figure 4. Schematic diagram of the magnetic charge distribution for two typical surface defects: (a) Rectangular groove defect specimen; (b) V-groove defect specimen.
图 5 缺陷深度对不同形貌缺陷诱导磁记忆信号的影响 (a)矩形凹槽; (b) V形凹槽
Figure 5. Effects of defect depth on magnetic signals induced by different shape defects: (a) Rectangular groove defect; (b) V-groove defect.
图 6 缺陷长度对不同形貌缺陷诱导磁信号的影响 (a)矩形凹槽; (b) V形凹槽
Figure 6. Effects of defect length on magnetic signals induced by different shape defects: (a) Rectangular groove defect; (b) V-groove defect.
图 7 应力和外磁场对矩形凹槽缺陷诱导磁信号的影响 (a)应力影响; (b)外磁场影响
Figure 7. Effects of stress and external magnetic field on magnetic signals induced by rectangular groove defects: (a) Stress effect; (b) effect of external magnetic field.
图 8 提离效应对试件磁信号的影响 (a)光滑试件; (b)具有矩形凹槽缺陷的试件
Figure 8. Effects of lift off on magnetic signals of specimen: (a) Smooth specimen; (b) specimen with rectangular groove defect.
图 9 试件尺寸对矩形凹槽缺陷试件磁信号的影响 (a)试件长度; (b)试件厚度
Figure 9. Effects of specimen size on magnetic signals with rectangular groove defect: (a) Effect of specimen length; (b) effect of specimen depth.
-
[1] Dubov A A 1997 Met. Sci. Heat Treat. 39 401
Google Scholar
[2] Leng J C, Xu M Q, Li J W, et al. 2010 Chin. J. Mech. Eng. 23 532
Google Scholar
[3] Huang H H, Jiang S L, Yang C, et al. 2014 Nondestr. Test. Eval. 29 377
Google Scholar
[4] Minkov D, Lee J, Shoji T 2000 J. Magn. Magn. Mater. 217
Google Scholar
[5] 时朋朋 2015 无损检测 37 1
Shi P P 2015 Nondestr. Test. 37 1
[6] Wang Z D, Deng B, Yao K 2011 J. Appl. Phys. 109 083928
Google Scholar
[7] Li J W, Xu M Q 2011 J. Appl. Phys. 110 063918
Google Scholar
[8] Shi P P 2020 J. Magn. Magn. Mater. 512 166980
Google Scholar
[9] Avakian A, Ricoeur A 2017 J. Appl. Phys. 121 053901
Google Scholar
[10] Shi P P, Bai P G, Chen H E, et al. 2020 J. Magn. Magn. Mater. 504 166669
Google Scholar
[11] Zhong L Q, Li L M, Chen X 2013 IEEE Trans. Magn. 49 1128
Google Scholar
[12] Shi P P, Jin K, Zheng X J 2016 J. Appl. Phys. 119 145103
Google Scholar
[13] Shi P P, Jin K, Zhang P C, et al. 2018 IEEE Trans. Magn. 54 6202011
Google Scholar
[14] Zhang P C, Shi P P, Jin K, et al. 2019 J. Appl. Phys. 125 233901
Google Scholar
[15] Shi P P, Zhang P C, Jin K, et al. 2018 J. Appl. Phys. 123 145102
Google Scholar
[16] Shi P P, Zheng X J 2016 Nondestr. Test. Eval. 31 45
Google Scholar
[17] Shi P P, Su S Q, Chen Z M 2020 J. Nondestr. Eval. 39
Google Scholar
[18] Zhong L Q, Li L L, Chen X 2010 Nondestr. Test. Eval 25 161
Google Scholar
[19] Shi P P 2020 J. Appl. Phys. 128 115102
Google Scholar
[20] Shi P P, Jin K, Zheng X J 2017 Int. J. Mech. Sci. 124–125 229
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8878
- PDF Downloads: 164
- Cited By: 0
