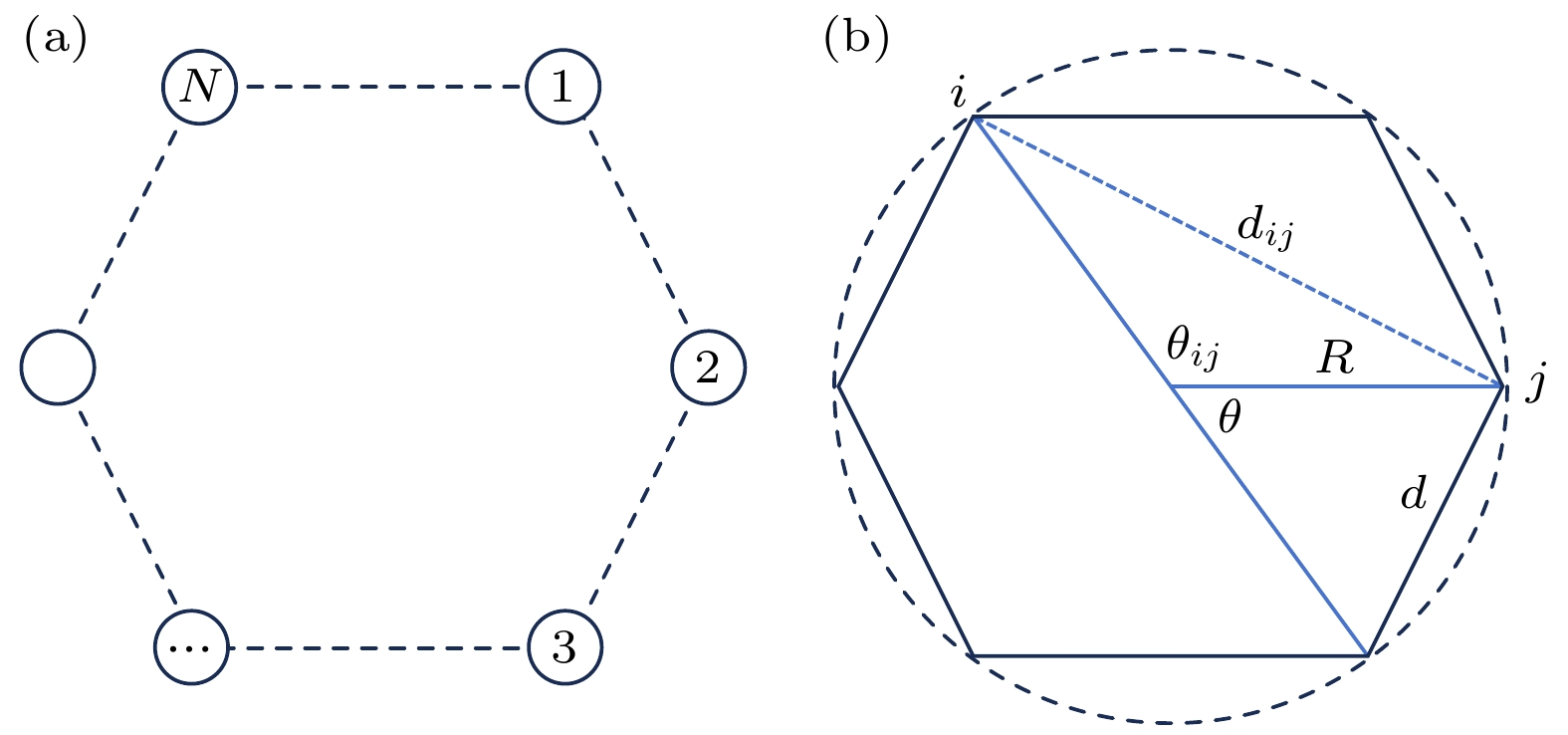
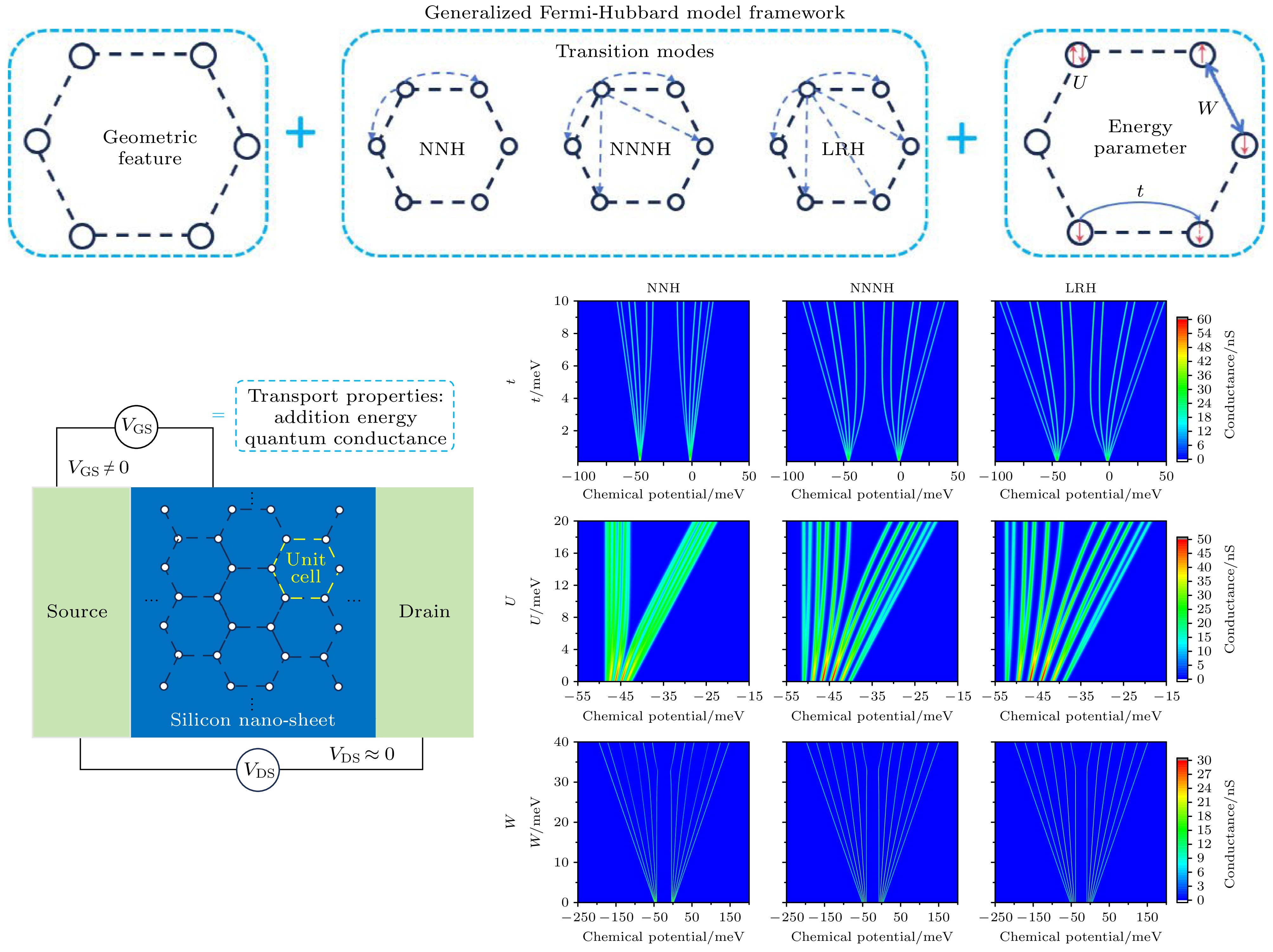
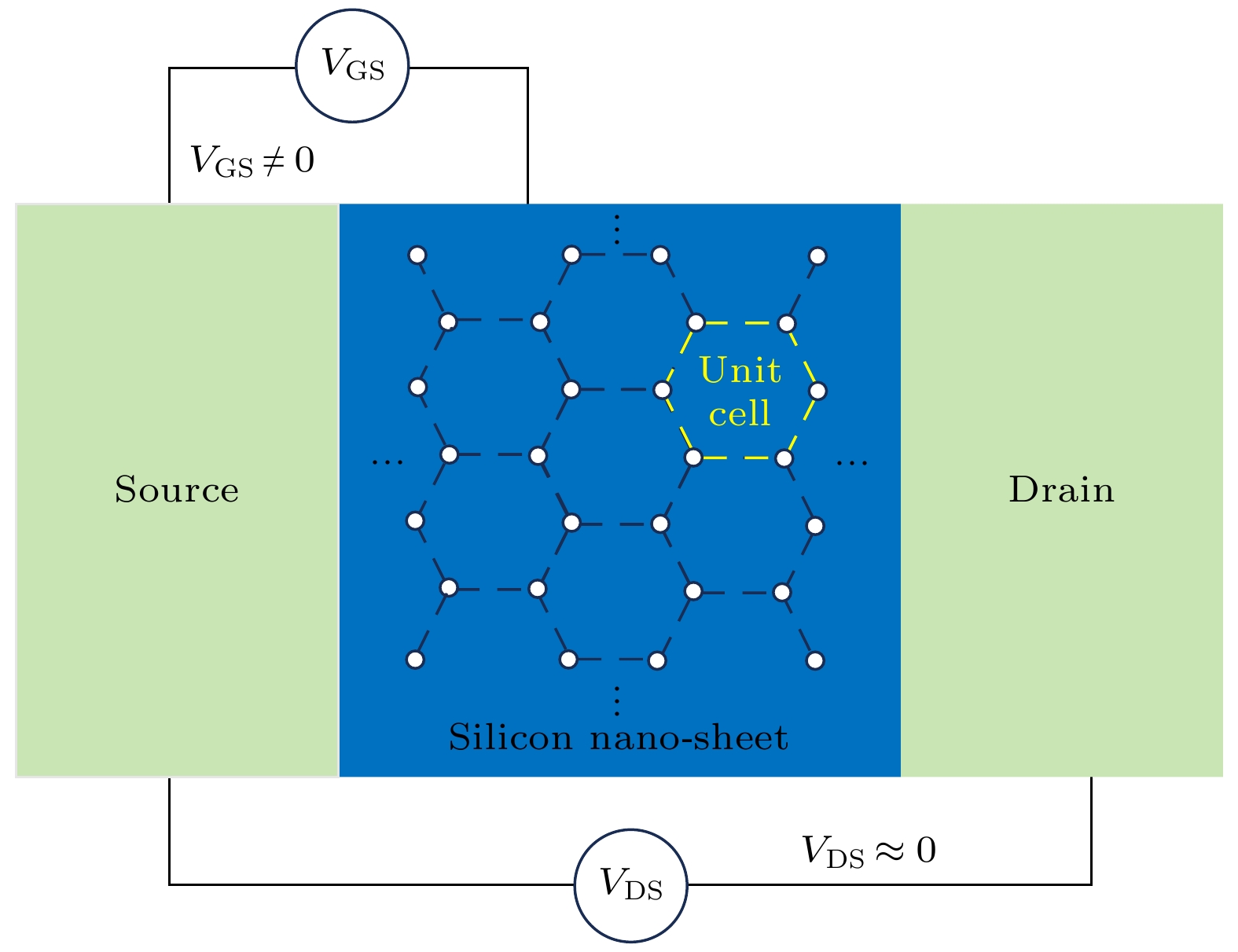
-
硅基纳米结构中杂质原子量子点阵列因其在量子计算、量子模拟等领域的巨大应用潜力而备受关注. 基于线形、环形和网状等不同几何结构排列的量子点阵列因拓扑特性的差异以及长程库仑相互作用的影响, 展现出各异的电子输运特性. 同时, 通过调控电子隧穿和波函数相位相干性, 可以深刻影响电子的跃迁输运行为. 本文致力于构建硅基纳米结构中杂质原子量子点阵列的通用Fermi-Hubbard模型, 探讨量子点分布的几何构型对电子的跃迁输运行为的调控机制. 特别以环形量子点阵列为例, 深入分析了不同几何结构和电子跃迁模式下的电子添加能谱与电导特性, 揭示了位间电子库仑排斥能、电子-离子实长程库仑吸引能与量子点耦合对电子跃迁行为的影响, 为理解量子点阵列几何分布对跳跃电子输运特性的调控机制提供了基本理论框架.
-
关键词:
- 量子点阵列 /
- 电子跃迁 /
- 几何构型 /
- 通用Hubbard模型
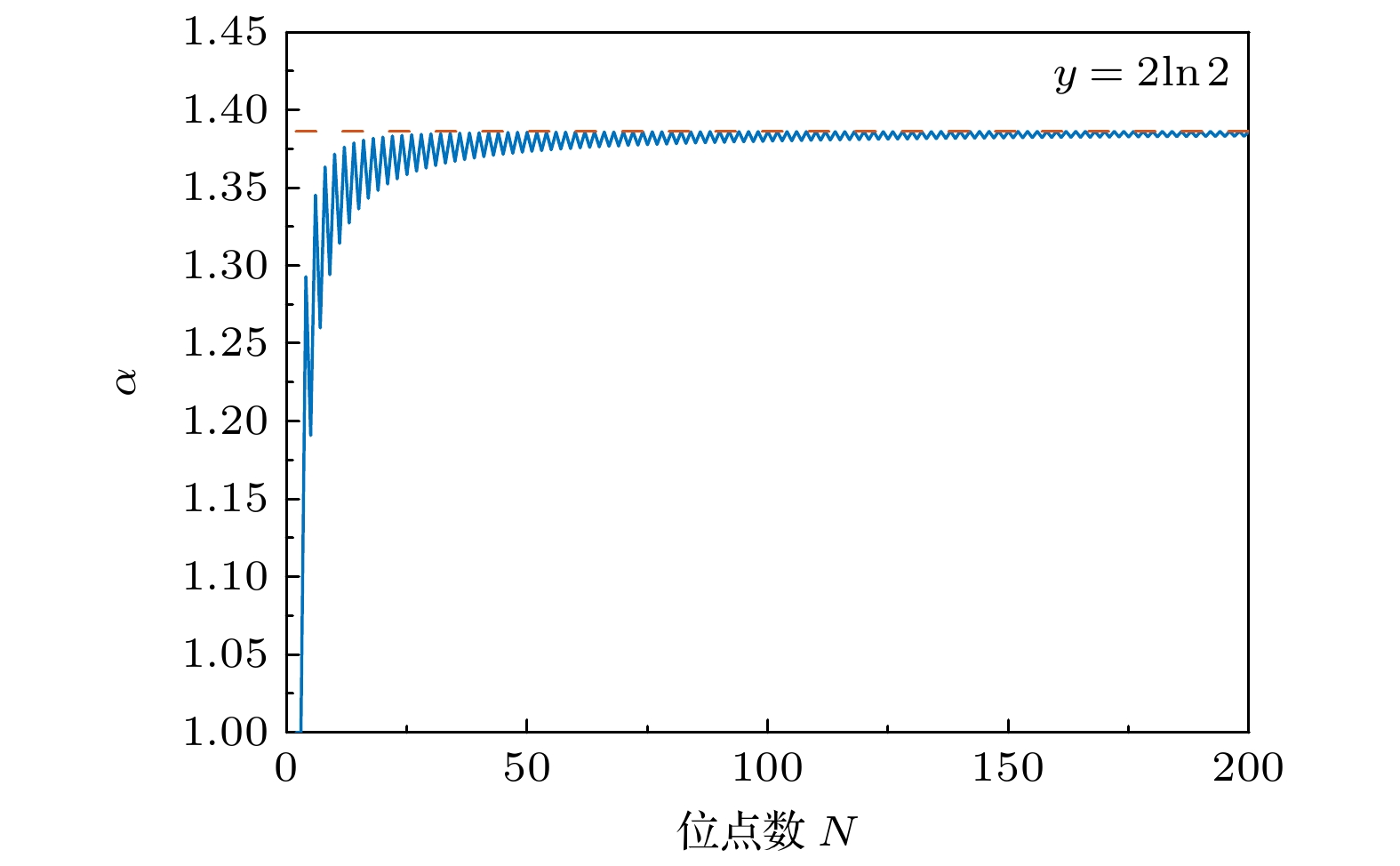
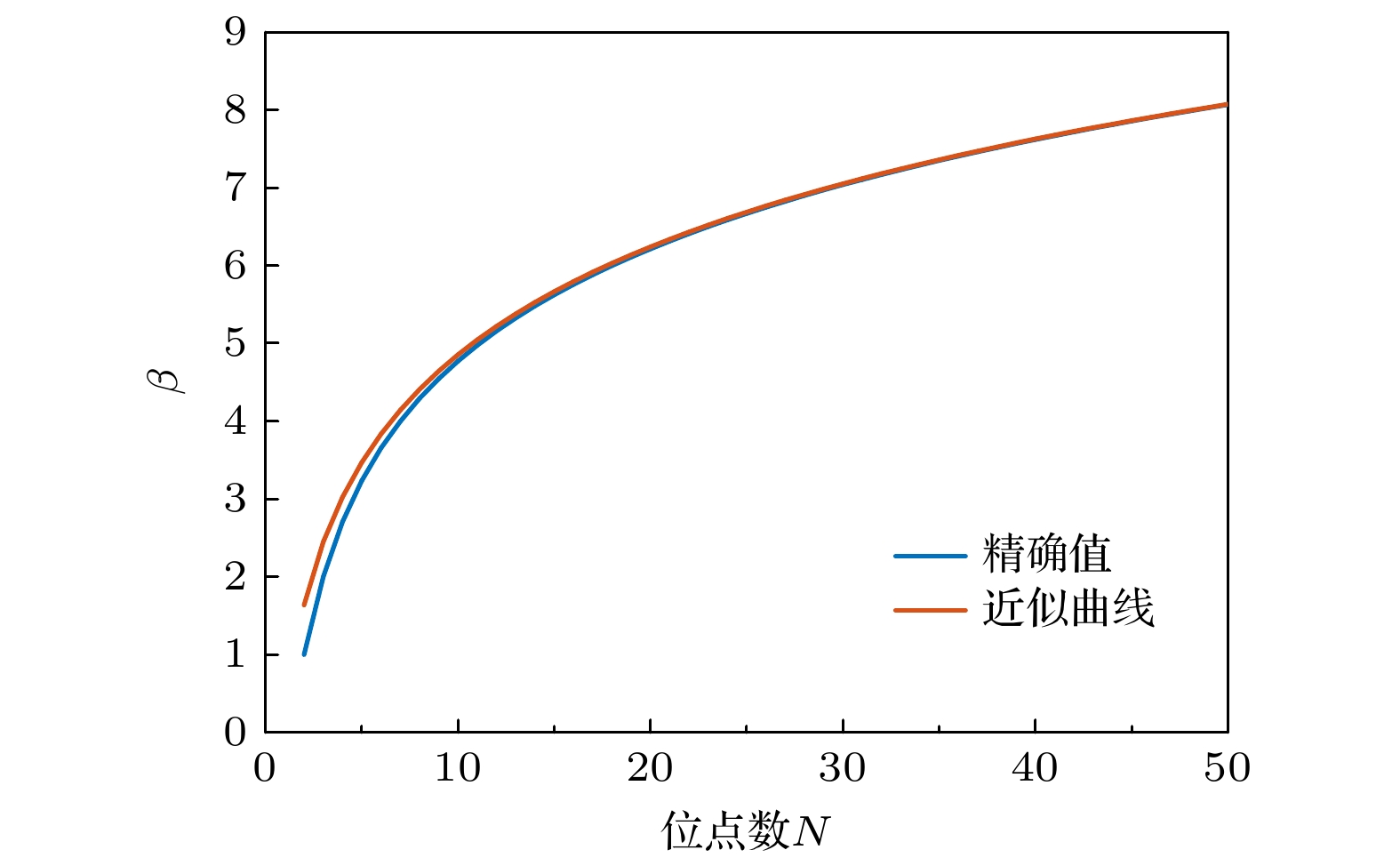
Dopant-induced quantum dot arrays in silicon-based nanostructures have received much attention due to their great potential applications in fields such as quantum computing and quantum simulation. When quantum dots are arranged in different geometric configurations such as linear, annular, or grid shapes, the differences in their inherent topological properties will lead to significantly different spatial distributions of the Coulomb interaction potential. The potential field distribution directly affects the phase coherence of electron wavefunctions, thereby regulating the dynamic behaviors of electrons such as electron tunneling and hopping between quantum dots, and greatly influencing the electron transport properties in the system. Our study aims to establish a basic theoretical framework to clarify the regulation mechanism of quantum dot geometric configurations on electron hopping transport. Therefore, we construct a universal Fermi-Hubbard model for silicon-based dopant-induced quantum dot arrays. The model defines the distance between quantum dots through an effective Euclidean distance matrix ( D ), which uniquely determines the geometric shape of the array, and defines the allowed electron hopping modes through an adjacency matrix ( A ). Using the framework and exact diagonalization method, we perform detailed numerical simulations on the electron transport properties in the traditional unit cell of two-dimensional ordered distribution dopant-induced quantum dot arrays. Generally, the primitive unit of a two-dimensional orderly distributed dopant-induced quantum dot array is a regular polygon that satisfies specific translational and rotational symmetries. We thereby refer to the quantum dot arrays distributed according to regular polygons as annular arrays. The geometric features of annular quantum dot arrays and the electron hopping modes including nearest-neighbor hopping (NNH), next-nearest-neighbor hopping (NNNH) and long-range hopping (LRH), exhibit significant regulation of the electron addition energy and quantum conductance. The regulation arises from interactions of key energy parameters, including coupling strength (t), on-site Coulomb repulsion (U) and inter-site Coulomb repulsion (W). In the electron addition energy spectrum, such a regulation is manifested in two aspects: energy band broadening and Coulomb gap size. Band broadening is co-regulated by t and W. Under weak coupling conditions, the broadening Δt induced by coupling strength is proportional to t, with its proportional coefficient increasing with the number of hopping paths (LRH > NNNH > NNH). The broadening ΔW caused by inter-site Coulomb repulsion is proportional to W, with the proportional coefficient being β, which is a geometry-dependent correlation broadening coefficient. In multi-site annular arrays, β exhibits a logarithmic relationship with the site number N. The size of Coulomb gap is co-influenced by U, t and W. The competition between U and W determines the electron configuration mode (dominated by single-electron occupation of sites or double-electrons occupation of spaced sites), with a critical value α for electron configuration reconstruction that causes a change in electron configuration across the threshold. When U/W > α, single-electron occupation dominates, and the gap is determined by the competition between U and t; when U/W < α, double-electrons occupation dominates, the gap expands under the influence of W, accompanied by the formation of sub-bands. In the quantum conductance spectrum, regulation is reflected in the distribution of conductance peak intensity. Geometric characteristics significantly affect peak intensity distribution. Linear arrays exhibit concentrated peak intensities due to edge states formed by open boundaries. While annular arrays with periodic boundaries and no edge states show more uniform peak distributions. Additionally, in annular arrays, the electron transport direction is non-collinear with the inter-site repulsion direction, endowing them with stronger robustness against transport inhibition induced by W. The influence of hopping modes is twofold. More hopping paths (LRH > NNNH > NNH) result in more non-zero hopping matrix elements, which causes higher average conductance. Meanwhile, hopping paths affect the phase coherence of wavefunctions, modulating the intensity of individual conductance peaks and forming distinct distribution. In conclusion, we establish a theoretical framework to clarify the physical mechanism, in which the geometric configurations and electron hopping modes of silicon-based dopant-induced quantum dot arrays regulate electron transport properties through synergistic interactions with key energy parameters (t, U, W). Electron addition energy spectra and quantum conductance spectra reveal the regulatory rules of these factors on electron transport behaviors, providing a theoretical guidance for optimally designing silicon-based quantum devices. 
-
Keywords:
- quantum dot arrays /
- electron hopping /
- geometric configuration /
- generalized extended Fermi-Hubbard model
-
图 1 硅基杂质原子晶体管结构示意
Fig. 1. Schematic of silicon-based dopant atom transistor structure.
图 2 (a) 环形阵列杂质原子分布; (b) 正多边形的几何关系
Fig. 2. (a) Annular array dopant atoms distribution; (b) geometric relationships of regular polygons.
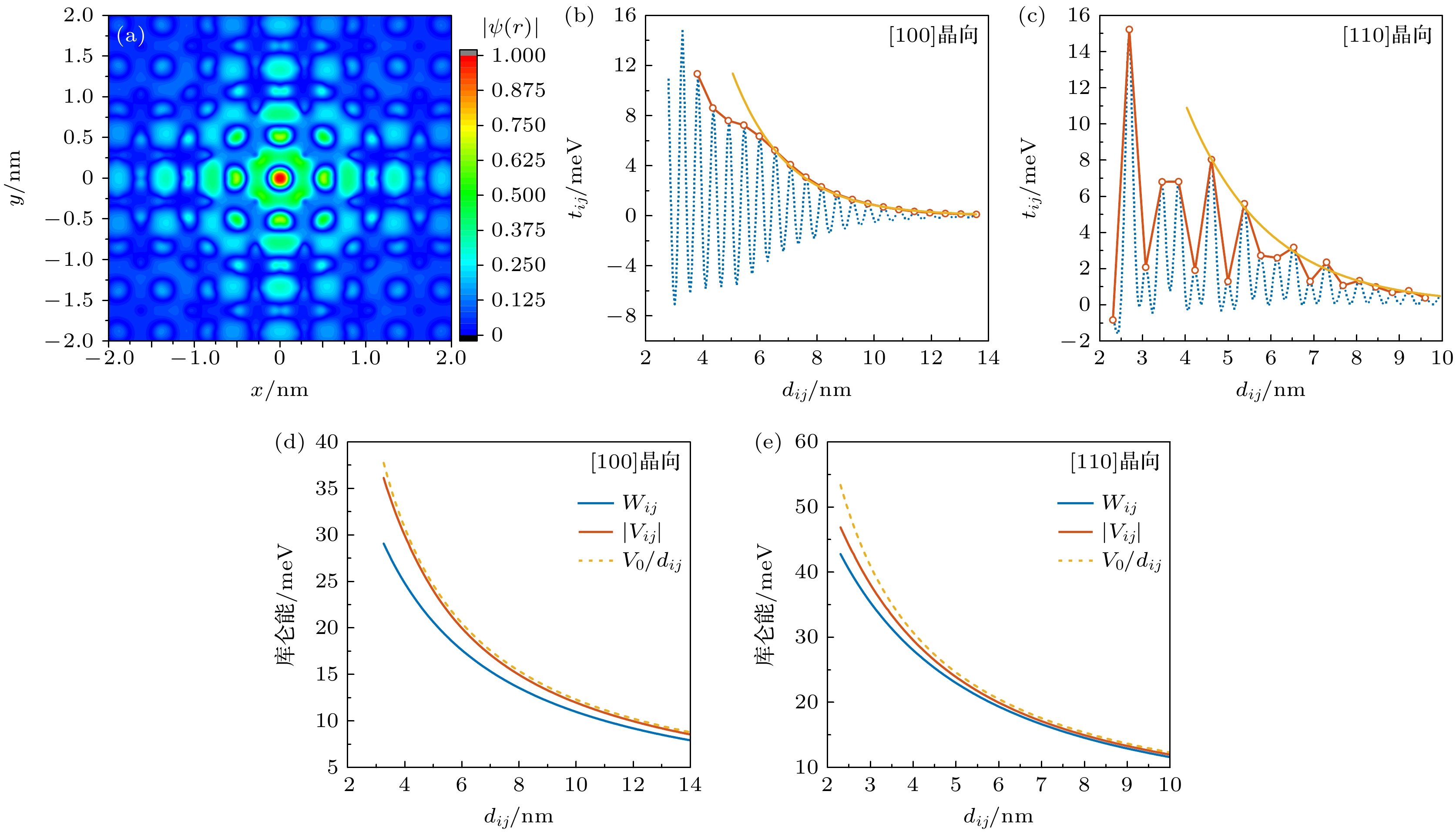
图 3 (a) 束缚在硅中孤立P杂质原子上的电子基态1sA1多谷耦合波函数; (b) [100]方向杂质原子耦合强度tij随杂质原子间间距dij的关系; (c) [110]方向杂质原子耦合强度tij随杂质原子间间距dij的关系; (d) [100]方向长程库仑吸引能Vij位间电子排斥能Wij随杂质原子间间距dij的关系; (e) [110]方向长程库仑吸引能Vij位间电子排斥能Wij随杂质原子间间距dij的关系
Fig. 3. (a) Multi-valley coupled wave function of the ground state 1sA1 for an electron bound to an isolated P dopant-induced in silicon; (b) coupling strength tij between dopant-induceds versus donor separation dij along the [100] crystal orientation; (c) coupling strength tij between dopant-induceds versus donor separation dij along the [110] crystal orientation; (d) long range Coulomb attraction Vij and inter-electron repulsion energy Wij versus donor separation dij along [100] crystal orientation; (e) long range Coulomb attraction Vij and inter-electron repulsion energy Wij versus donor separation dij along [110] crystal orientation.
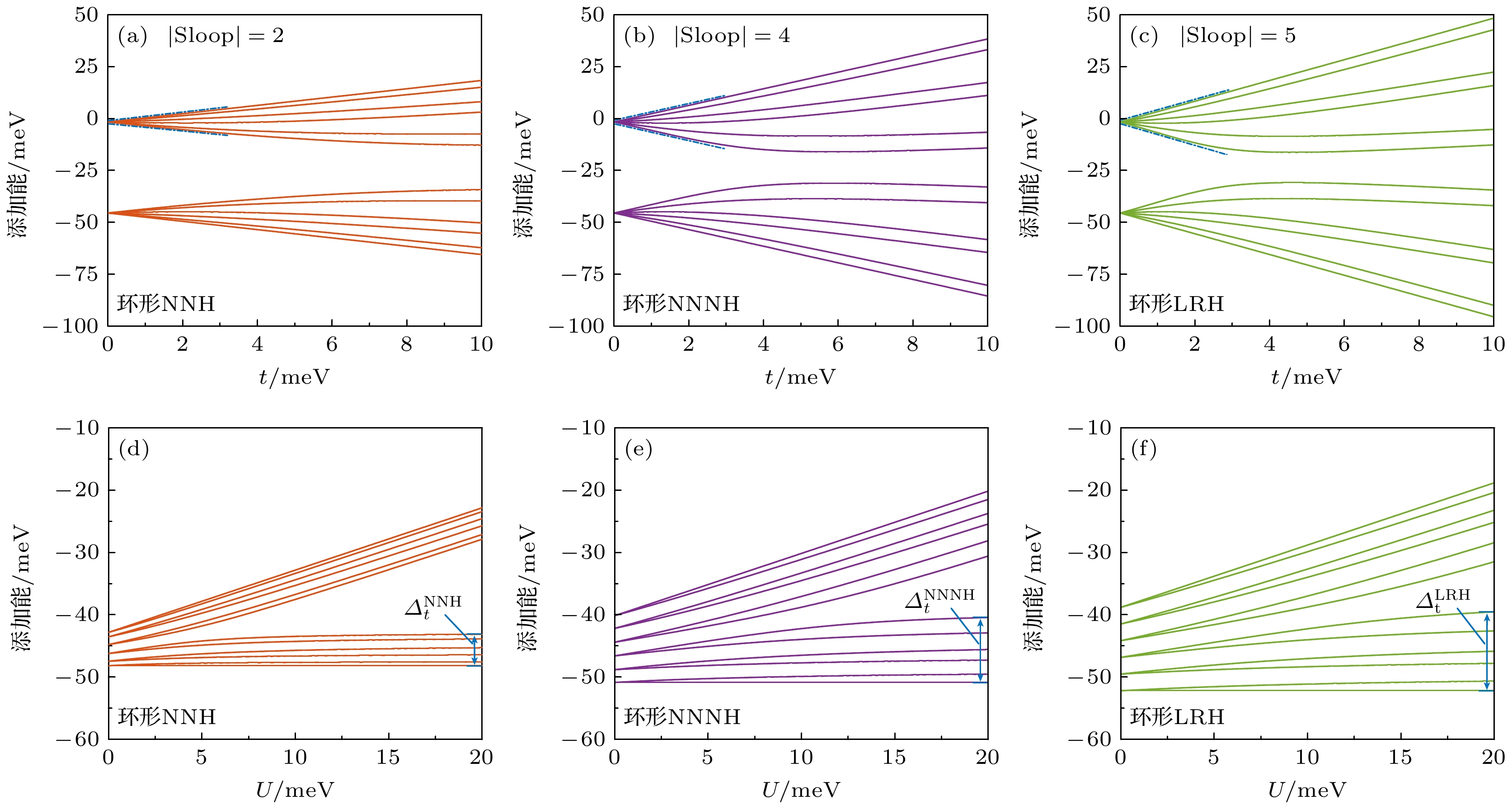
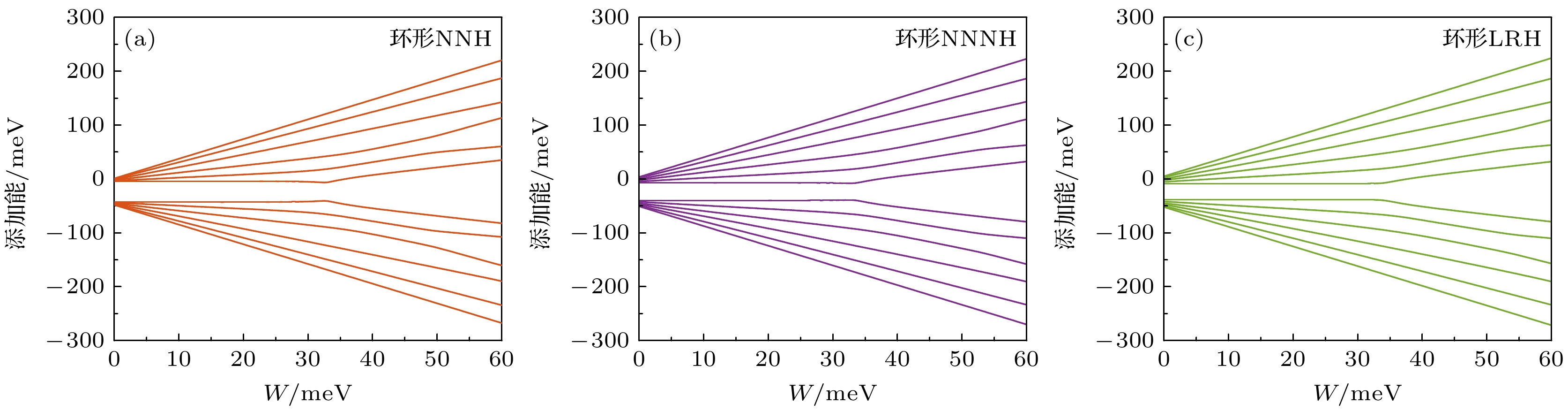
图 4 环形阵列($N = 6$)的电子添加能, 红色为NNH模型、紫色为NNNH模型、绿色为LRH模型 (a)—(c) 耦合强度对阵列电子添加能的影响($U = 43.86\ {\text{meV}}$); (d)—(f) 位间电子排斥能对于电子添加能的影响($t = 1.34\ {\text{meV}}$)
Fig. 4. Addition energy spectra of 6-sites annular array, calculated with: NNH model (red), NNNH model (purple), LRH model (green): (a)–(c) Impact of Coupling strength tij on addition energy spectra of the array; (d)–(f)impact of inter-site Coulomb interaction U on addition energy spectra.
图 5 最近邻库仑排斥能W对6位点环形阵列电子添加能谱的调制作用 (a) NNH模型; (b) NNNH模型; (c) LRH模型
Fig. 5. Modulation of addition energy spectra by nearest-neighbor Coulomb repulsion W in six-site annular array: (a) NNH model; (b) NNNH model; (c) LRH model.
图 6 电子排布重构临界点$\alpha $随位点数N的变化关系
Fig. 6. Relationship between electronic configuration reconstruction criticality.$\alpha $ with site number N
图 7 环形阵列中关联展宽系数$\beta $随位点数N的关系
Fig. 7. Site-number dependence of electron-correlation broadening coefficient $\beta $ in annular array.
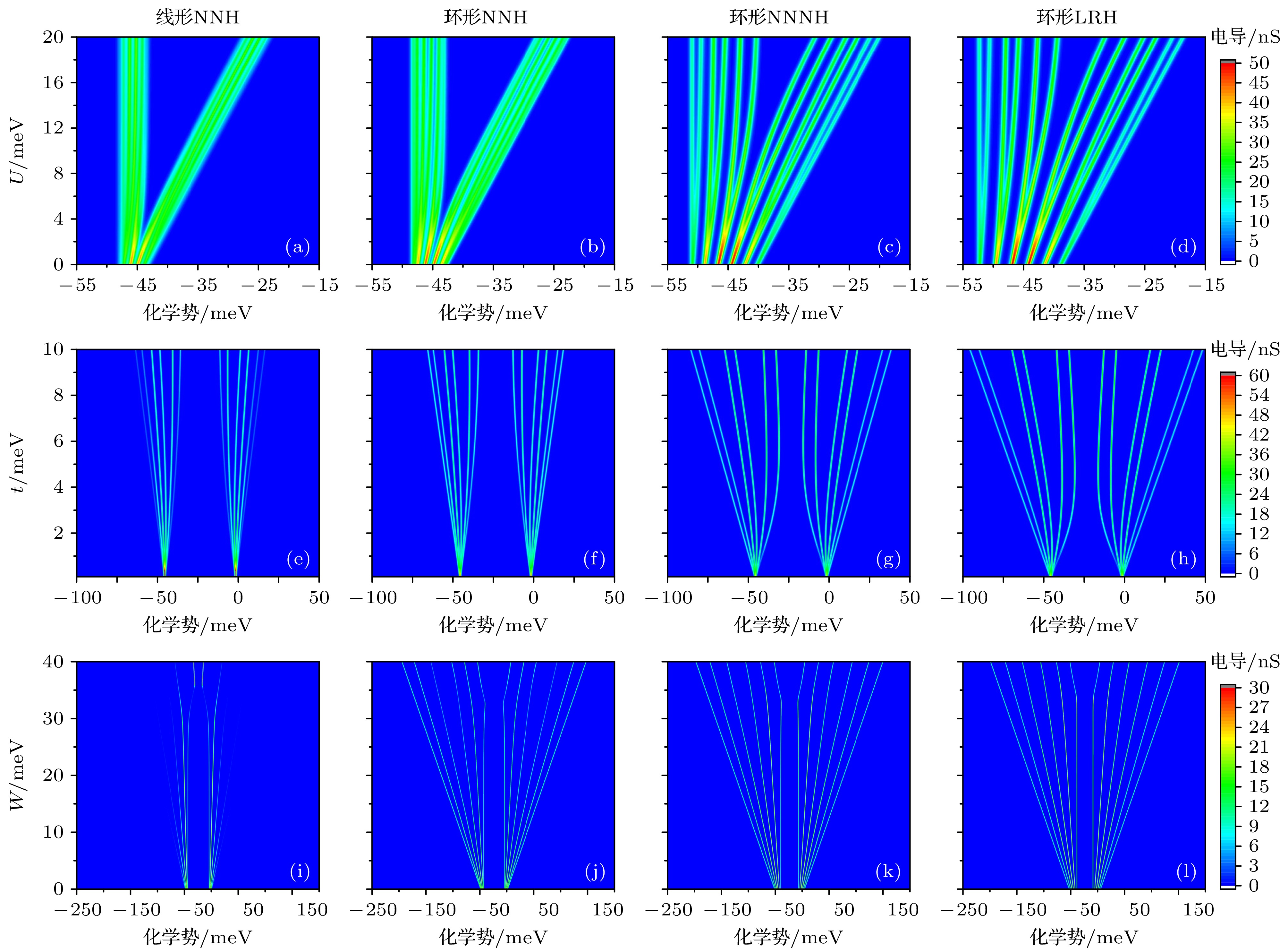
图 8 杂质原子阵列的电导特性对能量参数的响应规律 (a)—(d) 耦合强度t对电导特性的影响; (e)—(h) 在位电子排斥能U对电导特性的影响; (i)—(l) 最近邻位间电子排斥能W对电导特性的影响; (a), (e), (i) 仅存在最近邻跃迁的一维阵列; (b), (f), (j) NNH环形阵列; (c), (g), (k) NNNH环形阵列; (d), (h), (l) LRH环形阵列
Fig. 8. Response of conductance characteristics to energy parameters in dopant-induced arrays: (a)–(d) Conductance modulation by coupling strength t; (e)–(h) conductance modulation by on-site repulsion U; (i)–(l) conductance modulation by nearest-neighbor repulsion W; (a), (e), (i) 1D array (nearest-neighbor tunneling); (b), (f), (j) NNH annular array; (c), (g), (k) NNH annular array; (d), (h), (l) LRH annular array.
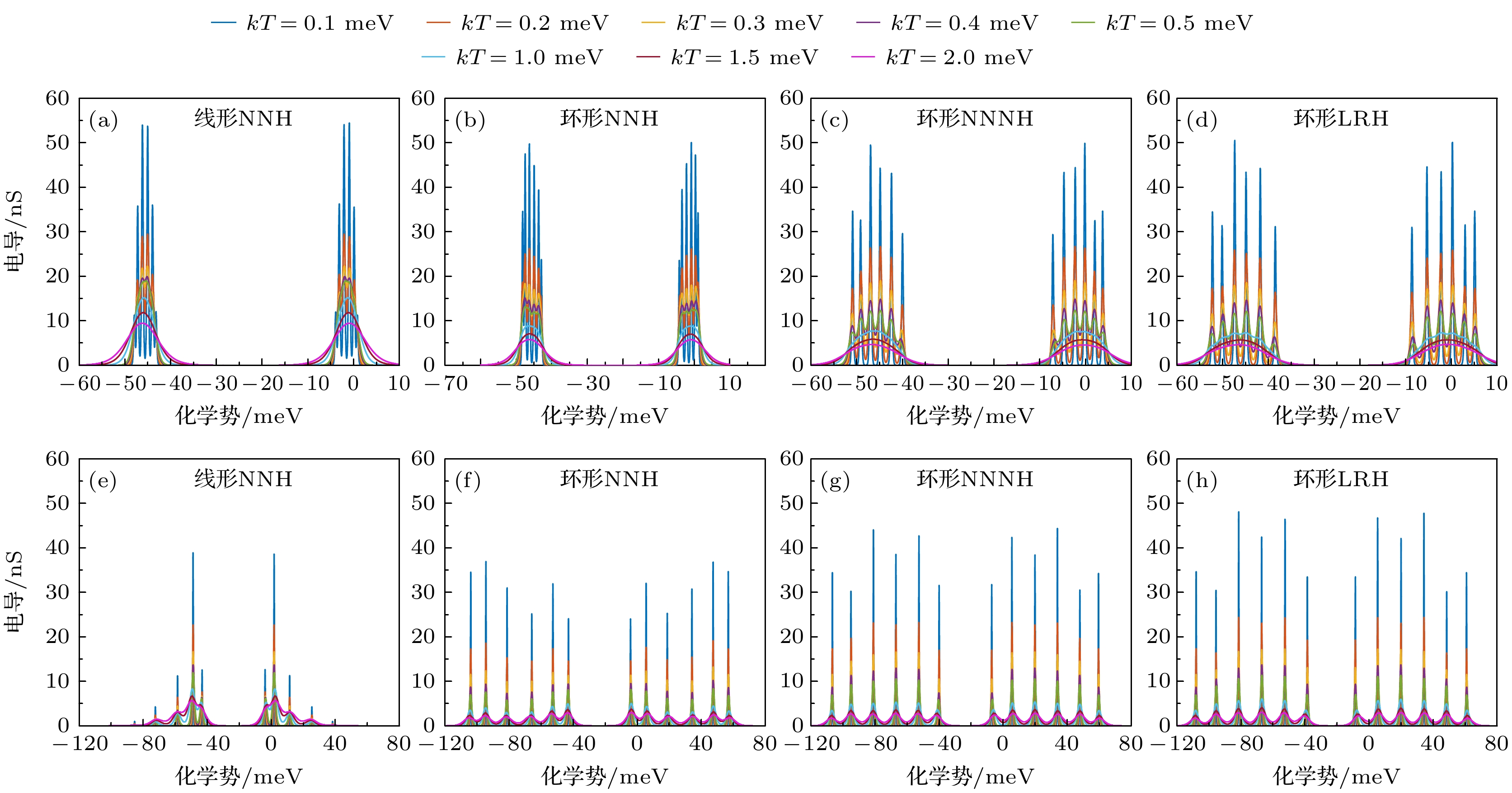
图 9 不同杂质原子阵列的温度依赖的电导特性 (a)—(d) 无位间电子排斥能和长程库仑吸引能体系; (e)—(h) 存在位间电子排斥能和长程库仑吸引能体系; (a), (e) 仅存在最近邻跃迁的一维阵列; (b), (f) NNH环形阵列; (c), (g) NNNH环形阵列; (d), (h) LRH环形阵列
Fig. 9. Temperature-dependent conductance characteristics in donor arrays: (a)–(d) Systems without inter-site repulsion Wij and long-range attraction Vij; (e)–(h) systems with inter-site repulsion Wij and long-range attraction Vij; (a), (e) 1D array (nearest-neighbor tunneling); (b), (f) NNH annular array; (c), (g) NNNH annular array; (d), (h) LRH annular array.
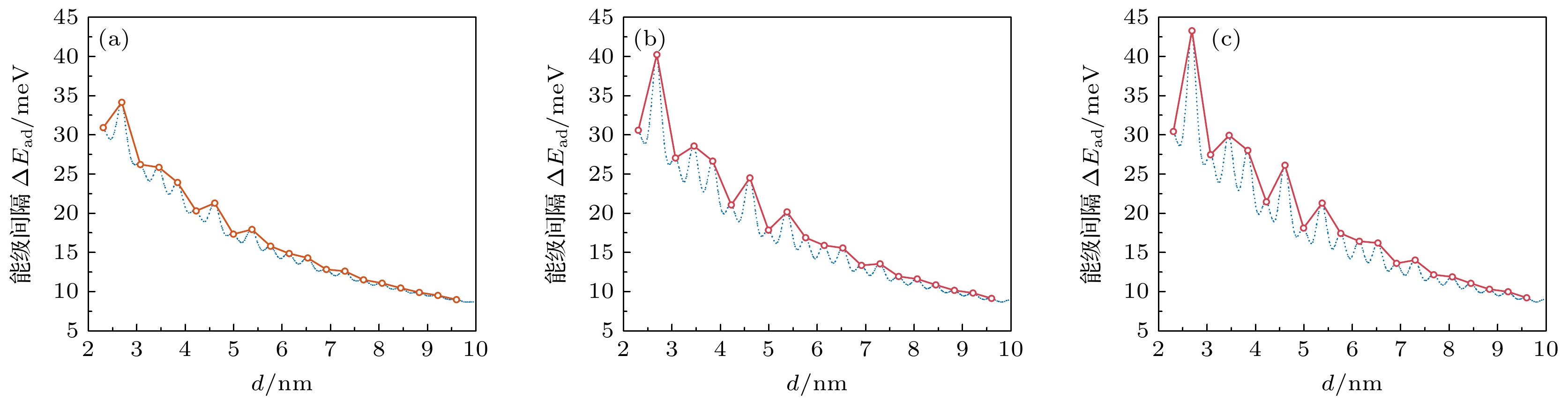
图 10 电子添加能能级间距(电导子峰间距)$\varDelta {E_{{\text{ad}}}}$随最近邻杂质原子间距d的变化关系 (a) NNH模型; (b) NNNH模型; (c) LRH模型
Fig. 10. Dependence of electron addition energy level $\varDelta {E_{{\text{ad}}}}$(corresponding to conductance sub-peak spacing) spacing on nearest-neighbor dopant-induced separation d: (a) NNH model; (b) NNNH model; (c) LRH model.
-
[1] Prati E, Hori M, Guagliardo F, Ferrari G, Shinada T 2012 Nat. Nanotechnol. 7 443
Google Scholar
[2] Wang X Q, Khatami E, Fei F, Wyrick J, Namboodiri P, Kashid R, Rigosi A F, Bryant G, Silver R 2022 Nat. Commun. 13 6824
Google Scholar
[3] Hubbard J 1963 Proc. Ro. Soc. London A 276 238
Google Scholar
[4] Beenakker C W J 1991 Phys. Rev. B 44 1646
Google Scholar
[5] Chen G, Klimeck G, Datta S, Chen G, Goddard W A 1994 Phys. Rev. B 50 8035
Google Scholar
[6] Yu Z M, Johnson A T, Heinzel T 1998 Phys. Rev. B 58 13830
Google Scholar
[7] Le N H, Fisher A J, Ginossar E 2017 Phys. Rev. B 96 245406
Google Scholar
[8] Wang S S, Li K, Dai Y M, Wang H H, Zhang Y C, Zhang Y Y 2023 Sci. Rep. 13 5763
Google Scholar
[9] Devi S, Ahluwalia P K, Chand S 2020 Pramana 94 60
Google Scholar
[10] Gamble J K, Jacobson N T, Nielsen E, Baczewski A D, Moussa J E, Montaño I, Muller R P 2015 Phys. Rev. B 91 235318
Google Scholar
[11] Hu X, Koiller B, Das Sarma S 2005 Phys. Rev. B 71 235332
Google Scholar
[12] Weber B, Mahapatra S, Ryu H, Lee S, Fuhrer A, Reusch T C G, Thompson D L, Lee W C T, Klimeck G, Hollenberg L C L, Simmons M Y 2012 Science 335 64
Google Scholar
[13] Voisin B, Bocquel J, Tankasala A, Usman M, Salfi J, Rahman R, Simmons M, Hollenberg L, Rogge S 2020 Nat. Commun. 11 6124
Google Scholar
[14] Slater J C, Koster G F 1954 Phys. Rev. 94 1498
Google Scholar
[15] Grzybowski P R, Chhajlany R W 2012 Phys. Status Solidi B 249 2231
Google Scholar
[16] Janod E, Tranchant J, Corraze B, Querré M, Stoliar P, Rozenberg M, Cren T, Roditchev D, Phuoc V T, Besland M P 2015 Adv. Funct. Mater. 25 6287
Google Scholar
[17] Morgan N Y, Abusch-Magder D, Kastner M A, Takahashi Y, Tamura H, Murase K 2001 J. Appl. Phys. 89 410
Google Scholar
[18] Cha M H, Hwang J 2020 Sci. Rep. 10 16701
Google Scholar
[19] Ochoa M A, Liu K, Zieliński M, Bryant G 2024 Phys. Rev. B 109 205412
Google Scholar
[20] Gerace D, Pavarini E, Andreani L C 2002 Phys. Rev. B 65 155331
Google Scholar
[21] Yi K S, Trivedi K, Floresca H C, Yuk H, Hu W, Kim M J 2011 Nano Lett. 11 5465
Google Scholar
下载:
计量
- 文章访问数: 351
- PDF下载量: 9
- 被引次数: 0
