-
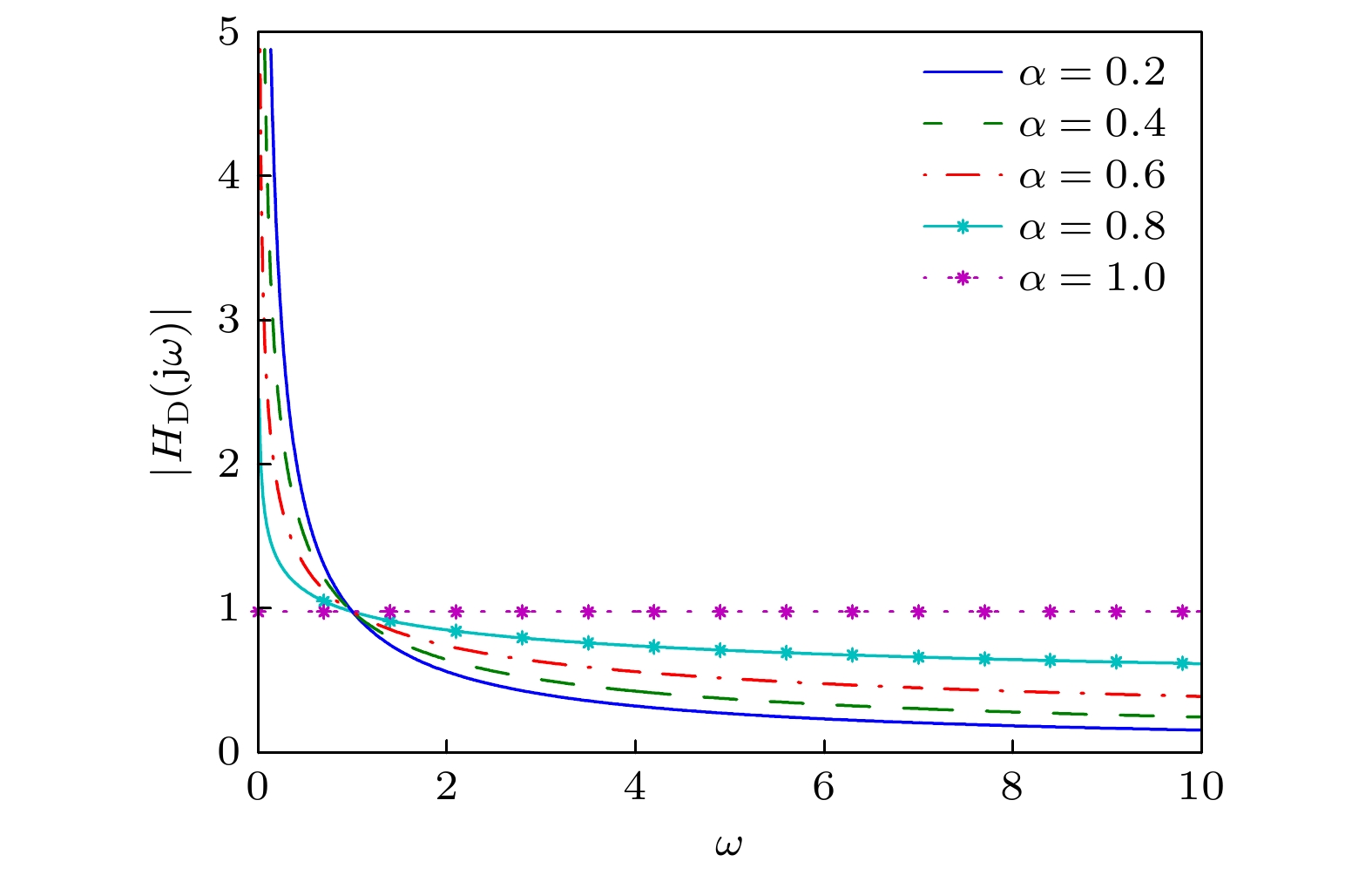
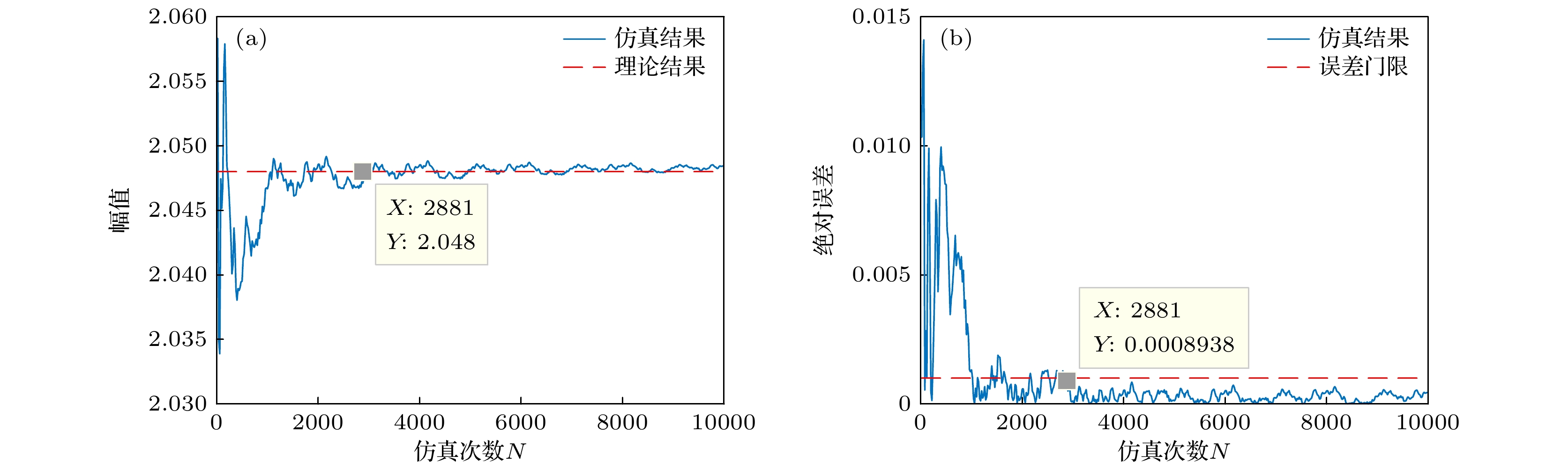
为了刻画在黏弹性介质中具有质量涨落的耦合粒子的运动行为, 本文提出了相应模型, 即三态噪声激励下的分数阶耦合系统. 利用Shapiro-Loginov公式和Laplace变换, 发现了粒子间的统计同步性, 并得到了系统输出幅值增益的解析表达. 在此基础上, 针对模型涉及的关键要素, 即耦合系统、分数阶系统和三态噪声, 着重分析了耦合系数、系统阶数和噪声稳态转移概率对系统输出幅值增益的广义随机共振现象的影响, 并给出了合理解释. 具体地说, 1)随着耦合系数的增大, 共振现象将先增强后减弱, 直至收敛. 该现象表明适当的耦合作用能够促进系统共振现象的产生, 体现了研究耦合系统的重要性. 2)随着系统阶数的增大, 共振现象将逐渐减弱. 当系统阶数取值为1, 即系统退化为整数阶系统时, 其输出幅值增益的峰值最小, 该现象说明分数阶系统能比传统整数阶系统得到更大的输出幅值增益. 3)噪声稳态转移概率对系统输出幅值增益的影响会随着与之相关的其他参数的变化而变化. 在一定参数条件下, 三态噪声不仅能够使系统输出幅值获得比双态噪声激励时更大的增益, 还能改变系统的共振类型. 最后, 通过数值仿真验证了上述结果的正确性.In order to describe the motion behavior of coupled particles with mass fluctuations in a viscous medium, we propose a corresponding model, namely a fractional-order coupled system excited by trichotomous noise. By using the Shapiro-Loginov formula and the Laplace transform, we find the statistical synchronization of the system, then obtain analytical expression of the system output amplitude gain. On this basis, this paper focuses on the key points, which are the coupled system, the fractional order system and the trichotomous noise, analyzes the influences of coupling coefficient, system order and noise steady-state probability on the generalized stochastic resonance phenomenon of system’s output amplitude gain, and gives some reasonable explanations. Specifically, first, as the coupling coefficient increases, the generalized stochastic resonance phenomenon of the output amplitude gain of the system first increases and then weakens until it converges. This phenomenon shows that the appropriate coupling strength can promote the generation of system resonance, thereby reflecting the importance of studying coupled systems. Second, with the order of the system increases, the generalized stochastic resonance phenomenon of the system’s output amplitude gain weakens gradually. When the system order value is 1, that is, when the system degenerates into an integer order system, the peak value of its output amplitude gain is smallest. This phenomenon shows that the fractional order system can obtain a larger output amplitude gain than the traditional integer order system. Third, the effect of the steady-state probability of noise on the output amplitude gain of the system changes with other related parameters. Under certain parameter conditions, trichotomous noise can not only make the output amplitude of the system larger than that of the system excited by dichotomous noise, but also change the resonance type of the system. Finally, the correctness of the above results is verified by numerical simulation.
-
Keywords:
- stochastic resonance /
- fractional system /
- coupled system /
- trichotomous noise
[1] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 L453
 Google Scholar
Google Scholar
[2] Wiesenfeld K, Moss F 1995 Nature 373 33
 Google Scholar
Google Scholar
[3] Gammaitoni L, Hänggi P, Jung P, Marchesoni F 1998 Rev. Mod. Phys. 70 223
 Google Scholar
Google Scholar
[4] Hänggi P 2002 Chem. Phys. Chem. 3 285
 Google Scholar
Google Scholar
[5] Zhang W, Xiang B R 2006 Talanta 70 267
 Google Scholar
Google Scholar
[6] Chen H, Varshney P K, Kay S M, Michels J H 2007 IEEE Trans. Signal Process. 55 3172
 Google Scholar
Google Scholar
[7] Soika E, Mankin R, Ainsaar A 2010 Phys. Rev. E 81 011141
 Google Scholar
Google Scholar
[8] Gang H, Ditzinger T, Ning C Z, Haken H 1993 Phys. Rev. Lett. 71 807
 Google Scholar
Google Scholar
[9] Pikovsky A, Zaikin A, Ma D L C 2002 Phys. Rev. Lett. 88 050601
 Google Scholar
Google Scholar
[10] Tessone C J, Mirasso C R, Toral R, Gunton J D 2006 Phys. Rev. Lett. 97 194101
 Google Scholar
Google Scholar
[11] 冷永刚, 王太勇, 郭焱, 吴振勇 2007 物理学报 56 30
 Google Scholar
Google Scholar
Leng Y G, Wang T Y, Guo Y, Wu Z Y 2007 Acta Phys. Sin. 56 30
 Google Scholar
Google Scholar
[12] 林敏, 黄咏梅, 方利民 2008 物理学报 57 2041
 Google Scholar
Google Scholar
Lin M, Huang Y M, Fang L M 2008 Acta Phys. Sin. 57 2041
 Google Scholar
Google Scholar
[13] 张莉, 刘立, 曹力 2010 物理学报 59 1494
 Google Scholar
Google Scholar
Zhang L, Liu L, Cao L 2010 Acta Phys. Sin. 59 1494
 Google Scholar
Google Scholar
[14] Berdichevsky V, Gitterman M 1999 Phys. Rev. E 60 1494
 Google Scholar
Google Scholar
[15] Yu T, Zhang L, Luo M K 2013 Phys. Scr. 88 045008
 Google Scholar
Google Scholar
[16] Zhong S C, Ma H, Peng H, Zhang L 2015 Nonlinear Dyn. 82 535
 Google Scholar
Google Scholar
[17] Yang B, Zhang X, Zhang L 2016 Phys. Rev. E 94 022119
[18] Lin L F, Yu L, Wang H Q 2017 Commun. Nonlinear Sci. Numer. Simul. 43 171
 Google Scholar
Google Scholar
[19] Zhang L, Lai L, Peng H 2018 Phys. Rev. E 97 012147
 Google Scholar
Google Scholar
[20] Yu T, Zhang L, Ji Y D, Lai L 2019 Commun. Nonlinear Sci. Numer. Simul. 72 26
 Google Scholar
Google Scholar
[21] Lin L F, Wang H Q 2019 Nonlinear Dyn. 98 801
 Google Scholar
Google Scholar
[22] 姜磊, 赖莉, 蔚涛, 罗懋康 2021 物理学报 70 130501
 Google Scholar
Google Scholar
Jiang L, Lai L, Yu T, Luo M K 2021 Acta Phys. Sin. 70 130501
 Google Scholar
Google Scholar
[23] Ausloos M, Lambiotte R 2006 Phys. Rev. E 73 011105
 Google Scholar
Google Scholar
[24] Gitterman M, Klyatskin V I 2010 Phys. Rev. E 81 051139
 Google Scholar
Google Scholar
[25] Gitterman M, Shapiro I 2011 J. Stat. Phys. 144 139
 Google Scholar
Google Scholar
[26] 蔚涛, 张路, 罗懋康 2013 物理学报 62 120504
 Google Scholar
Google Scholar
Yu T, Zhang L, Luo M K 2013 Acta Phys. Sin. 62 120504
 Google Scholar
Google Scholar
[27] 蔚涛, 罗懋康, 华云 2013 物理学报 62 210503
 Google Scholar
Google Scholar
Yu T, Luo M K, Hua Y 2013 Acta Phys. Sin. 62 210503
 Google Scholar
Google Scholar
[28] Broeck C V D 1983 J. Stat. Phys. 31 467
 Google Scholar
Google Scholar
[29] Zhong S C, Wei K, Gao S L, Ma H 2015 J. Stat. Phys. 159 195
 Google Scholar
Google Scholar
[30] Mankin R, Ainsaar A, Reiter E 1999 Phys. Rev. E 60 1374
 Google Scholar
Google Scholar
[31] Lang R L, Yang L, Qin H L, Di G H 2012 Nonlinear Dyn. 69 1423
 Google Scholar
Google Scholar
[32] Peng H, Ren R B, Li P F, Yu T 2020 Phys. Scr. 95 075214
 Google Scholar
Google Scholar
[33] Xu P F, Jin Y F 2020 Chaos, Solitons Fractals 138 109857
 Google Scholar
Google Scholar
[34] Jin Y F, Wang H Q 2020 Chaos, Solitons Fractals 133 109633
 Google Scholar
Google Scholar
[35] Jin Y F, Niu S Y 2016 Int. J. Mod. Phys. B 30 1650102
 Google Scholar
Google Scholar
[36] Bagley R L, Torvik P J 1984 Appl. Mech. 51 294
 Google Scholar
Google Scholar
[37] Lutz L 2001 Phys. Rev. E 64 051106
 Google Scholar
Google Scholar
[38] He G T, Tian Y, Wang Y 2013 J. Stat. Mech. 9 26
 Google Scholar
Google Scholar
[39] Jiang L, Lai L, Yu T, Luo M K 2021 J. Stat. Mech. 2021 063208
 Google Scholar
Google Scholar
[40] Cubero D 2008 Phys. Rev. E 77 021112
 Google Scholar
Google Scholar
[41] Tang Y, Zou W, Lu J, Kurths J 2012 Phys. Rev. E 85 046207
 Google Scholar
Google Scholar
[42] Atsumi Y, Hata S, Nakao H 2013 Phys. Rev. E 2013 88
 Google Scholar
Google Scholar
[43] Oyarzabal R S, Szezech Jr J D, Batista A M 2017 Commun. Nonlinear Sci. Numer. Simul. 54 62
 Google Scholar
Google Scholar
[44] Zhang L, Xu L, Yu T, Lai L, Zhong S C 2021 Commun. Nonlinear Sci. Numer. Simul. 93 105499
 Google Scholar
Google Scholar
[45] Shapiro V E, Loginov V M 1978 Phys. A 91 563
 Google Scholar
Google Scholar
-
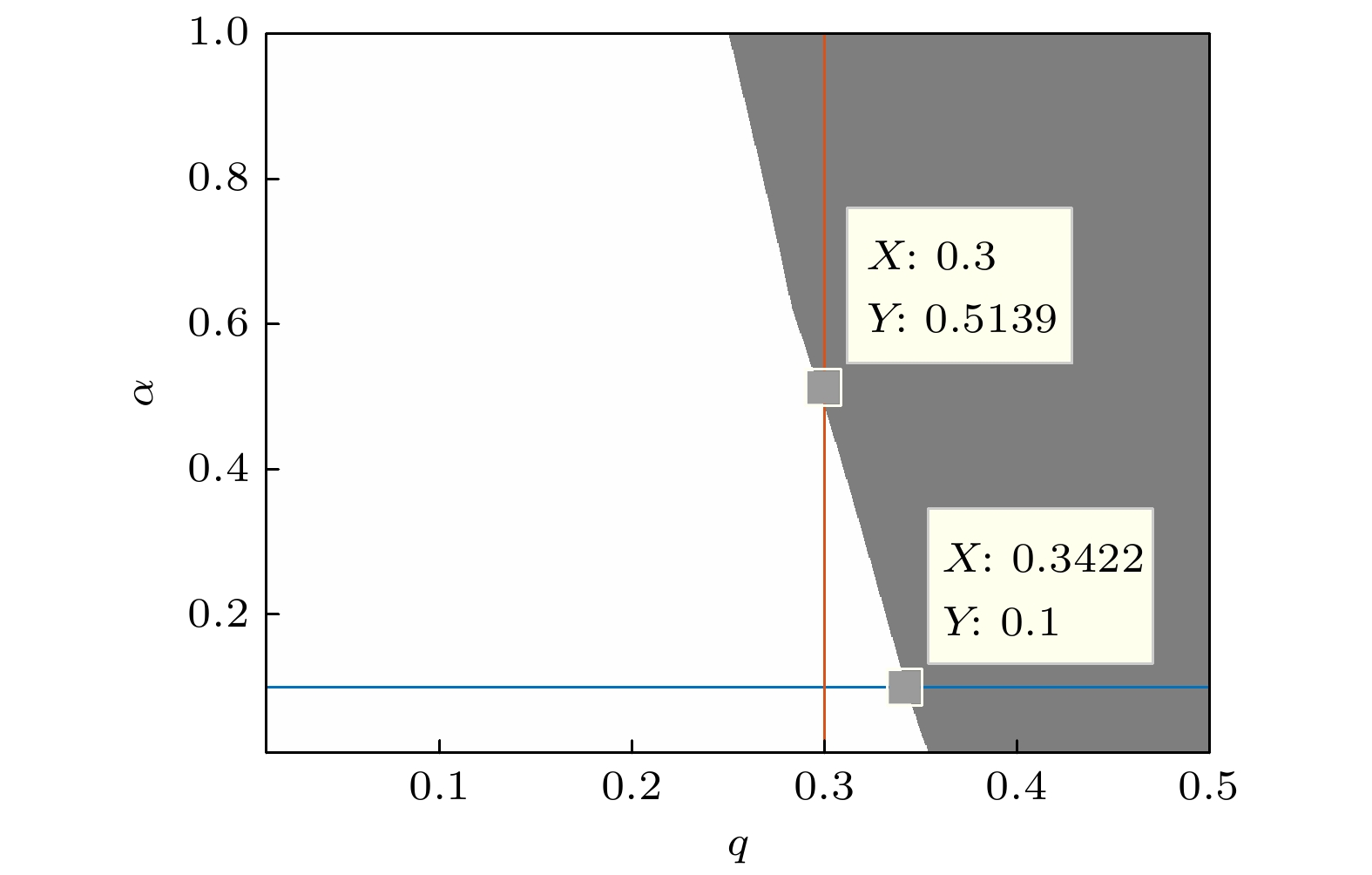
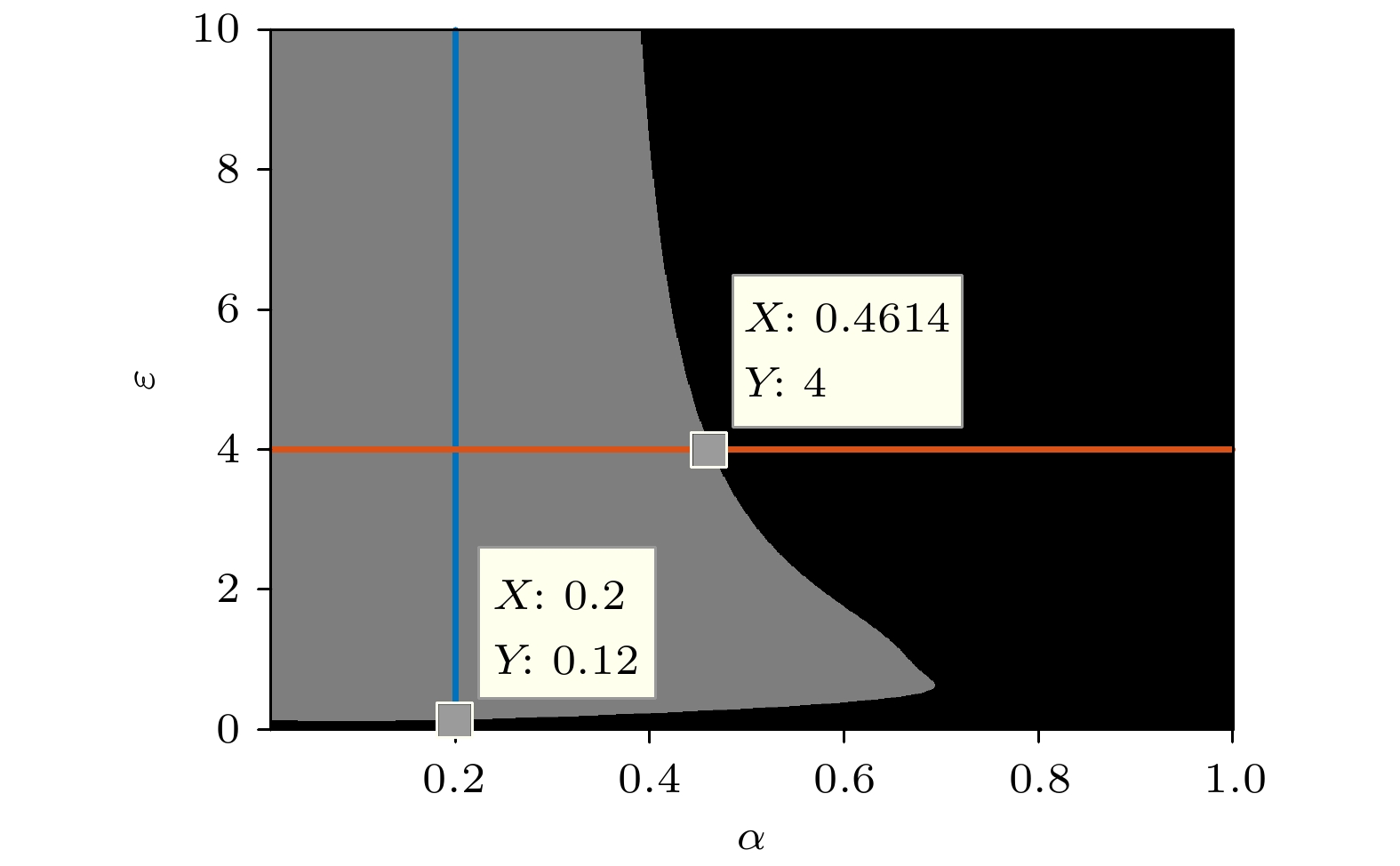
图 1 随q变化的GSR在
$\alpha\text{-}\varepsilon$ 平面的相图, 其中$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.4 $ ,$ \lambda=0.1 $ ,$ a=0.7 $ Fig. 1. Phase diagram for GSR versus q in the
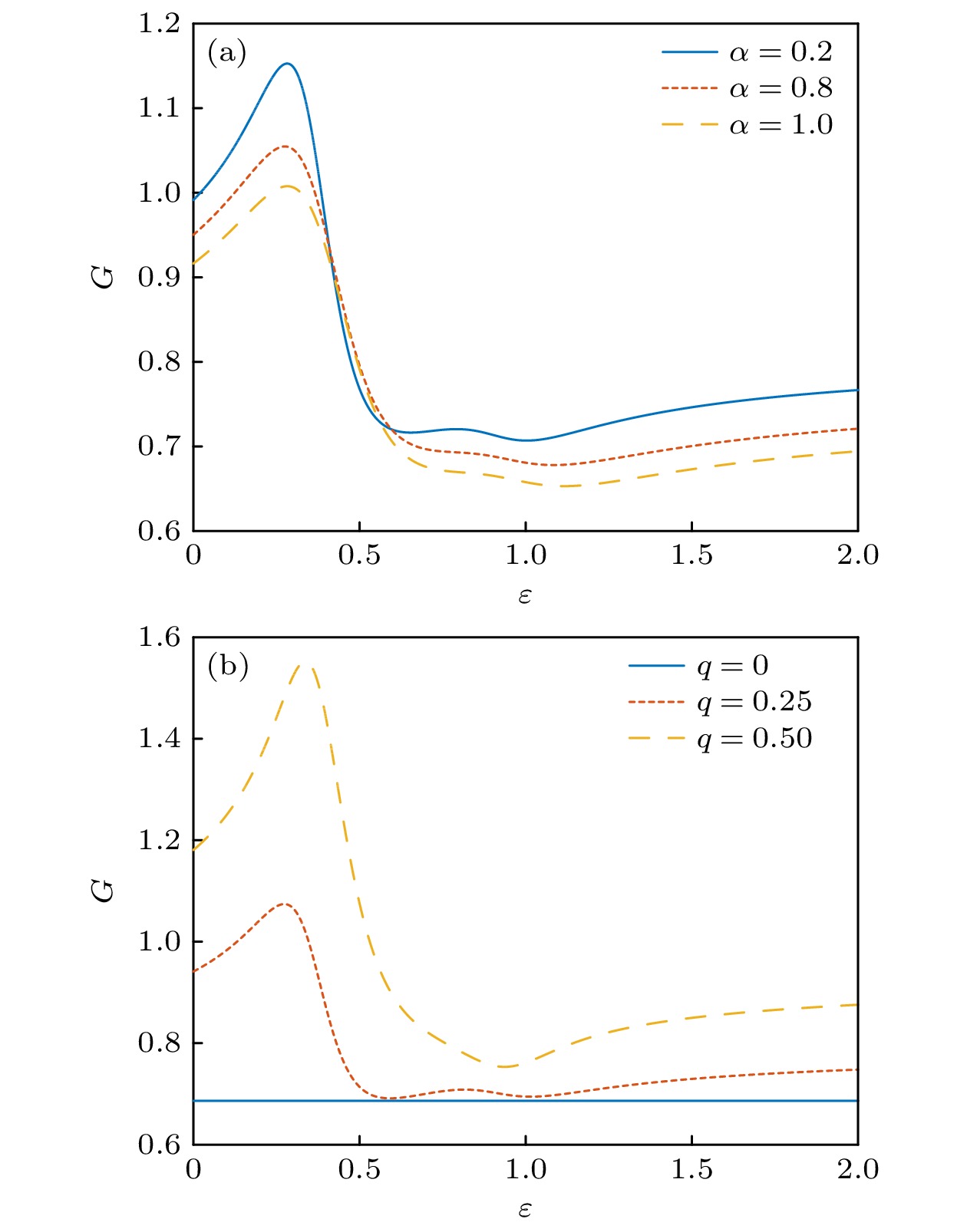
$\alpha\text{-}\varepsilon$ plane, with$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.4 $ ,$ \lambda=0.1 $ ,$ a=0.7 $ 图 2 系统输出幅值增益随噪声稳态转移概率q变化的GSR现象, 其中
$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.4 $ ,$ \lambda=0.1 $ ,$ a=0.7 $ (a)$ \varepsilon=4 $ ; (b)$ \alpha=0.2 $ Fig. 2. The OAG versus q with
$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.4 $ ,$ \lambda=0.1 $ ,$ a=0.7 $ : (a)$ \varepsilon=4 $ ; (b)$ \alpha=0.2 $ .图 5 系统输出幅值增益随耦合系数 ε变化的GSR现象, 其中
$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.6 $ ,$ \lambda=0.1 $ ,$ a=0.4 $ (a)$q= $ $ 0.3$ ; (b)$ \alpha=0.1 $ Fig. 5. The OAG versus ε with
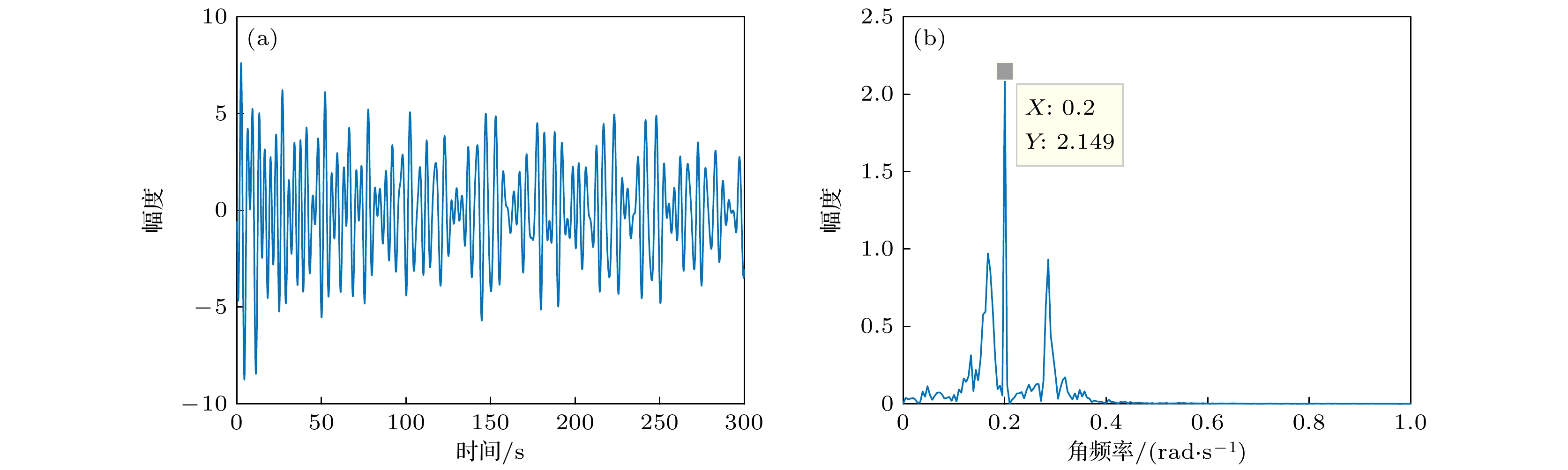
$ m=1 $ ,$ \gamma=0.1 $ ,$ \omega=1 $ ,$ \varOmega=1.6 $ ,$ \lambda=0.1 $ ,$ a=0.4 $ : (a)$ q=0.3 $ ; (b)$ \alpha=0.1 $ .图 6 系统输出信号 (a) 时域图; (b) 频域图.
$m = 1$ ,$\gamma = 0.1$ ,$\alpha = 0.5$ ,$\varepsilon = 1$ ,$\omega = 1$ ,$\varOmega = 0.4\pi$ ,$a = 0.2$ ,$\lambda = 0.1$ ,$q = 0.3$ Fig. 6. System output signal: (a) Time domain diagram; (b) frequency domain diagram.
$ m=1 $ ,$ \gamma=0.1 $ ,$ \alpha=0.5 $ ,$ \varepsilon=1 $ ,$ \omega=1 $ ,$ \varOmega=0.4\pi $ ,$ a=0.2 $ ,$ \lambda=0.1 $ ,$ q=0.3 $ . -
[1] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 L453
 Google Scholar
Google Scholar
[2] Wiesenfeld K, Moss F 1995 Nature 373 33
 Google Scholar
Google Scholar
[3] Gammaitoni L, Hänggi P, Jung P, Marchesoni F 1998 Rev. Mod. Phys. 70 223
 Google Scholar
Google Scholar
[4] Hänggi P 2002 Chem. Phys. Chem. 3 285
 Google Scholar
Google Scholar
[5] Zhang W, Xiang B R 2006 Talanta 70 267
 Google Scholar
Google Scholar
[6] Chen H, Varshney P K, Kay S M, Michels J H 2007 IEEE Trans. Signal Process. 55 3172
 Google Scholar
Google Scholar
[7] Soika E, Mankin R, Ainsaar A 2010 Phys. Rev. E 81 011141
 Google Scholar
Google Scholar
[8] Gang H, Ditzinger T, Ning C Z, Haken H 1993 Phys. Rev. Lett. 71 807
 Google Scholar
Google Scholar
[9] Pikovsky A, Zaikin A, Ma D L C 2002 Phys. Rev. Lett. 88 050601
 Google Scholar
Google Scholar
[10] Tessone C J, Mirasso C R, Toral R, Gunton J D 2006 Phys. Rev. Lett. 97 194101
 Google Scholar
Google Scholar
[11] 冷永刚, 王太勇, 郭焱, 吴振勇 2007 物理学报 56 30
 Google Scholar
Google Scholar
Leng Y G, Wang T Y, Guo Y, Wu Z Y 2007 Acta Phys. Sin. 56 30
 Google Scholar
Google Scholar
[12] 林敏, 黄咏梅, 方利民 2008 物理学报 57 2041
 Google Scholar
Google Scholar
Lin M, Huang Y M, Fang L M 2008 Acta Phys. Sin. 57 2041
 Google Scholar
Google Scholar
[13] 张莉, 刘立, 曹力 2010 物理学报 59 1494
 Google Scholar
Google Scholar
Zhang L, Liu L, Cao L 2010 Acta Phys. Sin. 59 1494
 Google Scholar
Google Scholar
[14] Berdichevsky V, Gitterman M 1999 Phys. Rev. E 60 1494
 Google Scholar
Google Scholar
[15] Yu T, Zhang L, Luo M K 2013 Phys. Scr. 88 045008
 Google Scholar
Google Scholar
[16] Zhong S C, Ma H, Peng H, Zhang L 2015 Nonlinear Dyn. 82 535
 Google Scholar
Google Scholar
[17] Yang B, Zhang X, Zhang L 2016 Phys. Rev. E 94 022119
[18] Lin L F, Yu L, Wang H Q 2017 Commun. Nonlinear Sci. Numer. Simul. 43 171
 Google Scholar
Google Scholar
[19] Zhang L, Lai L, Peng H 2018 Phys. Rev. E 97 012147
 Google Scholar
Google Scholar
[20] Yu T, Zhang L, Ji Y D, Lai L 2019 Commun. Nonlinear Sci. Numer. Simul. 72 26
 Google Scholar
Google Scholar
[21] Lin L F, Wang H Q 2019 Nonlinear Dyn. 98 801
 Google Scholar
Google Scholar
[22] 姜磊, 赖莉, 蔚涛, 罗懋康 2021 物理学报 70 130501
 Google Scholar
Google Scholar
Jiang L, Lai L, Yu T, Luo M K 2021 Acta Phys. Sin. 70 130501
 Google Scholar
Google Scholar
[23] Ausloos M, Lambiotte R 2006 Phys. Rev. E 73 011105
 Google Scholar
Google Scholar
[24] Gitterman M, Klyatskin V I 2010 Phys. Rev. E 81 051139
 Google Scholar
Google Scholar
[25] Gitterman M, Shapiro I 2011 J. Stat. Phys. 144 139
 Google Scholar
Google Scholar
[26] 蔚涛, 张路, 罗懋康 2013 物理学报 62 120504
 Google Scholar
Google Scholar
Yu T, Zhang L, Luo M K 2013 Acta Phys. Sin. 62 120504
 Google Scholar
Google Scholar
[27] 蔚涛, 罗懋康, 华云 2013 物理学报 62 210503
 Google Scholar
Google Scholar
Yu T, Luo M K, Hua Y 2013 Acta Phys. Sin. 62 210503
 Google Scholar
Google Scholar
[28] Broeck C V D 1983 J. Stat. Phys. 31 467
 Google Scholar
Google Scholar
[29] Zhong S C, Wei K, Gao S L, Ma H 2015 J. Stat. Phys. 159 195
 Google Scholar
Google Scholar
[30] Mankin R, Ainsaar A, Reiter E 1999 Phys. Rev. E 60 1374
 Google Scholar
Google Scholar
[31] Lang R L, Yang L, Qin H L, Di G H 2012 Nonlinear Dyn. 69 1423
 Google Scholar
Google Scholar
[32] Peng H, Ren R B, Li P F, Yu T 2020 Phys. Scr. 95 075214
 Google Scholar
Google Scholar
[33] Xu P F, Jin Y F 2020 Chaos, Solitons Fractals 138 109857
 Google Scholar
Google Scholar
[34] Jin Y F, Wang H Q 2020 Chaos, Solitons Fractals 133 109633
 Google Scholar
Google Scholar
[35] Jin Y F, Niu S Y 2016 Int. J. Mod. Phys. B 30 1650102
 Google Scholar
Google Scholar
[36] Bagley R L, Torvik P J 1984 Appl. Mech. 51 294
 Google Scholar
Google Scholar
[37] Lutz L 2001 Phys. Rev. E 64 051106
 Google Scholar
Google Scholar
[38] He G T, Tian Y, Wang Y 2013 J. Stat. Mech. 9 26
 Google Scholar
Google Scholar
[39] Jiang L, Lai L, Yu T, Luo M K 2021 J. Stat. Mech. 2021 063208
 Google Scholar
Google Scholar
[40] Cubero D 2008 Phys. Rev. E 77 021112
 Google Scholar
Google Scholar
[41] Tang Y, Zou W, Lu J, Kurths J 2012 Phys. Rev. E 85 046207
 Google Scholar
Google Scholar
[42] Atsumi Y, Hata S, Nakao H 2013 Phys. Rev. E 2013 88
 Google Scholar
Google Scholar
[43] Oyarzabal R S, Szezech Jr J D, Batista A M 2017 Commun. Nonlinear Sci. Numer. Simul. 54 62
 Google Scholar
Google Scholar
[44] Zhang L, Xu L, Yu T, Lai L, Zhong S C 2021 Commun. Nonlinear Sci. Numer. Simul. 93 105499
 Google Scholar
Google Scholar
[45] Shapiro V E, Loginov V M 1978 Phys. A 91 563
 Google Scholar
Google Scholar
计量
- 文章访问数: 6432
- PDF下载量: 105
- 被引次数: 0



























 下载:
下载: