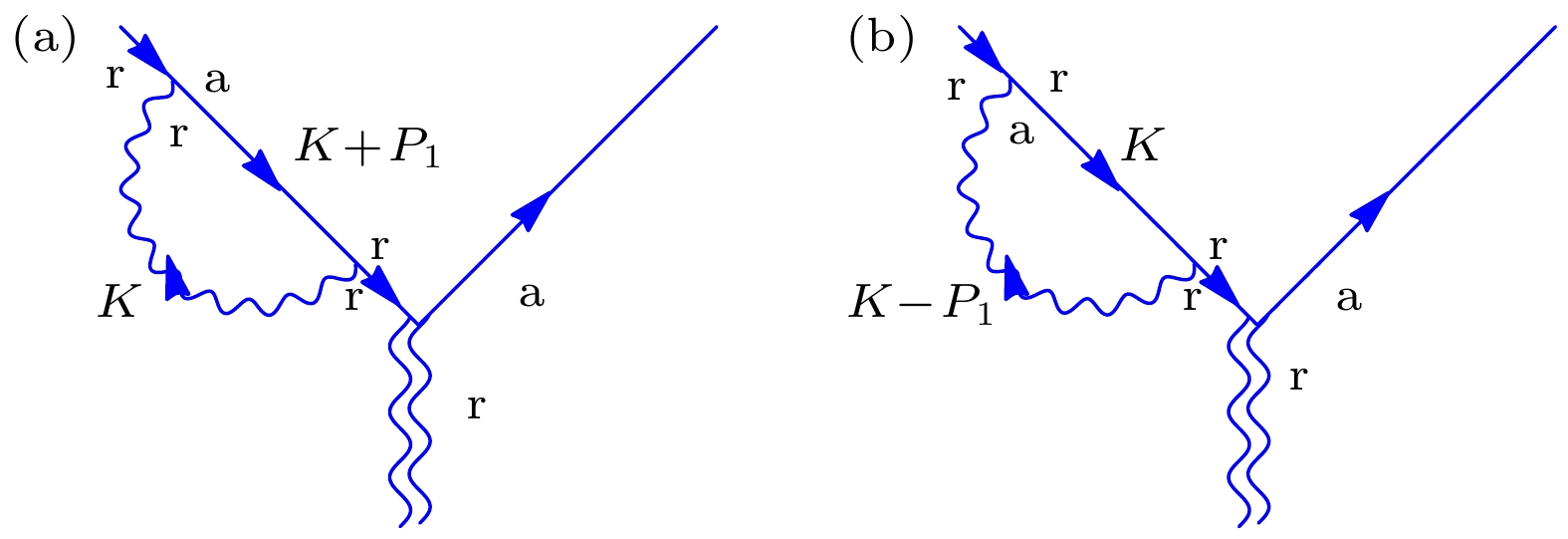
-
将引力形状因子推广到了手征费米子的情形, 并由此给出了熟知的自旋-涡旋耦合. 计算了量子电动力学等离子体中引力形状因子的辐射修正. 发现形状因子中存在两个结构对费米子在涡旋场中的散射振幅有贡献, 其中之一来自于费米子的自能修正, 指向介质中自旋-涡旋耦合的压低; 另一结构来自于对引力子-费米子顶点的修正, 这一修正不能解释为势能, 而是对应初末态的跃迁矩阵元. 两个结构均对手征涡旋效应产生贡献. 辐射修正总的效果是对手征涡旋效应的增强. 本文的结果从形状因子的角度澄清了自旋-涡旋耦合以及手征涡旋效应的联系和区别. 另外, 讨论了上述结果在量子色动力学等离子体中的应用, 结果暗示辐射修正可能对重离子碰撞的自旋极化现象有一定效应.We generalize the gravitational form factor for chiral fermion in vacuum, which reproduces the well-known spin-vorticity coupling. We also calculate radiative correction to the gravitational form factors in quantum electrodynamics plasma. We find two structures in the form factors contributing to the scattering amplitude of fermion in vorticity field, one is from the fermon self-energy correction, pointing to suppression of spin-vorticity coupling in medium; the other strucutre comes from graviton-fermion vertex correction, which does not adopt potential interpretation, but corresponds to transition matrix element between initial and final states. Both structures contribute to chiral vortical effect. The net effect is that radiative correction enhances the chiral vortical effect. Our results claify the relation and difference between spin-vorticity coupling and chiral vortical effect from the perspective of form factors. We also discuss the application of the results in QCD plasma, indicating radiative correction might have an appreciable effect in spin polarization effect in heavy ion collisions.
-
Keywords:
- gravitational form factor /
- spin-vorticity coupling /
- radiative correction /
- heavy ion collisions
[1] Adamczyk L, et al. 2017 Nature 548 62
[2] Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 [erratum: 2006 Phys. Rev. Lett. 96 039901]
[3] Liang Z T, Wang X N 2005 Phys. Lett. B 629 20
 Google Scholar
Google Scholar
[4] Gao J H, Chen S W, Deng W T, Liang Z T, Wang Q, Wang X N 2008 Phys. Rev. C 77 044902
 Google Scholar
Google Scholar
[5] Huang X G, Huovinen P, Wang X N 2011 Phys. Rev. C 84 054910
 Google Scholar
Google Scholar
[6] Jiang Y, Lin Z W, Liao J 2016 Phys. Rev. C 94 044910 [erratum: 2017 Phys. Rev. C 95 049904]
[7] Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90
 Google Scholar
Google Scholar
[8] Liu Y C, Huang X G 2020 Nucl. Sci. Tech. 31 56
 Google Scholar
Google Scholar
[9] Becattini F, Lisa M A 2020 Ann. Rev. Nucl. Part. Sci. 70 395
 Google Scholar
Google Scholar
[10] 孙旭, 周晨升, 陈金辉, 陈震宇, 马余刚, 唐爱洪, 徐庆华 2023 物理学报 72 072401
 Google Scholar
Google Scholar
Sun X, Zhou C S, Chen J H, Chen Z Y, Ma Y G, Tang A H, Xu Q H 2023 Acta Phys. Sin. 72 072401
 Google Scholar
Google Scholar
[11] 高建华, 黄旭光, 梁作堂, 王群, 王新年 2023 物理学报 72 072501
 Google Scholar
Google Scholar
Gao J H, Huang X G, Liang Z T, Wang Q, Wang X N 2023 Acta Phys. Sin. 72 072501
 Google Scholar
Google Scholar
[12] Becattini F, Karpenko I 2018 Phys. Rev. Lett. 120 012302
 Google Scholar
Google Scholar
[13] Wei D X, Deng W T, Huang X G 2019 Phys. Rev. C 99 014905
 Google Scholar
Google Scholar
[14] Fu B, Xu K, Huang X G, Song H 2021 Phys. Rev. C 103 024903
 Google Scholar
Google Scholar
[15] Adam J, et al. 2019 Phys. Rev. Lett. 123 132301
 Google Scholar
Google Scholar
[16] Liu S Y F, Yin Y 2021 JHEP 07 188
 Google Scholar
Google Scholar
[17] Becattini F, Buzzegoli M, Palermo A 2021 Phys. Lett. B 820 136519
 Google Scholar
Google Scholar
[18] Hidaka Y, Pu S, Yang D L 2018 Phys. Rev. D 97 016004
 Google Scholar
Google Scholar
[19] Fu B, Liu S Y F, Pang L, Song H, Yin Y 2021 Phys. Rev. Lett. 127 142301
 Google Scholar
Google Scholar
[20] Becattini F, Buzzegoli M, Inghirami G, Karpenko I, Palermo A 2021 Phys. Rev. Lett. 127 272302
 Google Scholar
Google Scholar
[21] Yi C, Pu S, Yang D L 2021 Phys. Rev. C 104 064901
 Google Scholar
Google Scholar
[22] Fu B, Pang L, Song H, Yin Y 2022 arXiv: 2201.12970 [hep-ph]
[23] Wu X Y, Yi C, Qin G Y, Pu S 2022 Phys. Rev. C 105 064909
 Google Scholar
Google Scholar
[24] Lin S, Wang Z 2022 JHEP 12 030
 Google Scholar
Google Scholar
[25] Liu Y C, Huang X G 2022 Sci. China Phys. Mech. Astron. 65 272011
 Google Scholar
Google Scholar
[26] Kobzarev I Y, Okun L B 1962 Zh. Eksp. Teor. Fiz. 43 1904
[27] Pagels H 1966 Phys. Rev. 144 1250
 Google Scholar
Google Scholar
[28] Donoghue J F, Holstein B R, Robinett R W 1984 Phys. Rev. D 30 2561
 Google Scholar
Google Scholar
[29] Donoghue J F, Holstein B R, Robinett R W 1985 Gen. Rel. Grav. 17 207
 Google Scholar
Google Scholar
[30] Buzzegoli M, Kharzeev D E 2021 Phys. Rev. D 103 116005
 Google Scholar
Google Scholar
[31] Hou D F, Liu H, Ren H C 2012 Phys. Rev. D 86 121703
 Google Scholar
Google Scholar
[32] Polyakov M V, Schweitzer P 2018 Int. J. Mod. Phys. A 33 1830025
 Google Scholar
Google Scholar
[33] Chen J Y, Son D T, Stephanov M A, Yee H U, Yin Y 2014 Phys. Rev. Lett. 113 182302
 Google Scholar
Google Scholar
[34] Hidaka Y, Pu S, Yang D L 2017 Phys. Rev. D 95 091901
 Google Scholar
Google Scholar
[35] Dong L, Lin S 2022 Eur. Phys. J. A 58 176
 Google Scholar
Google Scholar
[36] Hattori K, Hidaka Y, Yang D L 2019 Phys. Rev. D 100 096011
 Google Scholar
Google Scholar
[37] Weickgenannt N, Sheng X L, Speranza E, Wang Q, Rischke D H 2019 Phys. Rev. D 100 056018
 Google Scholar
Google Scholar
[38] Gao J H, Liang Z T 2019 Phys. Rev. D 100 056021
 Google Scholar
Google Scholar
[39] Liu Y C, Mameda K, Huang X G 2020 Chin. Phys. C 44 094101 [erratum: 2021 Chin. Phys. C 45 089001]
[40] Guo X 2020 Chin. Phys. C 44 104106
 Google Scholar
Google Scholar
[41] Chou K C, Su Z B, Hao B l, Yu L 1985 Phys. Rep. 118 1
 Google Scholar
Google Scholar
[42] Bellac M L 2011 Thermal Field Theory (Cambridge: Cambridge University Press) pp118–140
[43] Zhang C, Fang R H, Gao J H, Hou D F 2020 Phys. Rev. D 102 056004
 Google Scholar
Google Scholar
[44] Fang R H, Dong R D, Hou D F, Sun B D 2021 Chin. Phys. Lett. 38 091201
 Google Scholar
Google Scholar
[45] 赵新丽, 马国亮, 马余刚 2023 物理学报 Accepted
Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. Accepted
[46] Gao L L, Huang X G 2022 Chin. Phys. Lett. 39 021101
 Google Scholar
Google Scholar
[47] Abdallah M S, et al. 2023 Nature 614 7947
 Google Scholar
Google Scholar
[48] Wang X N 2023 Nucl. Sci. Tech. 34 15
 Google Scholar
Google Scholar
-
-
[1] Adamczyk L, et al. 2017 Nature 548 62
[2] Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 [erratum: 2006 Phys. Rev. Lett. 96 039901]
[3] Liang Z T, Wang X N 2005 Phys. Lett. B 629 20
 Google Scholar
Google Scholar
[4] Gao J H, Chen S W, Deng W T, Liang Z T, Wang Q, Wang X N 2008 Phys. Rev. C 77 044902
 Google Scholar
Google Scholar
[5] Huang X G, Huovinen P, Wang X N 2011 Phys. Rev. C 84 054910
 Google Scholar
Google Scholar
[6] Jiang Y, Lin Z W, Liao J 2016 Phys. Rev. C 94 044910 [erratum: 2017 Phys. Rev. C 95 049904]
[7] Gao J H, Ma G L, Pu S, Wang Q 2020 Nucl. Sci. Tech. 31 90
 Google Scholar
Google Scholar
[8] Liu Y C, Huang X G 2020 Nucl. Sci. Tech. 31 56
 Google Scholar
Google Scholar
[9] Becattini F, Lisa M A 2020 Ann. Rev. Nucl. Part. Sci. 70 395
 Google Scholar
Google Scholar
[10] 孙旭, 周晨升, 陈金辉, 陈震宇, 马余刚, 唐爱洪, 徐庆华 2023 物理学报 72 072401
 Google Scholar
Google Scholar
Sun X, Zhou C S, Chen J H, Chen Z Y, Ma Y G, Tang A H, Xu Q H 2023 Acta Phys. Sin. 72 072401
 Google Scholar
Google Scholar
[11] 高建华, 黄旭光, 梁作堂, 王群, 王新年 2023 物理学报 72 072501
 Google Scholar
Google Scholar
Gao J H, Huang X G, Liang Z T, Wang Q, Wang X N 2023 Acta Phys. Sin. 72 072501
 Google Scholar
Google Scholar
[12] Becattini F, Karpenko I 2018 Phys. Rev. Lett. 120 012302
 Google Scholar
Google Scholar
[13] Wei D X, Deng W T, Huang X G 2019 Phys. Rev. C 99 014905
 Google Scholar
Google Scholar
[14] Fu B, Xu K, Huang X G, Song H 2021 Phys. Rev. C 103 024903
 Google Scholar
Google Scholar
[15] Adam J, et al. 2019 Phys. Rev. Lett. 123 132301
 Google Scholar
Google Scholar
[16] Liu S Y F, Yin Y 2021 JHEP 07 188
 Google Scholar
Google Scholar
[17] Becattini F, Buzzegoli M, Palermo A 2021 Phys. Lett. B 820 136519
 Google Scholar
Google Scholar
[18] Hidaka Y, Pu S, Yang D L 2018 Phys. Rev. D 97 016004
 Google Scholar
Google Scholar
[19] Fu B, Liu S Y F, Pang L, Song H, Yin Y 2021 Phys. Rev. Lett. 127 142301
 Google Scholar
Google Scholar
[20] Becattini F, Buzzegoli M, Inghirami G, Karpenko I, Palermo A 2021 Phys. Rev. Lett. 127 272302
 Google Scholar
Google Scholar
[21] Yi C, Pu S, Yang D L 2021 Phys. Rev. C 104 064901
 Google Scholar
Google Scholar
[22] Fu B, Pang L, Song H, Yin Y 2022 arXiv: 2201.12970 [hep-ph]
[23] Wu X Y, Yi C, Qin G Y, Pu S 2022 Phys. Rev. C 105 064909
 Google Scholar
Google Scholar
[24] Lin S, Wang Z 2022 JHEP 12 030
 Google Scholar
Google Scholar
[25] Liu Y C, Huang X G 2022 Sci. China Phys. Mech. Astron. 65 272011
 Google Scholar
Google Scholar
[26] Kobzarev I Y, Okun L B 1962 Zh. Eksp. Teor. Fiz. 43 1904
[27] Pagels H 1966 Phys. Rev. 144 1250
 Google Scholar
Google Scholar
[28] Donoghue J F, Holstein B R, Robinett R W 1984 Phys. Rev. D 30 2561
 Google Scholar
Google Scholar
[29] Donoghue J F, Holstein B R, Robinett R W 1985 Gen. Rel. Grav. 17 207
 Google Scholar
Google Scholar
[30] Buzzegoli M, Kharzeev D E 2021 Phys. Rev. D 103 116005
 Google Scholar
Google Scholar
[31] Hou D F, Liu H, Ren H C 2012 Phys. Rev. D 86 121703
 Google Scholar
Google Scholar
[32] Polyakov M V, Schweitzer P 2018 Int. J. Mod. Phys. A 33 1830025
 Google Scholar
Google Scholar
[33] Chen J Y, Son D T, Stephanov M A, Yee H U, Yin Y 2014 Phys. Rev. Lett. 113 182302
 Google Scholar
Google Scholar
[34] Hidaka Y, Pu S, Yang D L 2017 Phys. Rev. D 95 091901
 Google Scholar
Google Scholar
[35] Dong L, Lin S 2022 Eur. Phys. J. A 58 176
 Google Scholar
Google Scholar
[36] Hattori K, Hidaka Y, Yang D L 2019 Phys. Rev. D 100 096011
 Google Scholar
Google Scholar
[37] Weickgenannt N, Sheng X L, Speranza E, Wang Q, Rischke D H 2019 Phys. Rev. D 100 056018
 Google Scholar
Google Scholar
[38] Gao J H, Liang Z T 2019 Phys. Rev. D 100 056021
 Google Scholar
Google Scholar
[39] Liu Y C, Mameda K, Huang X G 2020 Chin. Phys. C 44 094101 [erratum: 2021 Chin. Phys. C 45 089001]
[40] Guo X 2020 Chin. Phys. C 44 104106
 Google Scholar
Google Scholar
[41] Chou K C, Su Z B, Hao B l, Yu L 1985 Phys. Rep. 118 1
 Google Scholar
Google Scholar
[42] Bellac M L 2011 Thermal Field Theory (Cambridge: Cambridge University Press) pp118–140
[43] Zhang C, Fang R H, Gao J H, Hou D F 2020 Phys. Rev. D 102 056004
 Google Scholar
Google Scholar
[44] Fang R H, Dong R D, Hou D F, Sun B D 2021 Chin. Phys. Lett. 38 091201
 Google Scholar
Google Scholar
[45] 赵新丽, 马国亮, 马余刚 2023 物理学报 Accepted
Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. Accepted
[46] Gao L L, Huang X G 2022 Chin. Phys. Lett. 39 021101
 Google Scholar
Google Scholar
[47] Abdallah M S, et al. 2023 Nature 614 7947
 Google Scholar
Google Scholar
[48] Wang X N 2023 Nucl. Sci. Tech. 34 15
 Google Scholar
Google Scholar
计量
- 文章访问数: 9233
- PDF下载量: 184
- 被引次数: 0













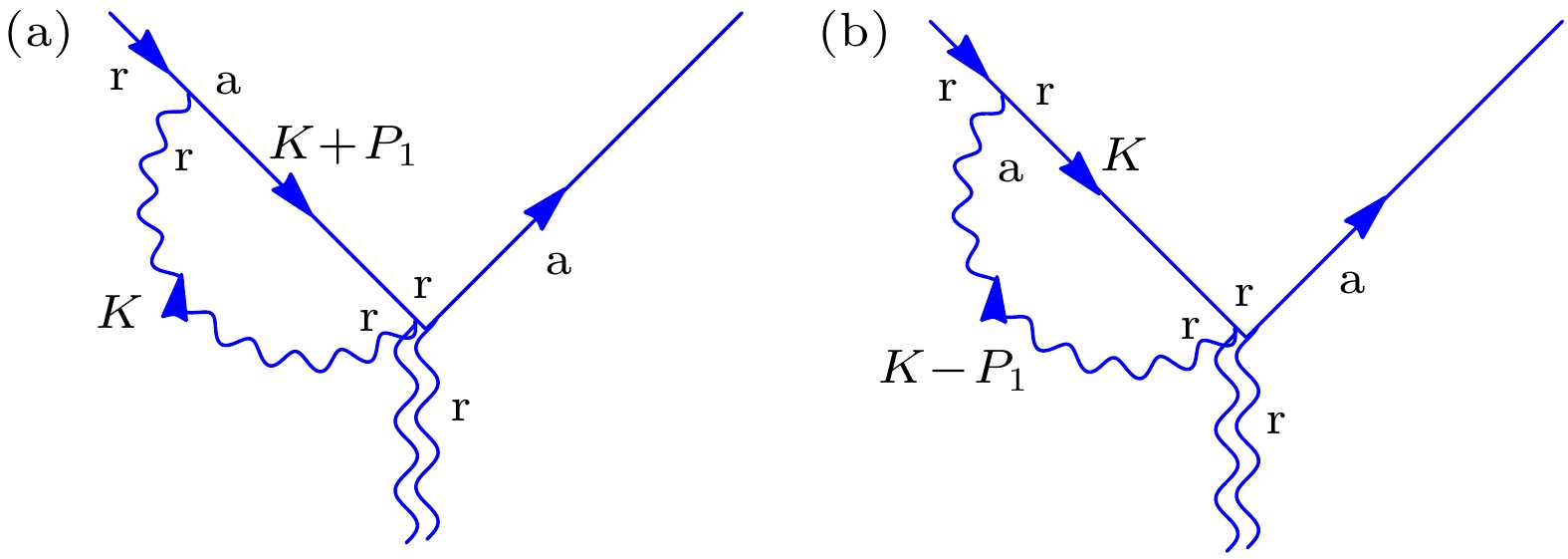
 下载:
下载: