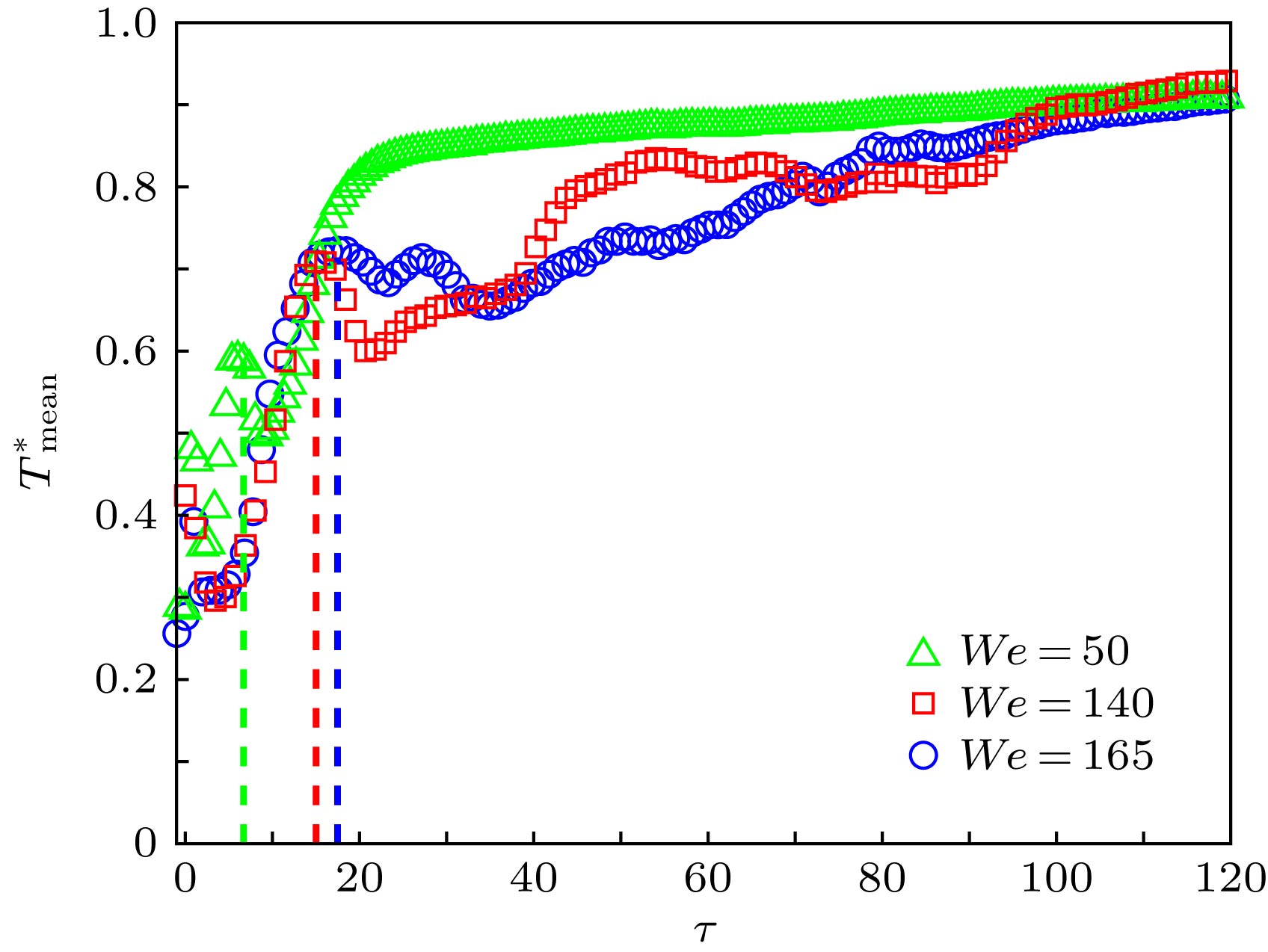
-
A high speed camera-infrared camera synchronous shoot device is built to record the process of cold droplet impacting on hot pool and lots of experiments have been done in this paper. The mixing morphology and the temperature variation of the impact area are observed and analyzed based on simultaneous images taken by the infrared camera and the high speed camera. The influences of the impact conditions on mixing and heat transfer during droplet impacting on hot pool are also studied and then the dimensionless relationship between mean temperature of the impact area and impact condition is established. The experimental results show that the mixing of cold liquid from droplet and hot pool is one of the main reasons for the temperature increase in impact area. The cold droplet does not integrate with hot pool immediately at the beginning of impact and the droplet is deformed into a shape of " crescent moon” which is trapped near the crater. The interface between cold liquid from droplet and hot pool can be observed in a simultaneous image. When the crater begins to collapse, the mixing liquid is mainly divided into two parts: one part is left and curled at the bottom of the pool while the other part is rising with the central jet. Despite the stagnation at the beginning, the mean temperature increases with time going by in the early stage. However the growth trend is interrupted by the cavity collapse. The mean temperature arrives at a peak after the crater has reached its maximum depth. The peak of the dimensionless temperature
$T_{{\rm{peak}}}^{\rm{*}}$ increases with the Weber number increasing and$T_{{\rm{peak}}}^{\rm{*}}$ can be described as$T_{{\rm{peak}}}^{\rm{*}} = 0.34W{e^{0.15}}$ . The dimensionless time of the peak${\tau _{{\rm{peak}}}}$ increases with the Froude number increasing. In this paper, we also find that the dimensionless time of the peak${\tau _{{\rm{peak}}}}$ can be described as${\tau _{{\rm{peak}}}} = 0.85F{r^{5/8}}$ . After the mean temperature reaches the peak, the growth trend presents a trend of fluctuations. The shape of the trend line during this stage is related to Weber number. When the Weber number is small, the growth trend of mean temperature decreases in a short period of time and then restores and increases with time going by. When the Weber number is bigger, the growth rate becomes smoother during the long fluctuation period. The mean temperature will increase very slowly at the end of the impact. Only some cold spot are left on the surface during this period and the rising of the mean temperature becomes steady and slow.-
Keywords:
- simultaneous images /
- droplet impact /
- hot pool /
- heat transfer
[1] Worthington A M, Cole R S 1897 Phil. Trans. Roy. Soc. 189 A137
Google Scholar
[2] Rein M 1993 Fluid Dyn. Res. 12 61
Google Scholar
[3] Rein M 1996 J. Fluid Mech. 306 150
[4] Yarin A L, Weiss D A 1995 J. Fluid Mech. 283 141
Google Scholar
[5] Cossali G E, Coghe A, Marengo M 1997 Exp. Fluids 22 465
[6] Roisman I V, Tropea C 2002 J. Fluid Mech. 472 373
Google Scholar
[7] Roisman I V, van Hinsberg N P, Tropea C 2008 Phys. Rev. E 77 046305
Google Scholar
[8] Bisighini A, Cossali G E, Tropea C 2010 Phys. Rev. E 82 036319
Google Scholar
[9] Mitchell A J, Simmons K, Hann D 2015 Proceedings of the ASME International Mechanical Engineering Congress and Exposition Houston, USA, Novemeber 13−19, 2015 pV001T01A038
[10] Mitchell A J, Hann D, Simmons K 2017 Proceedings of the ASME Turbo Expo Charlotte, USA June 26−30, 2017 pV02DT48A006
[11] Hann D B, Cherdantsev A V, Mitchell A 2016 Exp. Fluids 27 46
[12] Moreira A L N, Moita A S, Panao M R 2010 Prog. Energ. Combust 36 554
Google Scholar
[13] Bostanci H, Rini D P, Kizito J P 2012 Int. J. Heat Mass Transfer 55 3849
Google Scholar
[14] Zhang Z, Li J, Jiang P 2013 Appl. Therm. Eng. 51 102
Google Scholar
[15] Labergue A, Gradeck M, Lemoine F 2015 Int. J. Heat Mass Transfer 81 889
Google Scholar
[16] Bernardin J, Stebbins C, Mudawar I 1997 Int. J. Heat Mass Transfer 40 247
Google Scholar
[17] Pasandideh-Fard M, Aziz S, Chandra S, Mostaghimi J 2001 Int. J. Heat Fluid Flow 22 201
Google Scholar
[18] Castanet G, Liénart T, Lemoine F 2009 Int. J. Heat Mass Transfer 52 670
Google Scholar
[19] 叶学民, 李永康, 李春曦 2016 物理学报 65 234701
Google Scholar
Ye X M, Li Y K, Li C X 2016 Acta Phys. Sin. 65 234701
Google Scholar
[20] Gao X, Kong L, Li R 2017 Int. J. Heat Mass Transfer 108 1068
Google Scholar
[21] Liang G, Mu X, Guo Y 2016 Numer. Heat Tr. B: Fund 69 575
Google Scholar
-
图 1 冷液滴/热液池碰撞实验装置构成图
Figure 1. Experimental schematic diagram.
图 2 冷液滴/热液池碰撞过程的高速摄像及红外摄像同步时序图 i)高速摄像图片; ii)红外摄像图片
Figure 2. The simultaneous images of droplet impacting on hot pool: i) Images taken from high speed camera; ii) images taken from infrared camera.
图 3 冷液滴/热液池碰撞过程的侧面红外摄像图 (a) t = 50.0 ms; (b) t = 60.0 ms
Figure 3. The side view of droplet impacting on hot pool: (a) t = 50.0 ms; (b) t = 60.0 ms.
图 4 径向温度分布和温度分布直方图随时间的变化 (a) 径向温度分布随碰撞时间的变化; (b) 温度分布直方图随时间的变化
Figure 4. The radical temperature profile and the temperature histogram of the impacting area: (a) The radical temperature profile; (b) the temperature histogram of the impacting area.
图 5 三种韦伯数条件下无量纲平均温度随时间的变化规律
Figure 5. The non-dimensional mean temperature as a function of dimensionless time.
图 6 无量纲平均温度极值点的温度值、出现时间与工况条件的关系 (a)无量纲平均温度极值点的温度值; (b)无量纲平均温度极值点的出现时间
Figure 6. The peak of dimensionless temperature and the dimensionless time of the peak: (a) The peak of dimensionless temperature as a function of Weber number; (b) the dimensionless time of the peak as a function of Froude number.
-
[1] Worthington A M, Cole R S 1897 Phil. Trans. Roy. Soc. 189 A137
Google Scholar
[2] Rein M 1993 Fluid Dyn. Res. 12 61
Google Scholar
[3] Rein M 1996 J. Fluid Mech. 306 150
[4] Yarin A L, Weiss D A 1995 J. Fluid Mech. 283 141
Google Scholar
[5] Cossali G E, Coghe A, Marengo M 1997 Exp. Fluids 22 465
[6] Roisman I V, Tropea C 2002 J. Fluid Mech. 472 373
Google Scholar
[7] Roisman I V, van Hinsberg N P, Tropea C 2008 Phys. Rev. E 77 046305
Google Scholar
[8] Bisighini A, Cossali G E, Tropea C 2010 Phys. Rev. E 82 036319
Google Scholar
[9] Mitchell A J, Simmons K, Hann D 2015 Proceedings of the ASME International Mechanical Engineering Congress and Exposition Houston, USA, Novemeber 13−19, 2015 pV001T01A038
[10] Mitchell A J, Hann D, Simmons K 2017 Proceedings of the ASME Turbo Expo Charlotte, USA June 26−30, 2017 pV02DT48A006
[11] Hann D B, Cherdantsev A V, Mitchell A 2016 Exp. Fluids 27 46
[12] Moreira A L N, Moita A S, Panao M R 2010 Prog. Energ. Combust 36 554
Google Scholar
[13] Bostanci H, Rini D P, Kizito J P 2012 Int. J. Heat Mass Transfer 55 3849
Google Scholar
[14] Zhang Z, Li J, Jiang P 2013 Appl. Therm. Eng. 51 102
Google Scholar
[15] Labergue A, Gradeck M, Lemoine F 2015 Int. J. Heat Mass Transfer 81 889
Google Scholar
[16] Bernardin J, Stebbins C, Mudawar I 1997 Int. J. Heat Mass Transfer 40 247
Google Scholar
[17] Pasandideh-Fard M, Aziz S, Chandra S, Mostaghimi J 2001 Int. J. Heat Fluid Flow 22 201
Google Scholar
[18] Castanet G, Liénart T, Lemoine F 2009 Int. J. Heat Mass Transfer 52 670
Google Scholar
[19] 叶学民, 李永康, 李春曦 2016 物理学报 65 234701
Google Scholar
Ye X M, Li Y K, Li C X 2016 Acta Phys. Sin. 65 234701
Google Scholar
[20] Gao X, Kong L, Li R 2017 Int. J. Heat Mass Transfer 108 1068
Google Scholar
[21] Liang G, Mu X, Guo Y 2016 Numer. Heat Tr. B: Fund 69 575
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7262
- PDF Downloads: 67
- Cited By: 0
