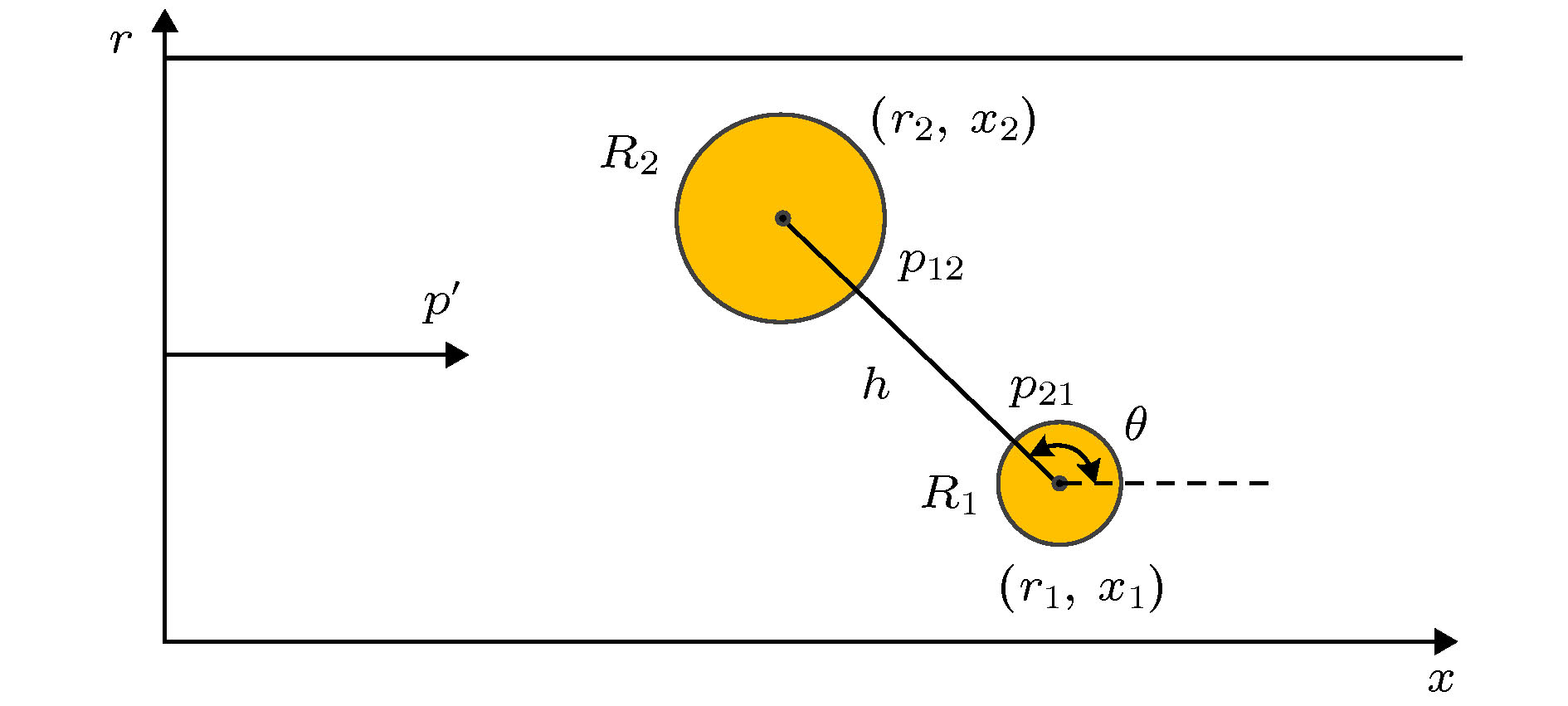
-
Acoustically-excited bubble dynamics is the foundation of pipeline bubble detection based on acoustic technology. Due to the existence of multiple bubbles in pipeline flow, the Bjerknes forces among arbitrary bubbles under acoustic excitation may enforce bubble-bubble interaction and then change the features of bubble dynamics. Based on traditional free bubble’s Rayleigh-Plesset (R-P) model, this paper tries to establish bubble-bubble interaction model in consideration of the second Bjerknes force and bubble distribution in the pipeline axial direction. Meanwhile, the influence of finite wave speed in compressible fluid is considered. The proposed model is numerically calculated by the fourth-order Runge-Kutta method. Firstly, the differences in bubble feature between the free bubble’s R-P model and bubble-bubble interaction model are compared under excitation with different frequencies and amplitudes. Results show that the differences in bubble dynamics are minor when the bubble’s distance is large enough. When the bubble’s distance is fixed, the differences are significant on condition that the frequency of acoustic excitation is nearly the resonant frequency of bubbles. Secondly, through establishing compressible model and incompressible fluid model, we compare the differences between the two models. Numerical calculations show that the second Bjerknes force under the compressible assumption acts as an external force and forces the bubble to vibrate. On the other hand, the second Bjerknes force under the incompressible assumption changes the dynamics of bubble-bubble interaction as well as the resonant features. Finally, we study the effect of bubble-bubble distance and bubble’s axial position on bubble vibration characteristics. The bubble-bubble distance affects the second Bjerknes force and may lead the bubbles to vibrate nonlinearly. The bubble’s axial position changes the phase of external acoustic force and leads to the difference in initial vibration feature. When this difference is coupled with the second Bjerknes force, the bubble-bubble interaction may be changed even into nonlinear vibration, leading the bubble’s oscillation spectrum to differ from linear vibrations significantly. These results demonstrate that the resonant state of a small bubble may be converted into nonlinear vibration state if the second Bjerknes force is present. On the other hand, the resonant state of a large bubble can keep linear vibration when the second Bjerknes force is not obvious.
-
Keywords:
- bubble dynamics /
- second Bjerknes force /
- compressible fluid /
- bubble detection
[1] Balasubramaniam R, Ramé E, Motil B J 2019 Case Western Reserve University Cleveland, Ohio NASA Report No. 20190001795
[2] Wen W, Zong G, Bi S 2014 Rev. Sci. Instrum. 85 065106
Google Scholar
[3] Leighton T G, Ramble D G, Phelps A D 1997 J. Acoust. Soc. Am. 101 2626
Google Scholar
[4] Leighton T G, Baik K, Jiang J 2012 Proc. R. Soc. London, Ser. A 468 2461
Google Scholar
[5] Hsieh D, Plesset M S 1961 Phys. Fluids 4 970
Google Scholar
[6] Sangani A S, Sureshkumar R 1993 J. Fluid Mech. 252 239
Google Scholar
[7] Kerboua K, Hamdaoui O 2019 J. Acoust. Soc. Am. 146 2240
Google Scholar
[8] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 75 046304
Google Scholar
[9] Jang N W, Gracewski S I, Abrahamsen B, Buttaccio T, Halm R 2009 J. Acoust. Soc. Am. 126 EL34
Google Scholar
[10] Prosperetti A 1974 J. Acoust. Soc. Am. 56 878
Google Scholar
[11] Feng Z C, Leal L G 1997 Ann. Rev. Fluid Mech. 29 201
Google Scholar
[12] Lauterborn W, Kurz T 2010 Rep. Prog. Phys. 73 106501
Google Scholar
[13] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[14] Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924
Google Scholar
[15] Pelekasis N A, Gaki A, Doinikov A, Tsamopoulos J A 2004 J. Fluid Mech. 500 313
Google Scholar
[16] Liang J, Wang X, Yang J, Gong L 2017 Ultrasonics 75 58
Google Scholar
[17] Omta R 1987 J. Acoust. Soc. Am. 82 1018
Google Scholar
[18] Hamilton M F, Ilinskii Y A, Meegan G D, Zabolotskaya E A 2005 Acoust. Res. Lett. Online 6 207
Google Scholar
[19] Doinikov A A 2004 J. Acoust. Soc. Am. 116 821
Google Scholar
[20] Maiga M A, Coutier-Delgosha O, Buisine D 2018 Phys. Fluids 30 123301
Google Scholar
[21] Yoshida K, Fujikawa T, Watanabe Y 2011 J. Acoust. Soc. Am. 130 135
Google Scholar
[22] Jiao J, He Y, Kentish S E, Ashokkumar M, Manasseh R, Lee J 2015 Ultrasonics 58 35
Google Scholar
[23] Zilonova E, Solovchuk M, Sheu T W H 2019 Phys. Rev. E 99 023109
Google Scholar
[24] Doinikov A A, Bouakaz A 2014 J. Fluid Mech. 742 425
Google Scholar
[25] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[26] Leighton T G 1994 The Acoustic Bubble (London: Academic Press) p23
-
图 1 管道内双气泡位置示意图(二维)
Figure 1. Schematic diagram of two-bubble positions in the pipeline (two-dimensional).
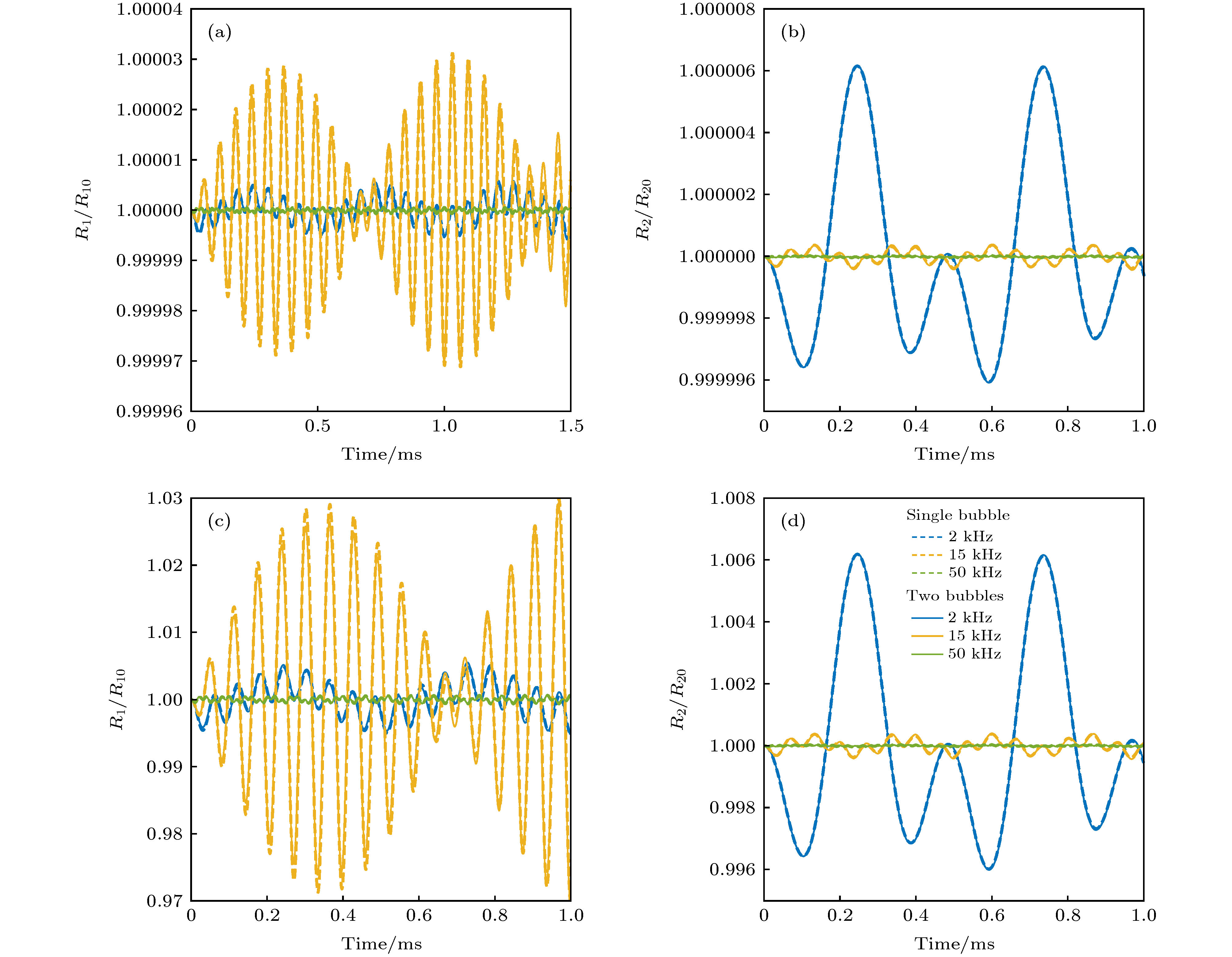
图 2 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的自由气泡与双气泡设置下半径振动特征 (a) 1 Pa声波激励下气泡1在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (b) 1 Pa声波激励下气泡2在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (c) 1 kPa声波激励下气泡1在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (d) 1 kPa声波激励下气泡2在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; 图例在图(d)中给出
Figure 2. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the bubble dynamics under single free and regulated two-bubble vibrations: (a) Relative radius of bubble 1 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 kPa. The figure legend is given in panel (d).
图 3 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的不同气泡距离(2与8 mm)对气泡振动动力学特征影响 (a) 1 Pa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (b) 1 Pa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (c) 1 kPa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (d) 1 kPa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; 图例在图(a)和(c)中给出
Figure 3. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the bubble dynamics under different distances, with 2 mm and 8 mm, between the two bubbles: (a) Relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa. The figure legend is given in panel (a) and (c).
图 4 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的不同气泡距离(2与8 mm)形成的次Bjerknes辐射力 (a) 1 Pa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (b) 1 Pa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (c) 1 kPa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (d) 1 kPa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力
Figure 4. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the second Bjerknes force under different distances, with 2 mm and 8 mm, between the two bubbles: (a) Relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa.
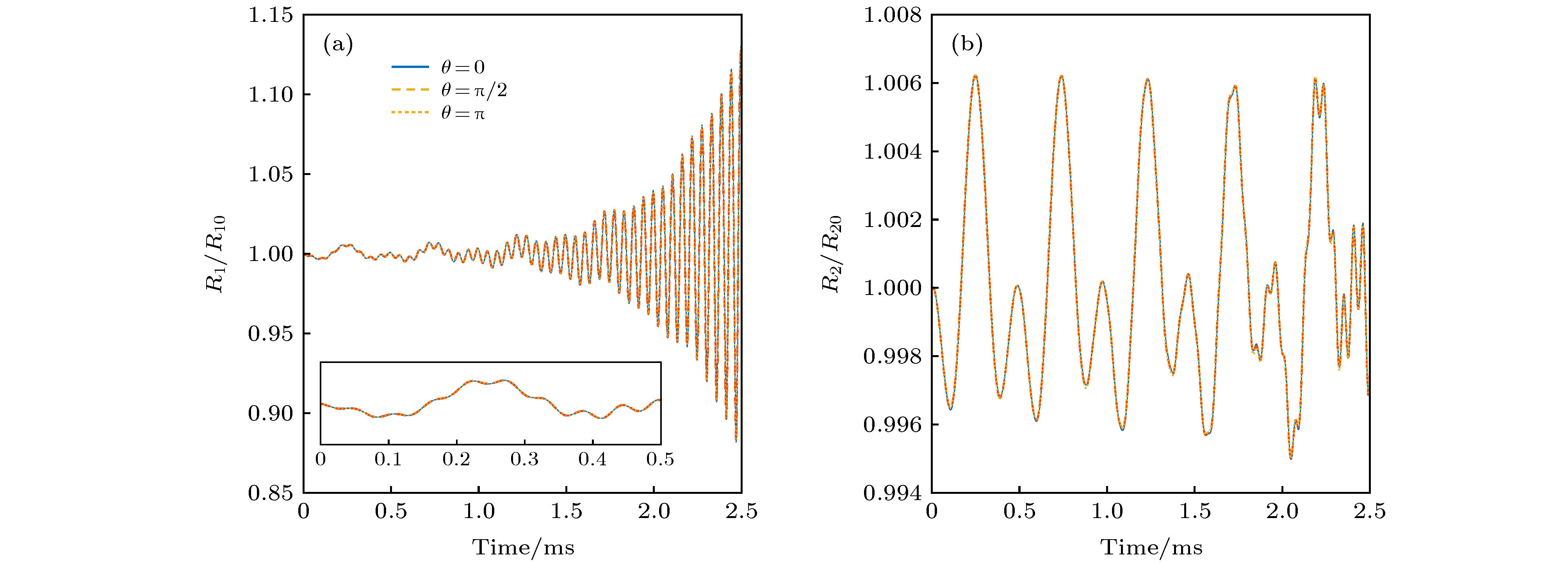
图 5 2 kHz声波激励下不同气泡位置对气泡振动过程的影响 (a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure 5. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 2 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations
图 7 50 kHz声波激励下不同气泡位置对气泡振动过程的影响 (a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure 7. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 50 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations.
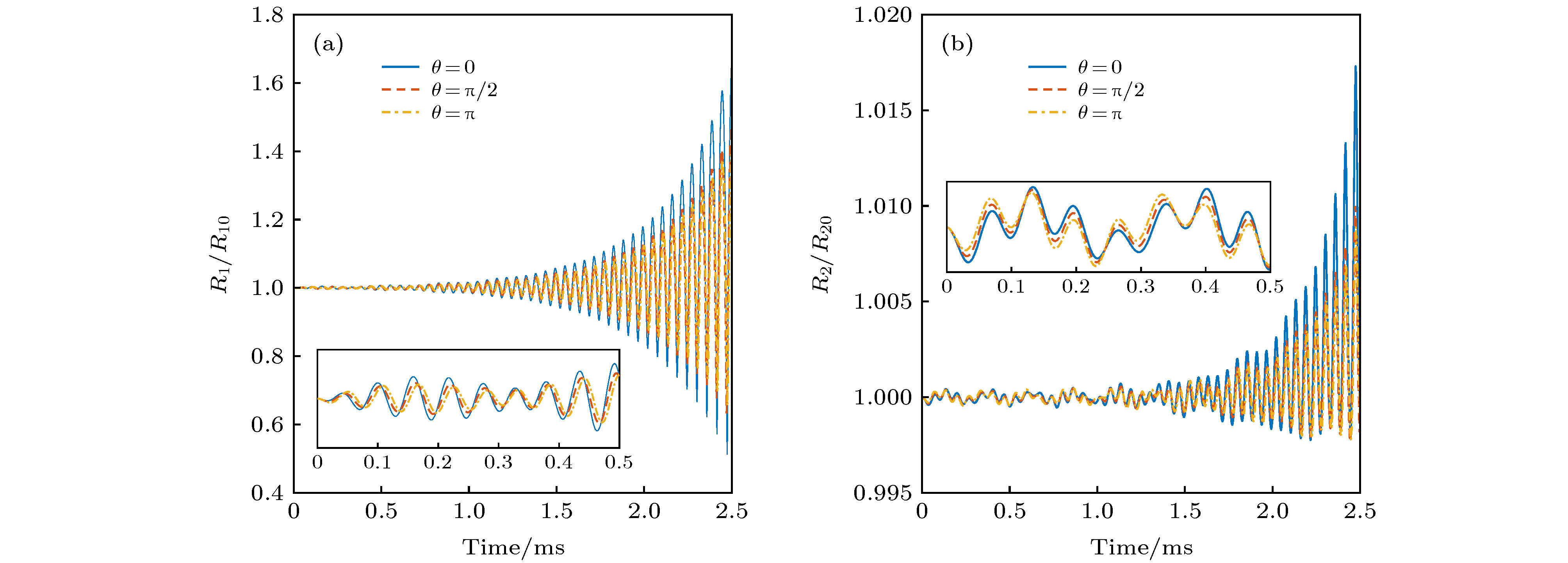
图 6 15 kHz声波激励下不同气泡位置对气泡振动过程的影响 (a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure 6. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 15 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations.
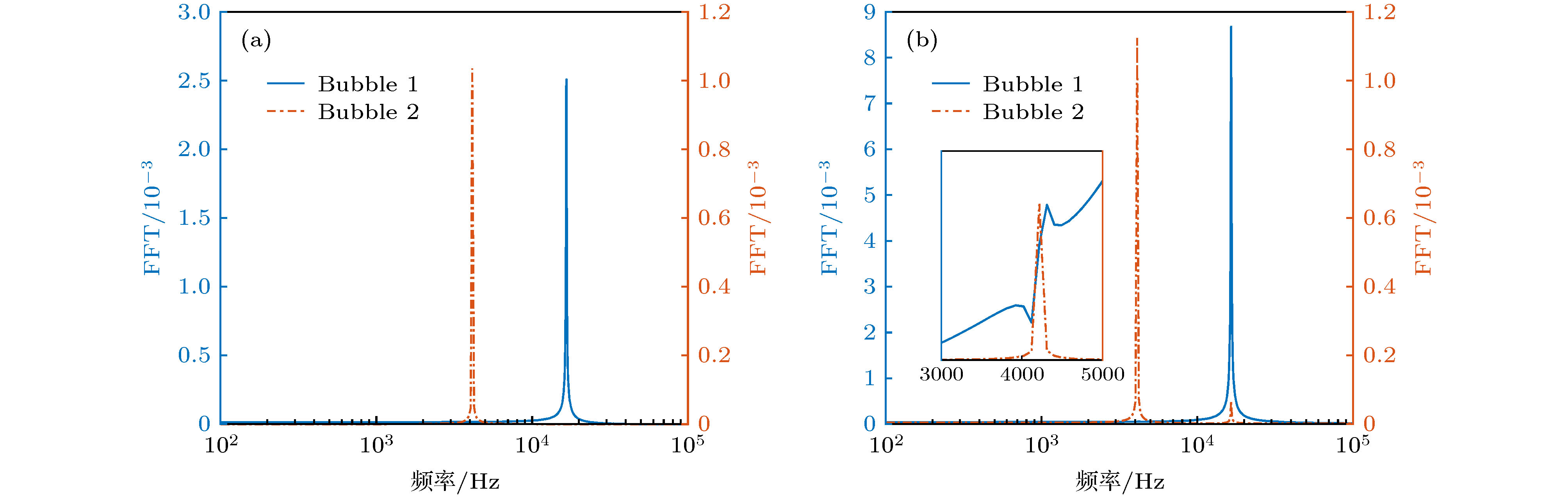
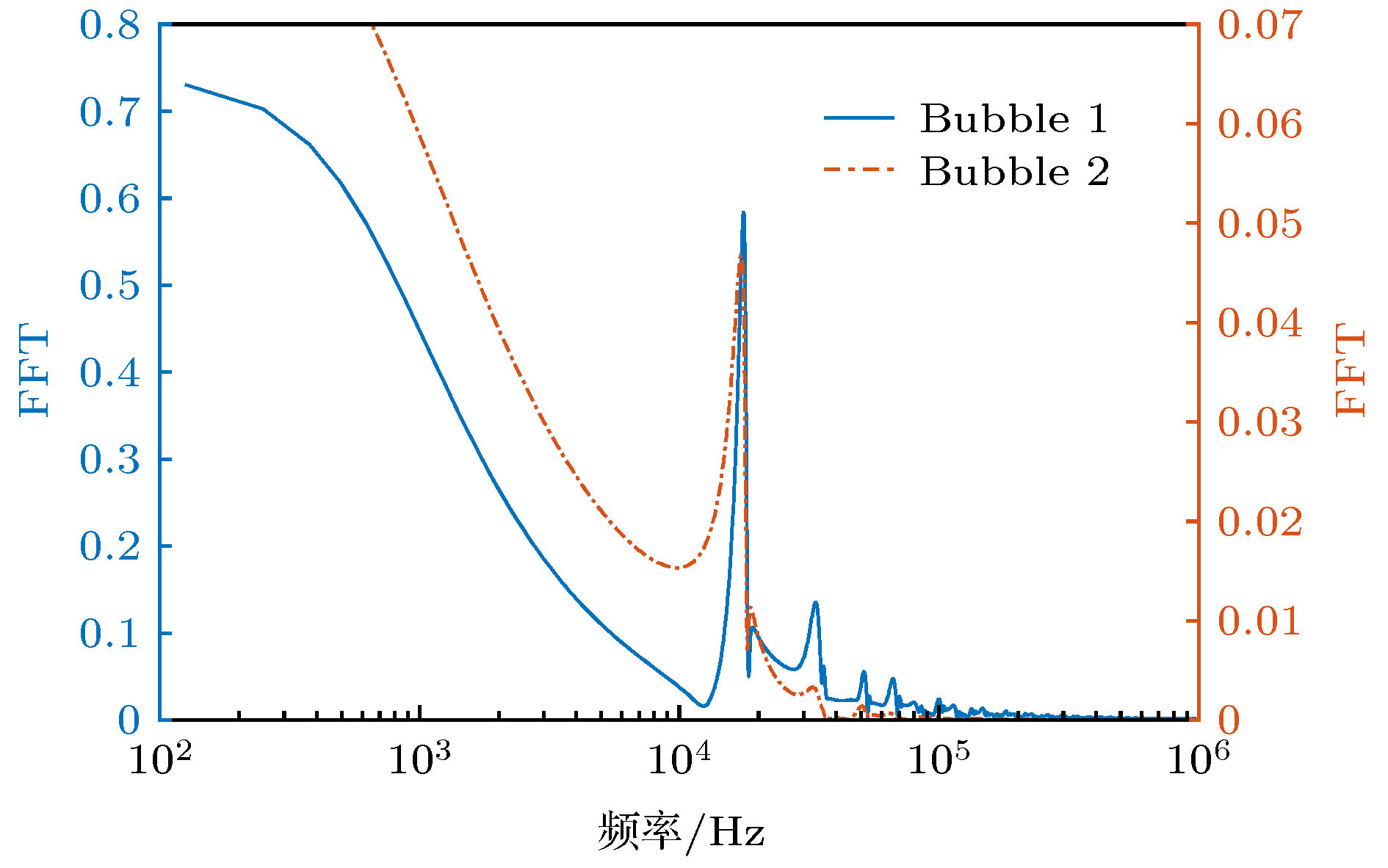
图 8 脉冲激励下气泡幅频响应曲线 (a)自由单气泡对应的幅频响应图; (b)气泡间距离为8 mm下双气泡对应的幅频响应图
Figure 8. Amplitude-frequency response chart of bubble dynamics under pulse excitation: (a) Amplitude-frequency response chart of free single bubble system; (b) amplitude-frequency response chart of two-bubble coupled system with bubble distance being 8 mm.
图 9 双气泡非线性振动对应的频谱响应曲线
Figure 9. Amplitude-frequency response chart of nonlinear two-bubble dynamics under pulse excitation.
-
[1] Balasubramaniam R, Ramé E, Motil B J 2019 Case Western Reserve University Cleveland, Ohio NASA Report No. 20190001795
[2] Wen W, Zong G, Bi S 2014 Rev. Sci. Instrum. 85 065106
Google Scholar
[3] Leighton T G, Ramble D G, Phelps A D 1997 J. Acoust. Soc. Am. 101 2626
Google Scholar
[4] Leighton T G, Baik K, Jiang J 2012 Proc. R. Soc. London, Ser. A 468 2461
Google Scholar
[5] Hsieh D, Plesset M S 1961 Phys. Fluids 4 970
Google Scholar
[6] Sangani A S, Sureshkumar R 1993 J. Fluid Mech. 252 239
Google Scholar
[7] Kerboua K, Hamdaoui O 2019 J. Acoust. Soc. Am. 146 2240
Google Scholar
[8] Ida M, Naoe T, Futakawa M 2007 Phys. Rev. E 75 046304
Google Scholar
[9] Jang N W, Gracewski S I, Abrahamsen B, Buttaccio T, Halm R 2009 J. Acoust. Soc. Am. 126 EL34
Google Scholar
[10] Prosperetti A 1974 J. Acoust. Soc. Am. 56 878
Google Scholar
[11] Feng Z C, Leal L G 1997 Ann. Rev. Fluid Mech. 29 201
Google Scholar
[12] Lauterborn W, Kurz T 2010 Rep. Prog. Phys. 73 106501
Google Scholar
[13] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[14] Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924
Google Scholar
[15] Pelekasis N A, Gaki A, Doinikov A, Tsamopoulos J A 2004 J. Fluid Mech. 500 313
Google Scholar
[16] Liang J, Wang X, Yang J, Gong L 2017 Ultrasonics 75 58
Google Scholar
[17] Omta R 1987 J. Acoust. Soc. Am. 82 1018
Google Scholar
[18] Hamilton M F, Ilinskii Y A, Meegan G D, Zabolotskaya E A 2005 Acoust. Res. Lett. Online 6 207
Google Scholar
[19] Doinikov A A 2004 J. Acoust. Soc. Am. 116 821
Google Scholar
[20] Maiga M A, Coutier-Delgosha O, Buisine D 2018 Phys. Fluids 30 123301
Google Scholar
[21] Yoshida K, Fujikawa T, Watanabe Y 2011 J. Acoust. Soc. Am. 130 135
Google Scholar
[22] Jiao J, He Y, Kentish S E, Ashokkumar M, Manasseh R, Lee J 2015 Ultrasonics 58 35
Google Scholar
[23] Zilonova E, Solovchuk M, Sheu T W H 2019 Phys. Rev. E 99 023109
Google Scholar
[24] Doinikov A A, Bouakaz A 2014 J. Fluid Mech. 742 425
Google Scholar
[25] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[26] Leighton T G 1994 The Acoustic Bubble (London: Academic Press) p23
DownLoad:
Catalog
Metrics
- Abstract views: 6624
- PDF Downloads: 84
- Cited By: 0
