Regulation of entropic uncertainty relation in correlated channels with dephasing colored noise

Yu Min; Guo You-Neng

doi:10.7498/aps.73.20241171

Abstract

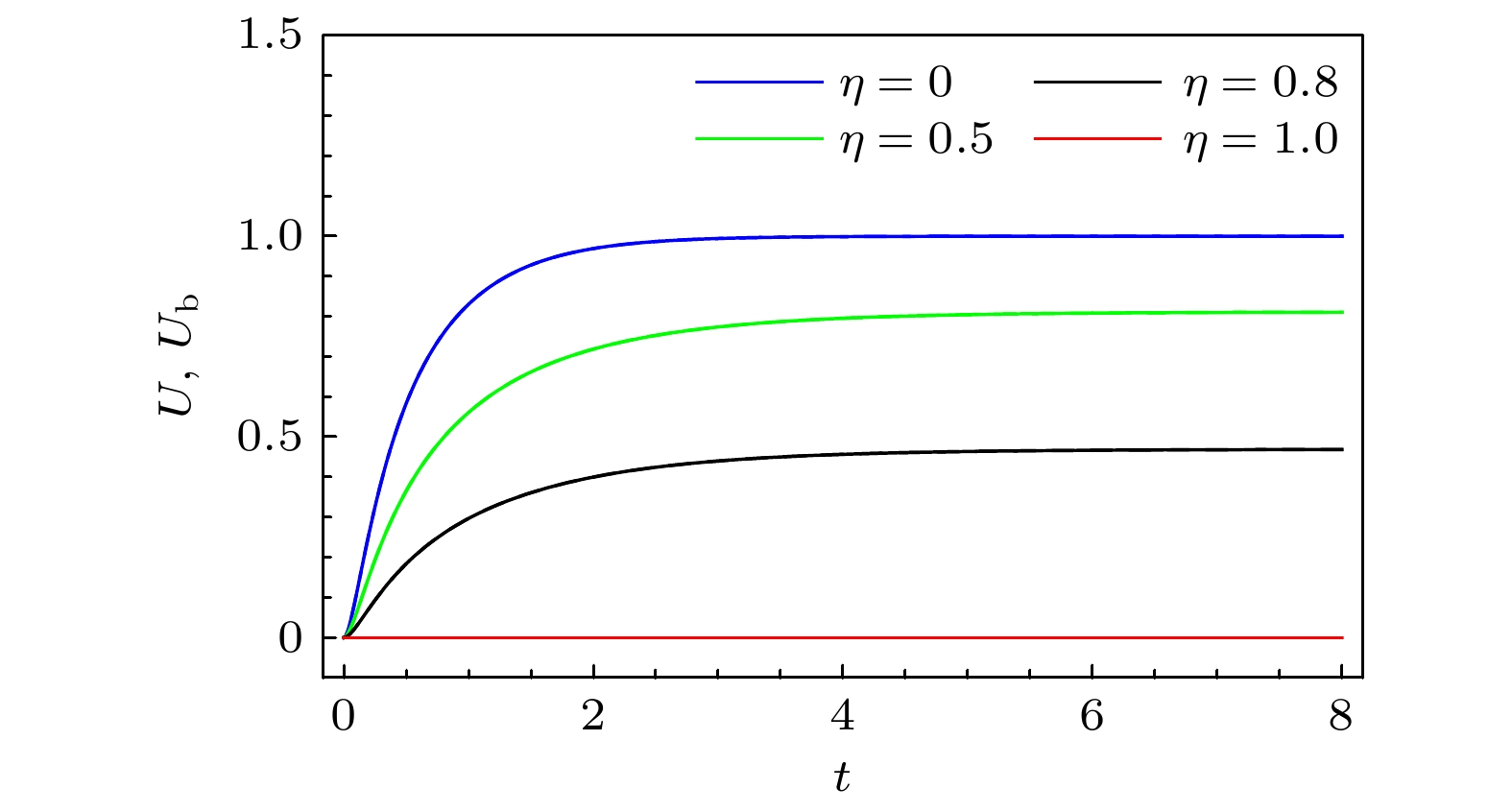
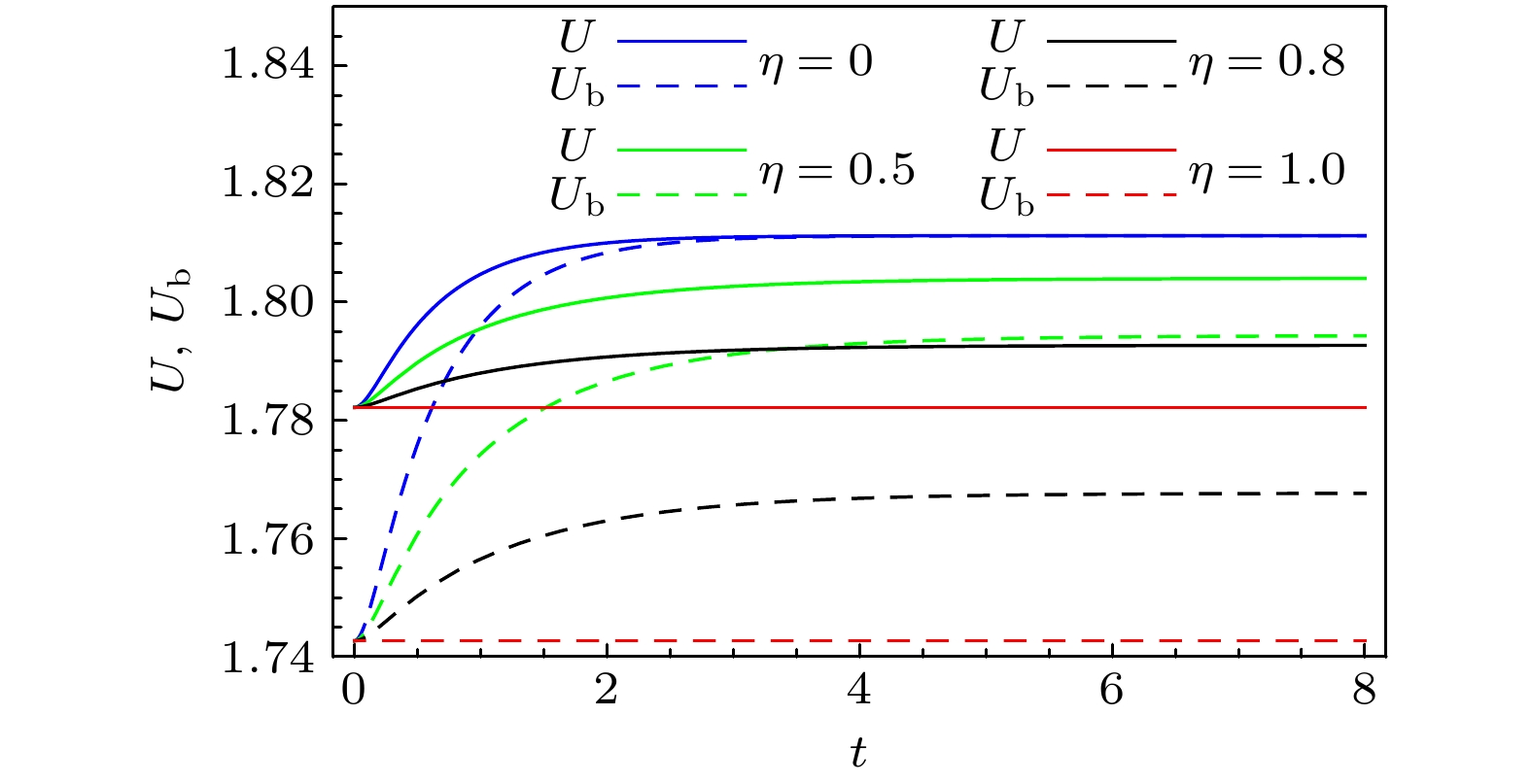
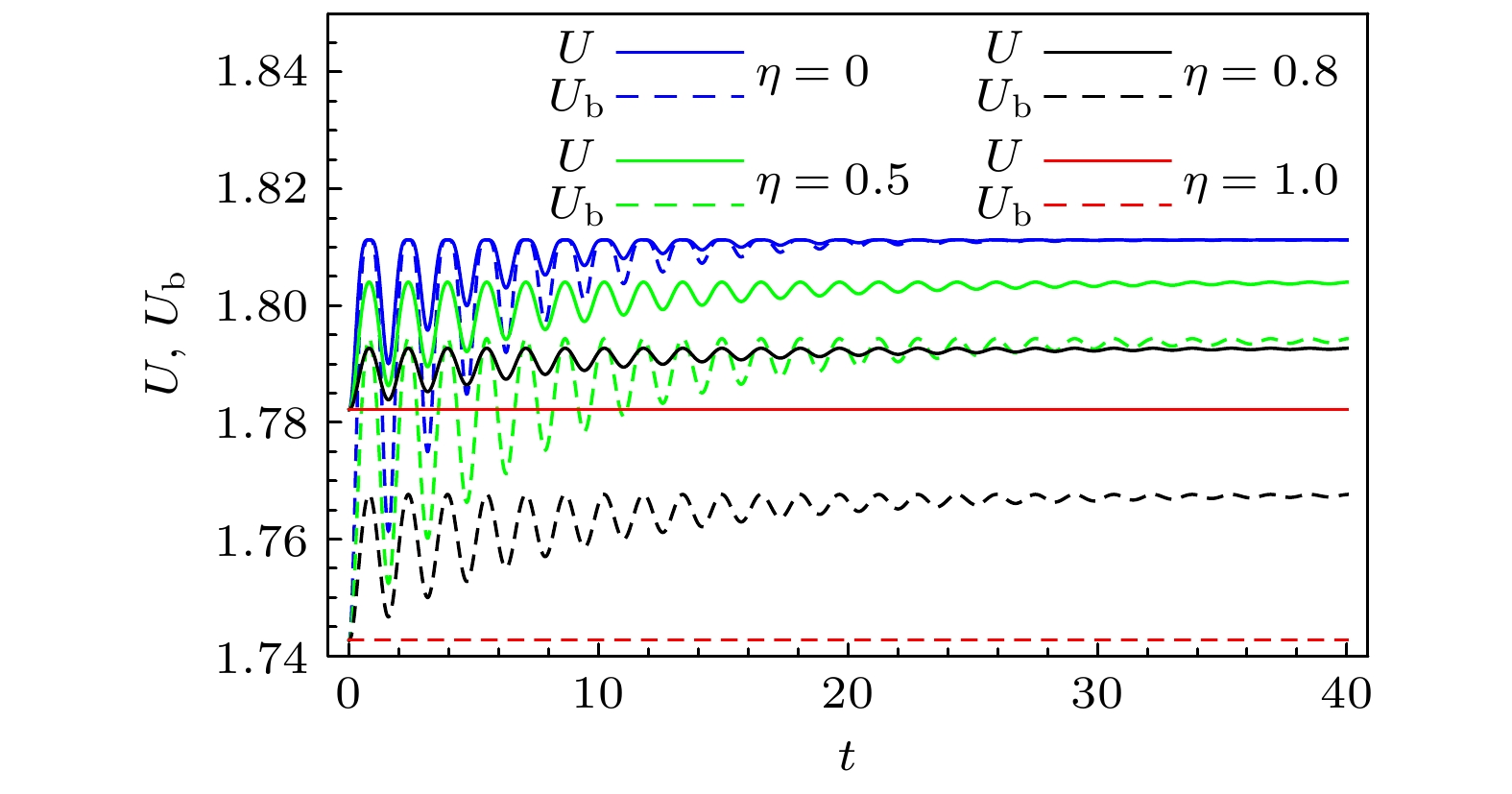
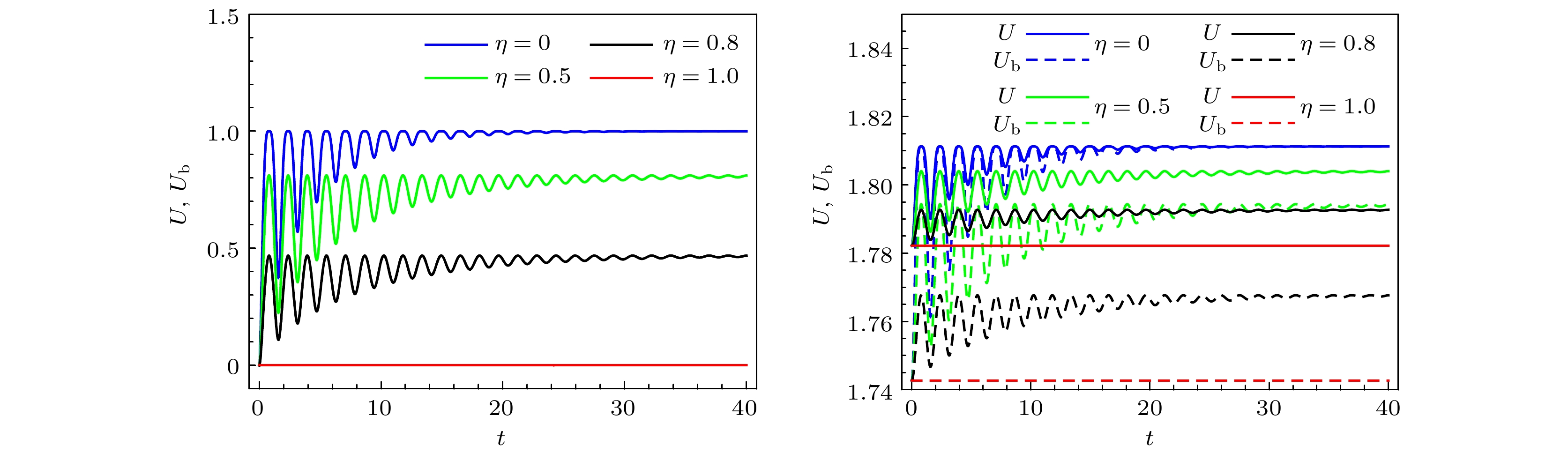
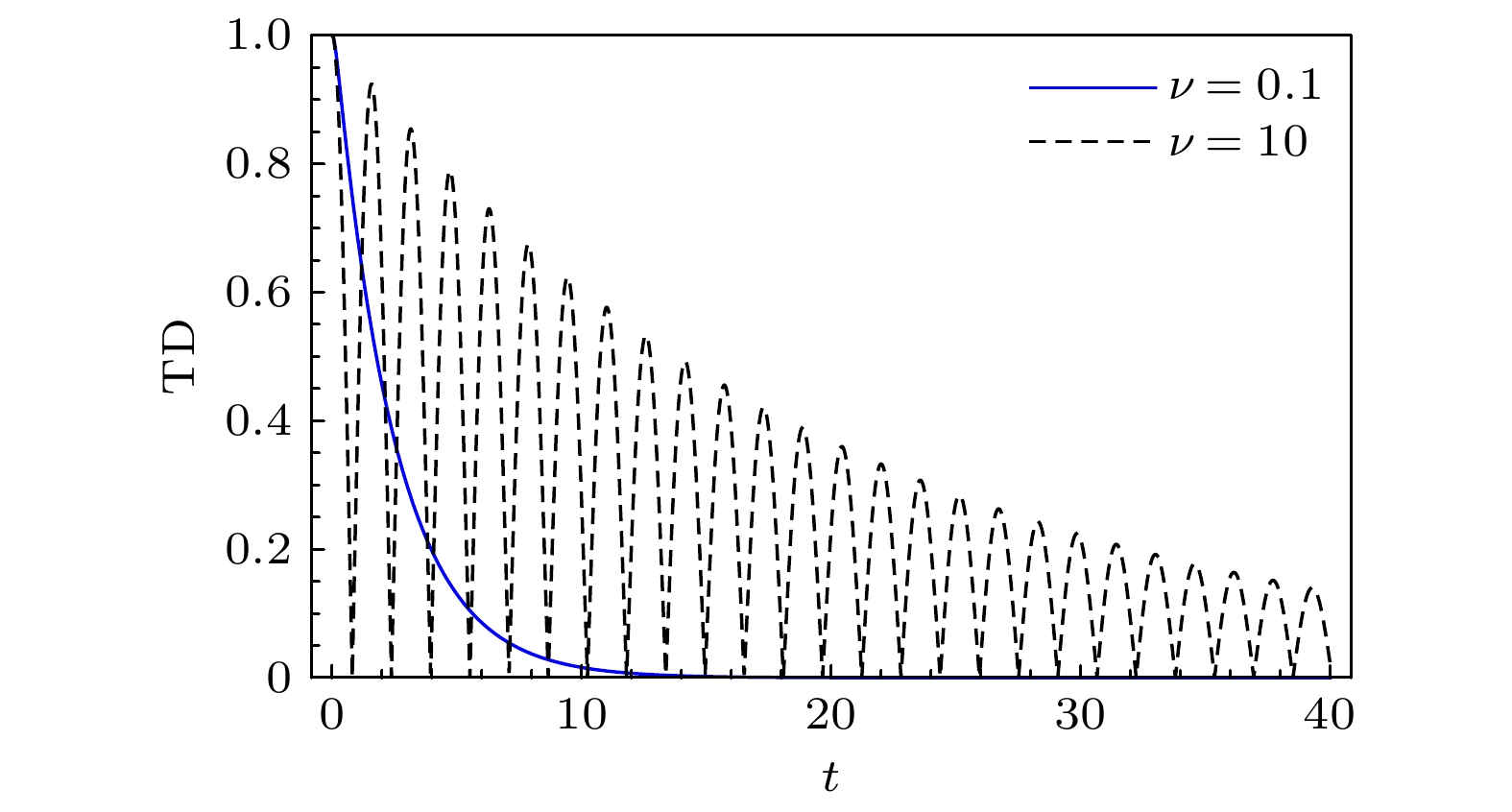
The uncertainty principle limits the ability for observer to precisely measure two incompatible observables, and plays a crucial role in quantum precision measurement in the quantum information science. When quantum systems interact with their surroundings, they inevitably result in decoherence, which increases the uncertainty of the system. In the process of quantum information processing, the effective regulation of uncertainty becomes a key problem that needs to be solved. In this work, we investigate the quantum-memory-assisted entropic uncertainty relation of a two-qubit system under correlated channels with dephasing colored noise. We demonstrate that it is possible to control the entropic uncertainty, U, and its lower bound, U_b, by combining correlations between successive uses of channels and the non-Markovianity of the dynamical evolution. Firstly, the evolutionary characteristics of the trace distance are employed to distinguish between Markovianity and non-Markovianity of the channel. Subsequently, the system is selected to be either a maximally entangled state or separated state initially. By adjusting the strength η of the correlations, we find that with the increase of η, the entropic uncertainty and its lower bound decrease. Especially, if the channel is fully correlated (η = 1), the entropic uncertainty and its lower bound remain constant under the channel, indicating that decoherence is completely suppressed. A comparison of Markovian channel with non-Markovian channel reveals that the entropic uncertainty and its lower bound exhibit oscillatory behaviour under non-Markovian channels. The combination of correlations and non-Markovianity of the channel demonstrates that the entropic uncertainty and its lower bound can be reduced under fully correlated channels where the non-Markovianity has no effect. This is because fully correlated channels suppress decoherence to a greatest extent. Under partially correlated channels, the combination of correlations and non-Markovianity can more effectively reduce the entropic uncertainty and its lower bound. Under such channels, correlations of the channel reduce the entropic uncertainty and its lower bound during the whole evolution, while the non-Markovianity contributes to their oscillations and reduce them in some specific time. Furthermore, the results show that the entropic uncertainty and its lower bound reach steady values that depend only on the strength of the correlations after long-time evolution. In other words, the stronger the correlations, the lower the entropy uncertainty and its lower bound of steady states will be. Finally, we analyse the physical nature of the decrease of the entropic uncertainty and its lower bound, and it is found that the decrease of the entropic uncertainty and its lower bound originate from the increase of the quantum correlations in the system.

Keywords:

Authors and contacts

Yu Min¹,
Guo You-Neng²

1.
Hunan Province Key Laboratory of Photoelectric Information Integration and Optical Manufacturing Technology, College of Mathematics and Physics Science, Hunan University of Arts and Science, Changde 415000, China
2.
School of Electronic Information and Electrical Engineering, Changsha University, Changsha 410022, China

Corresponding author: Yu Min, hsdyumin@163.com

Funds: Project supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2021JJ30757).

FullText HTML : translate this paragraph

References

[1]	Heisenberg W 1927 Z. Phys. 43 172 Google Scholar
[2]	Robertson H P 1929 Phys. Rev. 34 163 Google Scholar
[3]	Deutsch D 1983 Phys. Rev. Lett. 50 631 Google Scholar
[4]	Kraus K 1987 Phys. Rev. D 35 3070 Google Scholar
[5]	Maassen H, Uffink J B M 1988 Phys. Rev. Lett. 60 1103 Google Scholar
[6]	Berta M, Christandl M, Colbeck R, Renes J M, Renner R 2010 Nat. Phys. 6 659 Google Scholar
[7]	Prevedel R, Hamel D R, Colbeck R, Fisher K, Resch K J 2011 Nat. Phys. 7 757 Google Scholar
[8]	Li C F, Xu J S, Xu X Y, Li K, Guo G C 2011 Nat. Phys. 7 752 Google Scholar
[9]	Shi J, Ding Z, Wu T, He J, Yu L, Sun W, Wang D, Ye L 2017 Laser Phys. Lett. 14 125208 Google Scholar
[10]	Hall M J W, Cerf N J 2012 New J. Phys. 14 033040 Google Scholar
[11]	Ekert A K 1991 Phys. Rev. Lett 67 661 Google Scholar
[12]	Renes J M, Boileau J C 2009 Phys. Rev. Lett 103 020402 Google Scholar
[13]	Haseli S, Dolatkhah H, Rangani Jahromi H, Salimi S, Khorashad A S 2020 Opt. Commun. 461 125287 Google Scholar
[14]	Tomamichel M, Lim C C W, Gisin N, Renner R 2012 Nat. Commun. 3 634 Google Scholar
[15]	Ng N H Y, Berta M, Wehner S 2012 Phys. Rev. A 86 042315 Google Scholar
[16]	Ming F, Wang D, Shi W N, Huang A J, Du M M, Sun W Y, Ye L 2018 Quantum Inf. Process. 17 267 Google Scholar
[17]	Li L J, Ming F, Shi W N, Ye L, Wang D 2021 Physica E 133 114802 Google Scholar
[18]	Wang D, Ming F, Huang A J, Sun W Y, Shi J D, Ye L 2017 Laser Phys. Lett. 14 055205 Google Scholar
[19]	Wang D, Ming F, Song X K, Ye L, Chen J L 2020 Eur. Phys. J. C 80 800 Google Scholar
[20]	Li L J, Ming F, Song X K, Ye L, Wang D 2021 Eur. Phys. J. C 81 72 Google Scholar
[21]	Wang T Y, Wang D 2024 Phys. Lett. B 855 138876 Google Scholar
[22]	Wang T Y, Wang D 2024 Phys. Lett. A 499 129364 Google Scholar
[23]	Wu L, Ye L, Wang D 2022 Phys. Rev. A 106 062219 Google Scholar
[24]	Xie B F, Ming F, Wang D, Ye L, Chen J L 2021 Phys. Rev. A 104 062204 Google Scholar
[25]	Ming F, Wang D, Fan X G, Shi W N, Ye L, Chen J L 2020 Phys. Rev. A 102 012206 Google Scholar
[26]	Bouafia Z, Oumennana M, Mansour M, Ouchni F 2024 Appl. Phys. B 130 94 Google Scholar
[27]	Abdel-Wahab N H, Ibrahim T A S, Amin M E, Salah A 2024 Eur. Phys. J. D 78 28 Google Scholar
[28]	Macchiavello C, Palma G M 2002 Phys. Rev. A 65 050301 Google Scholar
[29]	D’Arrigo A, Benenti G, Falci G 2007 New. J. Phys. 9 310 Google Scholar
[30]	D’Arrigo A, Benenti G, Falci G 2013 Phys. Rev. A 88 042337 Google Scholar
[31]	Sk R, Panigrehi P K 2024 Phys. Rev. A 109 032425 Google Scholar
[32]	Guo Y N, Fang M F, Wang G Y, Zeng K 2016 Quantum Inf. Process. 15 5129 Google Scholar
[33]	Peng Z Y, Wu F L, Li J, Xue H N, Liu S Y, Wang Z Y 2023 Phys. Rev. A 107 022405 Google Scholar
[34]	Yu M, Guo Y N 2024 Int. J. Theor. Phys. 63 156 Google Scholar
[35]	Xie Y X, Qin Z Y 2020 Quantum Inf. Process. 19 375 Google Scholar
[36]	董曜, 纪爱玲, 张国锋 2022 物理学报 71 070303 Google Scholar Dong Y, Ji A L, Zhang G F 2022 Acta Phys. Sin. 71 070303 Google Scholar
[37]	Zhang D H, Wu F L, Peng Z Y, Wang L, Liu S Y 2023 Quantum Inf. Process. 22 120 Google Scholar
[38]	Xu K, Zhang G F, Liu W M 2019 Phys. Rev. A 100 052305 Google Scholar
[39]	Haseli S, Hadipour M 2022 Int. J. Theor. Phys. 61 117 Google Scholar
[40]	Awasthi N, Joshi D K, Sachdev S 2022 Int. J. Theor. Phys. 61 123 Google Scholar
[41]	Hou L, Zhang Y , Zhu Y 2023 Int. J. Theor. Phys. 62 221 Google Scholar
[42]	Lindblad G 1976 Comm. Math. Phys. 48 119 Google Scholar
[43]	Wolf M M, Eisert J, Cubitt T S, Cirac J I 2008 Phys. Rev. Lett. 101 150402 Google Scholar
[44]	Lambert N, Chen Y N, Cheng Y C, Li C M, Chen G Y, Nori F 2013 Nat. Phys. 9 10 Google Scholar
[45]	Hwang B, Goan H S 2012 Phys. Rev. A 85 032321 Google Scholar
[46]	Banu H, Rao K R 2024 Eur. Phys. J. Plus 139 436 Google Scholar
[47]	Addis C, Karpat G, Macchiavello C, Maniscalco 2016 Phys. Rev. A 94 032121 Google Scholar
[48]	Awasthi N, Haseli S, Johri U C, Salimi S, Dolatkhah H 2020 Quantum Inf. Process. 19 10 Google Scholar
[49]	Wang G Y, Guo Y N, Zeng K 2019 J. Mod. Opt. 66 367 Google Scholar
[50]	李丽娟, 明飞, 宋学科, 叶柳, 王栋 2022 物理学报 71 070302 Google Scholar Li L J, Ming F, Song X K, Ye L, Wang D 2022 Acta Phys. Sin. 71 070302 Google Scholar
[51]	Hajihoseinlou H, Ahansaz B 2024 Laser Phys. 34 075202 Google Scholar
[52]	Daffer S, Wodkiewicz K, Cresser J D, McIver J K 2004 Phys. Rev. A 70 010304(R Google Scholar
[53]	Cai X 2020 Sci. Rep. 10 88 Google Scholar
[54]	Breuer H P, Laine E M, Piilo J 2009 Phys. Rev. Lett. 103 210401 Google Scholar
[55]	Chen M N, Wang D, Ye L 2019 Phys. Lett. A 383 977 Google Scholar
[56]	Wang D, Huang A J, Hoehn R D, Ming F, Sun W Y, Shi J Dong, Ye L, Kais S 2017 Sci. Rep. 7 1066 Google Scholar
[57]	Xu Z Y, Yang W L, Feng M 2012 Phys. Rev. A 86 012113 Google Scholar
[58]	Hu M L, Zhou W 2019 Laser Phys. Lett. 16 045201 Google Scholar
[59]	Hu M L, Fan H 2020 Sci. China-Phys. Mech. Astron. 63 230322 Google Scholar
[60]	Hu M L, Zhang Y H, Fan H 2021 Chin. Phys. B 30 030308 Google Scholar
[61]	Wootters W K 1998 Phys. Rev. Lett. 80 2245 Google Scholar
[62]	Ollivier H, Zurek W H 2001 Phys. Rev. Lett. 88 017901 Google Scholar
[63]	Mazzola L, Piilo J, Maniscalco S 2011 Int. J. Quantum Inf. 09 981 Google Scholar
[64]	Pati A K, Wilde M M, Devi A R U, Rajagopal A K, Sudha 2012 Phys. Rev. A 86 042105 Google Scholar
[65]	Hu M L, Fan H 2013 Phys. Rev. A 88 014105 Google Scholar
[66]	Hu M L, Fan H 2013 Phys. Rev. A 87 022314 Google Scholar

Cited By

图 1 迹距离TD随时间的演化

Figure 1. Evolution of the trace distance TD.

DownLoad: Full-Size Img PowerPoint

图 2 初态为最大纠缠态时, 熵不确定度U及其下限$ U_{{\mathrm{b}}} $随时间的演化. 通道参数$ \nu=0.1 $, 呈现马尔科夫性

Figure 2. Evolution of uncertainty U and its lower bound $ U_{{\mathrm{b}}} $ of the system which is initially in a maximally entangled state. The channel is Markovian, where $ \nu=0.1 $.

DownLoad: Full-Size Img PowerPoint

图 3 初态为最大纠缠态时, 熵不确定度U及其下限$ U_{{\mathrm{b}}} $随时间的演化. 通道参数$ \nu=10 $, 呈现非马尔科夫性

Figure 3. Evolution of uncertainty U and its lower bound $ U_{{\mathrm{b}}} $ of the system which is initially in a maximally entangled state. The channel is non-Markovian, where $ \nu=10 $

DownLoad: Full-Size Img PowerPoint

图 4 初态为可分离态时熵不确定度U及其下限$ U_{{\mathrm{b}}} $随时间的演化. 通道参数$ \nu=0.1 $, 呈现马尔科夫性

Figure 4. Evolution of uncertainty U and its lower bound $ U_{{\mathrm{b}}} $ of the system which is initially in a separated state. The channel is Markovian, where $ \nu=0.1 $.

DownLoad: Full-Size Img PowerPoint

图 5 初态为可分离态时, 熵不确定度U及其下限$ U_{{\mathrm{b}}} $随时间的演化. 通道参数$ \nu=10 $, 呈现非马尔科夫性

Figure 5. Evolution of uncertainty U and its lower bound $ U_{{\mathrm{b}}} $ of the system which is initially in a separated state. The channel is non-Markovian, where $ \nu=10 $.

DownLoad: Full-Size Img PowerPoint

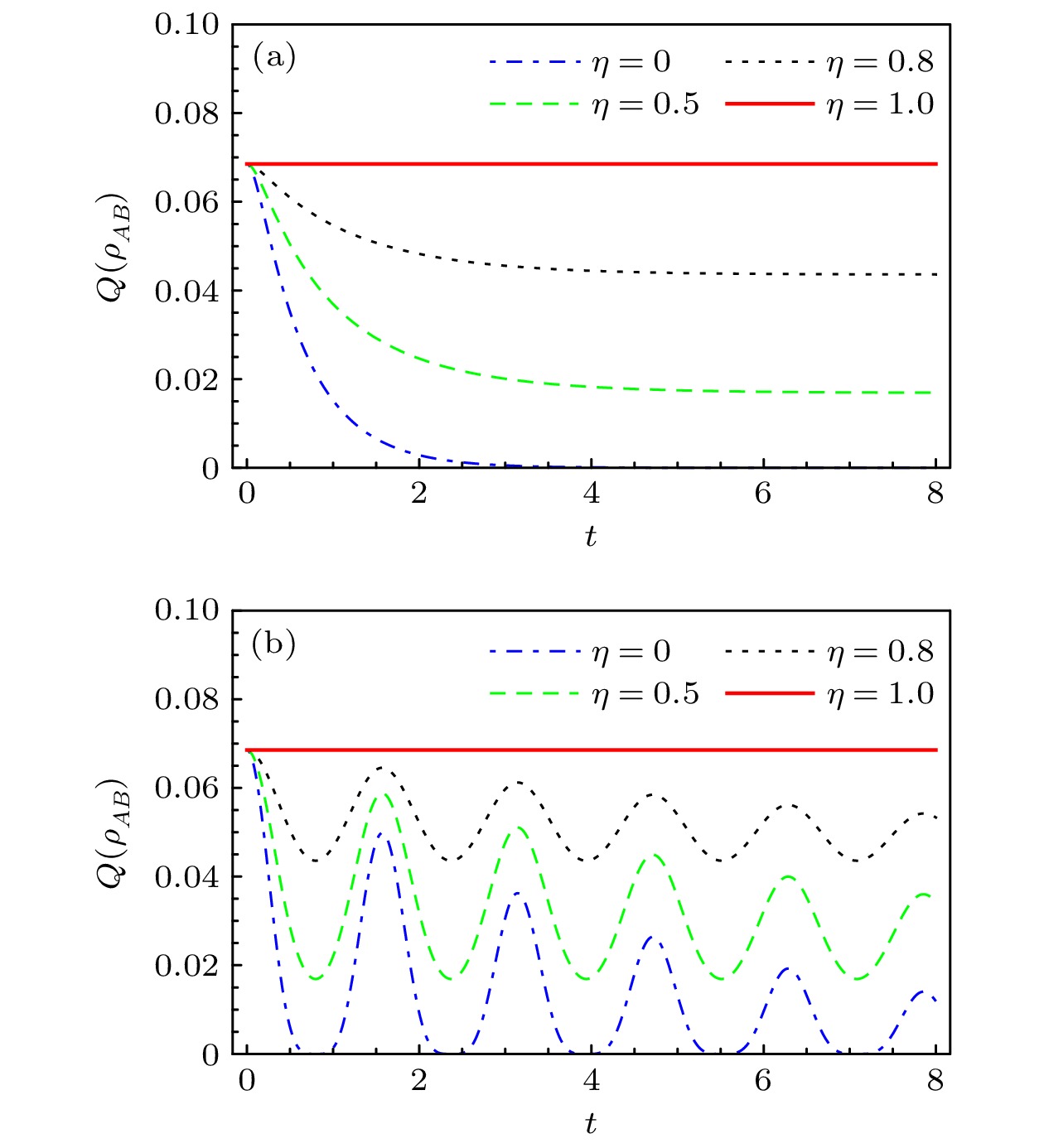
图 6 初态为可分离态时量子关联$ Q({\boldsymbol{\rho}}_{AB}) $随时间的演化(a)通道参数$ \nu= 0.1 $, 呈现马尔科夫性; (b)通道参数$ \nu=10 $, 呈现非马尔科夫性

Figure 6. Evolution of quantum correlations $ Q({\boldsymbol{\rho}}_{AB}) $ of the system which is initially in a separated state: (a) The channel is Markovian, where $ \nu=0.1 $; (b) the channel is non-Markovian, where $ \nu=10 $.

DownLoad: Full-Size Img PowerPoint

DownLoad: Full-Size Img PowerPoint

[1]	Heisenberg W 1927 Z. Phys. 43 172 Google Scholar
[2]	Robertson H P 1929 Phys. Rev. 34 163 Google Scholar
[3]	Deutsch D 1983 Phys. Rev. Lett. 50 631 Google Scholar
[4]	Kraus K 1987 Phys. Rev. D 35 3070 Google Scholar
[5]	Maassen H, Uffink J B M 1988 Phys. Rev. Lett. 60 1103 Google Scholar
[6]	Berta M, Christandl M, Colbeck R, Renes J M, Renner R 2010 Nat. Phys. 6 659 Google Scholar
[7]	Prevedel R, Hamel D R, Colbeck R, Fisher K, Resch K J 2011 Nat. Phys. 7 757 Google Scholar
[8]	Li C F, Xu J S, Xu X Y, Li K, Guo G C 2011 Nat. Phys. 7 752 Google Scholar
[9]	Shi J, Ding Z, Wu T, He J, Yu L, Sun W, Wang D, Ye L 2017 Laser Phys. Lett. 14 125208 Google Scholar
[10]	Hall M J W, Cerf N J 2012 New J. Phys. 14 033040 Google Scholar
[11]	Ekert A K 1991 Phys. Rev. Lett 67 661 Google Scholar
[12]	Renes J M, Boileau J C 2009 Phys. Rev. Lett 103 020402 Google Scholar
[13]	Haseli S, Dolatkhah H, Rangani Jahromi H, Salimi S, Khorashad A S 2020 Opt. Commun. 461 125287 Google Scholar
[14]	Tomamichel M, Lim C C W, Gisin N, Renner R 2012 Nat. Commun. 3 634 Google Scholar
[15]	Ng N H Y, Berta M, Wehner S 2012 Phys. Rev. A 86 042315 Google Scholar
[16]	Ming F, Wang D, Shi W N, Huang A J, Du M M, Sun W Y, Ye L 2018 Quantum Inf. Process. 17 267 Google Scholar
[17]	Li L J, Ming F, Shi W N, Ye L, Wang D 2021 Physica E 133 114802 Google Scholar
[18]	Wang D, Ming F, Huang A J, Sun W Y, Shi J D, Ye L 2017 Laser Phys. Lett. 14 055205 Google Scholar
[19]	Wang D, Ming F, Song X K, Ye L, Chen J L 2020 Eur. Phys. J. C 80 800 Google Scholar
[20]	Li L J, Ming F, Song X K, Ye L, Wang D 2021 Eur. Phys. J. C 81 72 Google Scholar
[21]	Wang T Y, Wang D 2024 Phys. Lett. B 855 138876 Google Scholar
[22]	Wang T Y, Wang D 2024 Phys. Lett. A 499 129364 Google Scholar
[23]	Wu L, Ye L, Wang D 2022 Phys. Rev. A 106 062219 Google Scholar
[24]	Xie B F, Ming F, Wang D, Ye L, Chen J L 2021 Phys. Rev. A 104 062204 Google Scholar
[25]	Ming F, Wang D, Fan X G, Shi W N, Ye L, Chen J L 2020 Phys. Rev. A 102 012206 Google Scholar
[26]	Bouafia Z, Oumennana M, Mansour M, Ouchni F 2024 Appl. Phys. B 130 94 Google Scholar
[27]	Abdel-Wahab N H, Ibrahim T A S, Amin M E, Salah A 2024 Eur. Phys. J. D 78 28 Google Scholar
[28]	Macchiavello C, Palma G M 2002 Phys. Rev. A 65 050301 Google Scholar
[29]	D’Arrigo A, Benenti G, Falci G 2007 New. J. Phys. 9 310 Google Scholar
[30]	D’Arrigo A, Benenti G, Falci G 2013 Phys. Rev. A 88 042337 Google Scholar
[31]	Sk R, Panigrehi P K 2024 Phys. Rev. A 109 032425 Google Scholar
[32]	Guo Y N, Fang M F, Wang G Y, Zeng K 2016 Quantum Inf. Process. 15 5129 Google Scholar
[33]	Peng Z Y, Wu F L, Li J, Xue H N, Liu S Y, Wang Z Y 2023 Phys. Rev. A 107 022405 Google Scholar
[34]	Yu M, Guo Y N 2024 Int. J. Theor. Phys. 63 156 Google Scholar
[35]	Xie Y X, Qin Z Y 2020 Quantum Inf. Process. 19 375 Google Scholar
[36]	董曜, 纪爱玲, 张国锋 2022 物理学报 71 070303 Google Scholar Dong Y, Ji A L, Zhang G F 2022 Acta Phys. Sin. 71 070303 Google Scholar
[37]	Zhang D H, Wu F L, Peng Z Y, Wang L, Liu S Y 2023 Quantum Inf. Process. 22 120 Google Scholar
[38]	Xu K, Zhang G F, Liu W M 2019 Phys. Rev. A 100 052305 Google Scholar
[39]	Haseli S, Hadipour M 2022 Int. J. Theor. Phys. 61 117 Google Scholar
[40]	Awasthi N, Joshi D K, Sachdev S 2022 Int. J. Theor. Phys. 61 123 Google Scholar
[41]	Hou L, Zhang Y , Zhu Y 2023 Int. J. Theor. Phys. 62 221 Google Scholar
[42]	Lindblad G 1976 Comm. Math. Phys. 48 119 Google Scholar
[43]	Wolf M M, Eisert J, Cubitt T S, Cirac J I 2008 Phys. Rev. Lett. 101 150402 Google Scholar
[44]	Lambert N, Chen Y N, Cheng Y C, Li C M, Chen G Y, Nori F 2013 Nat. Phys. 9 10 Google Scholar
[45]	Hwang B, Goan H S 2012 Phys. Rev. A 85 032321 Google Scholar
[46]	Banu H, Rao K R 2024 Eur. Phys. J. Plus 139 436 Google Scholar
[47]	Addis C, Karpat G, Macchiavello C, Maniscalco 2016 Phys. Rev. A 94 032121 Google Scholar
[48]	Awasthi N, Haseli S, Johri U C, Salimi S, Dolatkhah H 2020 Quantum Inf. Process. 19 10 Google Scholar
[49]	Wang G Y, Guo Y N, Zeng K 2019 J. Mod. Opt. 66 367 Google Scholar
[50]	李丽娟, 明飞, 宋学科, 叶柳, 王栋 2022 物理学报 71 070302 Google Scholar Li L J, Ming F, Song X K, Ye L, Wang D 2022 Acta Phys. Sin. 71 070302 Google Scholar
[51]	Hajihoseinlou H, Ahansaz B 2024 Laser Phys. 34 075202 Google Scholar
[52]	Daffer S, Wodkiewicz K, Cresser J D, McIver J K 2004 Phys. Rev. A 70 010304(R Google Scholar
[53]	Cai X 2020 Sci. Rep. 10 88 Google Scholar
[54]	Breuer H P, Laine E M, Piilo J 2009 Phys. Rev. Lett. 103 210401 Google Scholar
[55]	Chen M N, Wang D, Ye L 2019 Phys. Lett. A 383 977 Google Scholar
[56]	Wang D, Huang A J, Hoehn R D, Ming F, Sun W Y, Shi J Dong, Ye L, Kais S 2017 Sci. Rep. 7 1066 Google Scholar
[57]	Xu Z Y, Yang W L, Feng M 2012 Phys. Rev. A 86 012113 Google Scholar
[58]	Hu M L, Zhou W 2019 Laser Phys. Lett. 16 045201 Google Scholar
[59]	Hu M L, Fan H 2020 Sci. China-Phys. Mech. Astron. 63 230322 Google Scholar
[60]	Hu M L, Zhang Y H, Fan H 2021 Chin. Phys. B 30 030308 Google Scholar
[61]	Wootters W K 1998 Phys. Rev. Lett. 80 2245 Google Scholar
[62]	Ollivier H, Zurek W H 2001 Phys. Rev. Lett. 88 017901 Google Scholar
[63]	Mazzola L, Piilo J, Maniscalco S 2011 Int. J. Quantum Inf. 09 981 Google Scholar
[64]	Pati A K, Wilde M M, Devi A R U, Rajagopal A K, Sudha 2012 Phys. Rev. A 86 042105 Google Scholar
[65]	Hu M L, Fan H 2013 Phys. Rev. A 88 014105 Google Scholar
[66]	Hu M L, Fan H 2013 Phys. Rev. A 87 022314 Google Scholar

[1]	Jiang Shi-Min, Jia Xin-Yan, Fan Dai-He. Quantum non-local correlation testing of Werner state in non-Markovian environment. Acta Physica Sinica, 2024, 73(16): 160301. doi: 10.7498/aps.73.20240450
[2]	Hu Fei-Fei, Li Si-Ying, Zhu Shun, Huang Yu, Lin Xu-Bin, Zhang Si-Tuo, Fan Yun-Ru, Zhou Qiang, Liu Yun. Generation of multiwavelength quantum correlated photon pair for quantum entanglement key distribution. Acta Physica Sinica, 2024, 73(23): 230304. doi: 10.7498/aps.73.20241274
[3]	Zeng Bai-Yun, Gu Peng-Yu, Jiang Shi-Min, Jia Xin-Yan, Fan Dai-He. Quantum nonlocality testing of the “X” state based on the CHSH inequality in Markov environment. Acta Physica Sinica, 2023, 72(5): 050301. doi: 10.7498/aps.72.20222218
[4]	Zhang Shi-Qi, Yang Hua-Tong. Quantitative description of uncertainty andentropic uncertainty relation. Acta Physica Sinica, 2023, 72(11): 110303. doi: 10.7498/aps.72.20222443
[5]	Hu Qiang, Zeng Bai-Yun, Gu Peng-Yu, Jia Xin-Yan, Fan Dai-He. Testing quantum nonlocality of two-qubit entangled states under decoherence. Acta Physica Sinica, 2022, 71(7): 070301. doi: 10.7498/aps.71.20211453
[6]	Zeng Bai-Yun, Gu Peng-Yu, Hu Qiang, Jia Xin-Yan, Fan Dai-He. Quantum nonlocal test of “X” state based on geometric interpretation of CHSH inequality. Acta Physica Sinica, 2022, 71(17): 170302. doi: 10.7498/aps.71.20220445
[7]	He Zhi, Jiang Deng-Kui, Li Yan. Non-Markovian measure independent of initial states of open systems. Acta Physica Sinica, 2022, 71(21): 210303. doi: 10.7498/aps.71.20221053
[8]	Li Li-Juan, Ming Fei, Song Xue-Ke, Ye Liu, Wang Dong. Review on entropic uncertainty relations. Acta Physica Sinica, 2022, 71(7): 070302. doi: 10.7498/aps.71.20212197
[9]	Zhang Jin-Feng, Arapat Ablimit, Yang Fan, Akbar Hamutjan, Tang Shi-Sheng, Ahmad Abliz. Effects of Kaplan-Shekhtman-Entin-Wohlman-Aharony interaction on quantum discord of non-markovian dynamics under different magnetic fields. Acta Physica Sinica, 2021, 70(22): 223401. doi: 10.7498/aps.70.20211277
[10]	Zhang Shi-Hao, Zhang Xiang-Dong, Li Lü-Zhou. Research progress of measurement-based quantum computation. Acta Physica Sinica, 2021, 70(21): 210301. doi: 10.7498/aps.70.20210923
[11]	Yang Yang, Wang An-Min, Cao Lian-Zhen, Zhao Jia-Qiang, Lu Huai-Xin. Correlation and coherence for two-qubit system coupled to XY spin chains. Acta Physica Sinica, 2018, 67(15): 150302. doi: 10.7498/aps.67.20180812
[12]	You Bo, Cen Li-Xiang. Phenomena of limit cycle oscillations for non-Markovian dissipative systems undergoing long-time evolution. Acta Physica Sinica, 2015, 64(21): 210302. doi: 10.7498/aps.64.210302
[13]	Qin Meng, Li Yan-Biao, Bai Zhong. Effects of inhomogeneous magnetic field and magnetic impurity on the quantum correlation of spin-1 system. Acta Physica Sinica, 2015, 64(3): 030301. doi: 10.7498/aps.64.030301
[14]	Li Jing, Zhao Yong-Jun, Li Dong-Hai. Time delay estimation using Markov Chain Monte Carlo method. Acta Physica Sinica, 2014, 63(13): 130701. doi: 10.7498/aps.63.130701
[15]	Xie Mei-Qiu, Guo Bin. Thermal quantum discord in Heisenberg XXZ model under different magnetic field conditions. Acta Physica Sinica, 2013, 62(11): 110303. doi: 10.7498/aps.62.110303
[16]	Fan Kai-Ming, Zhang Guo-Feng. The dynamics of quantum correlation between two atoms in a damping Jaynes-Cummings model. Acta Physica Sinica, 2013, 62(13): 130301. doi: 10.7498/aps.62.130301
[17]	Yang Yang, Wang An-Min. Quantum correlation for a central two-qubit system coupled to Ising chain. Acta Physica Sinica, 2013, 62(13): 130305. doi: 10.7498/aps.62.130305
[18]	Hou Zhou-Guo, He Yi-Gang, Li Bing. Radio frequency identification anti-collision test based on Markov chain model. Acta Physica Sinica, 2011, 60(2): 025211. doi: 10.7498/aps.60.025211
[19]	WANG HONG-WEI. ELECTRON CORRELATION IN QUANTUM WELLS. Acta Physica Sinica, 1997, 46(8): 1618-1624. doi: 10.7498/aps.46.1618
[20]	HUANG XIANG-YOU. THE CLASSICAL ANALOGY OF UNCERTAINTY RELATION. Acta Physica Sinica, 1996, 45(3): 353-359. doi: 10.7498/aps.45.353

Catalog

Vol. 73, Issue 22 - 2024-11-20

Metrics

Abstract views: 760
PDF Downloads: 44
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板