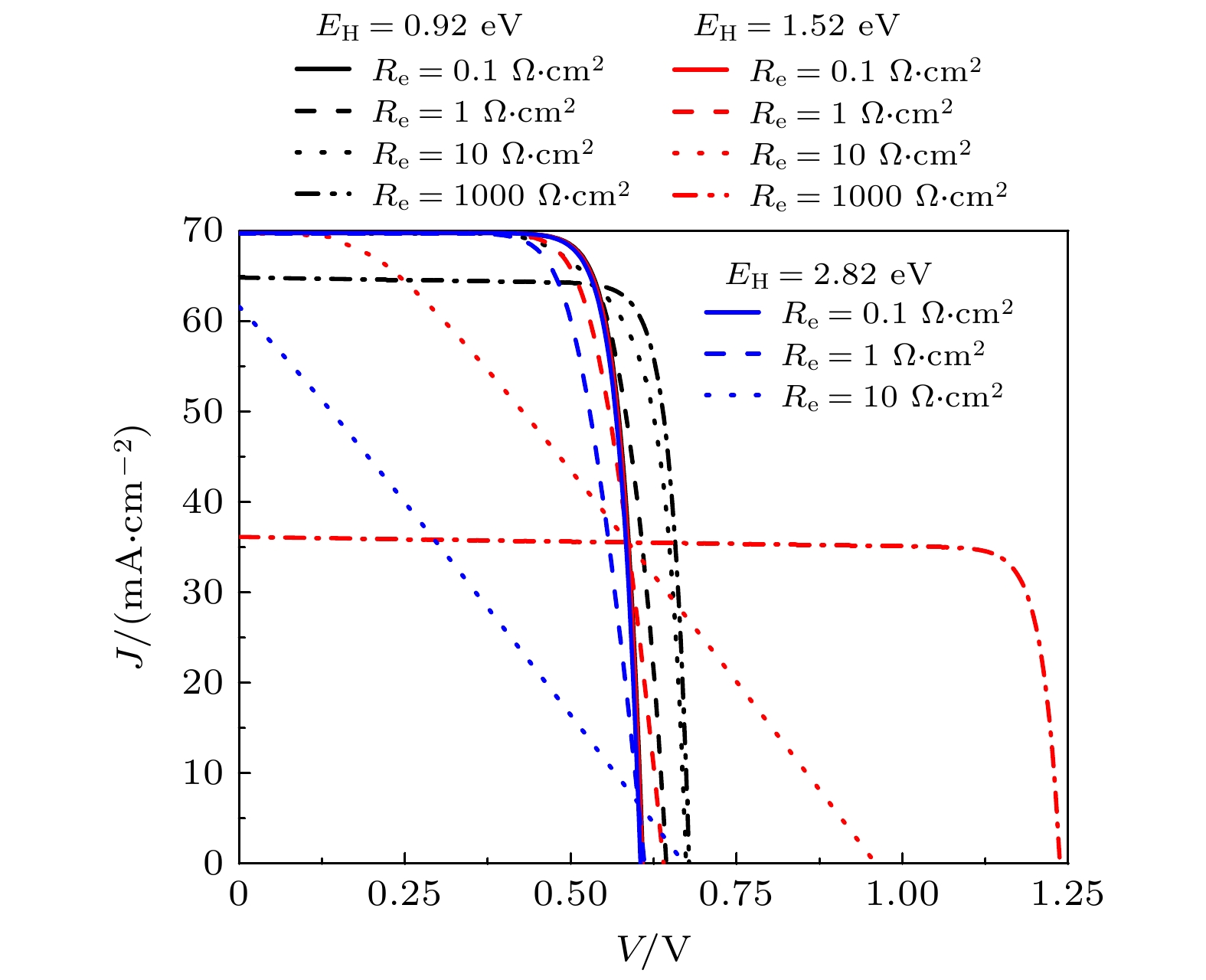
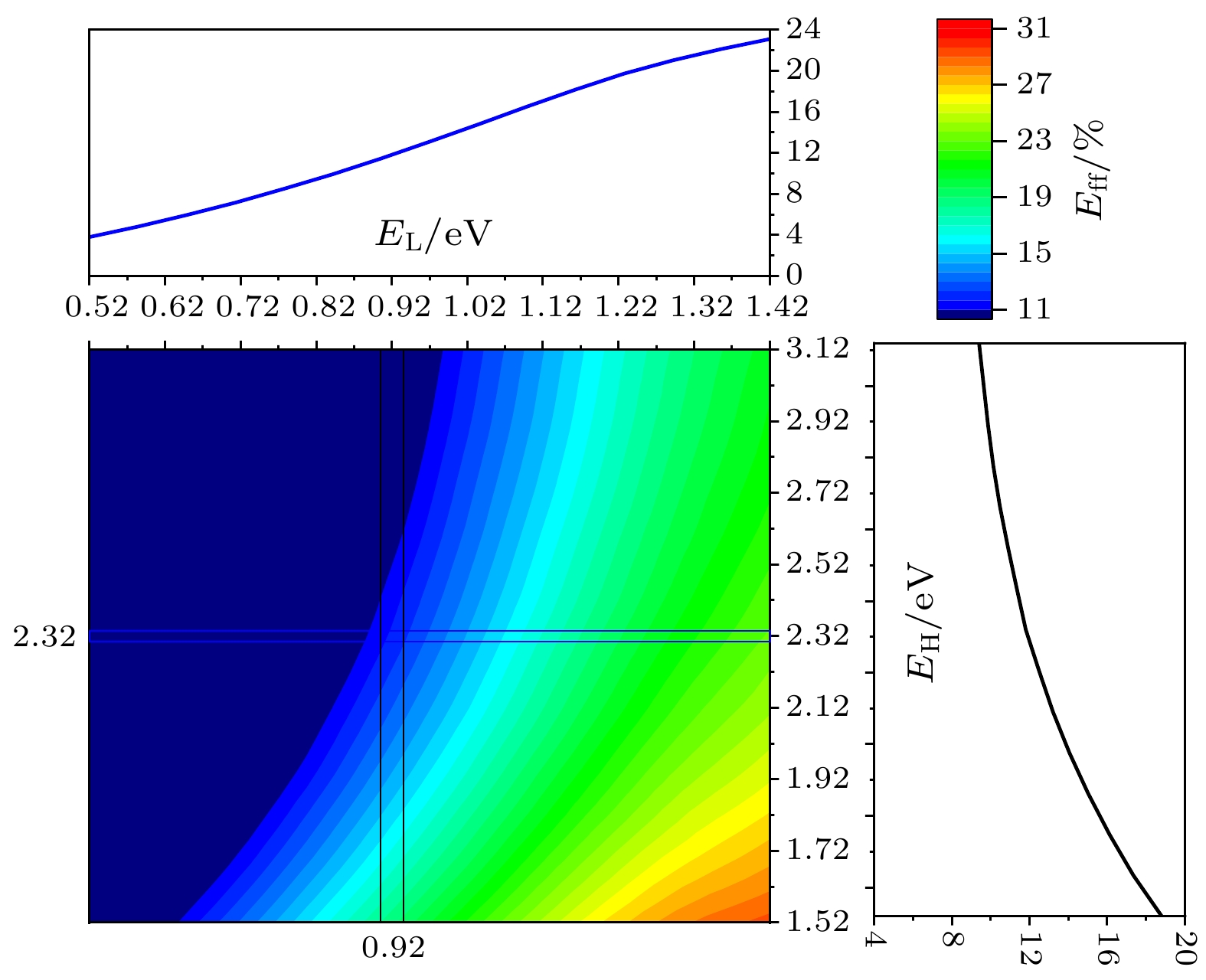
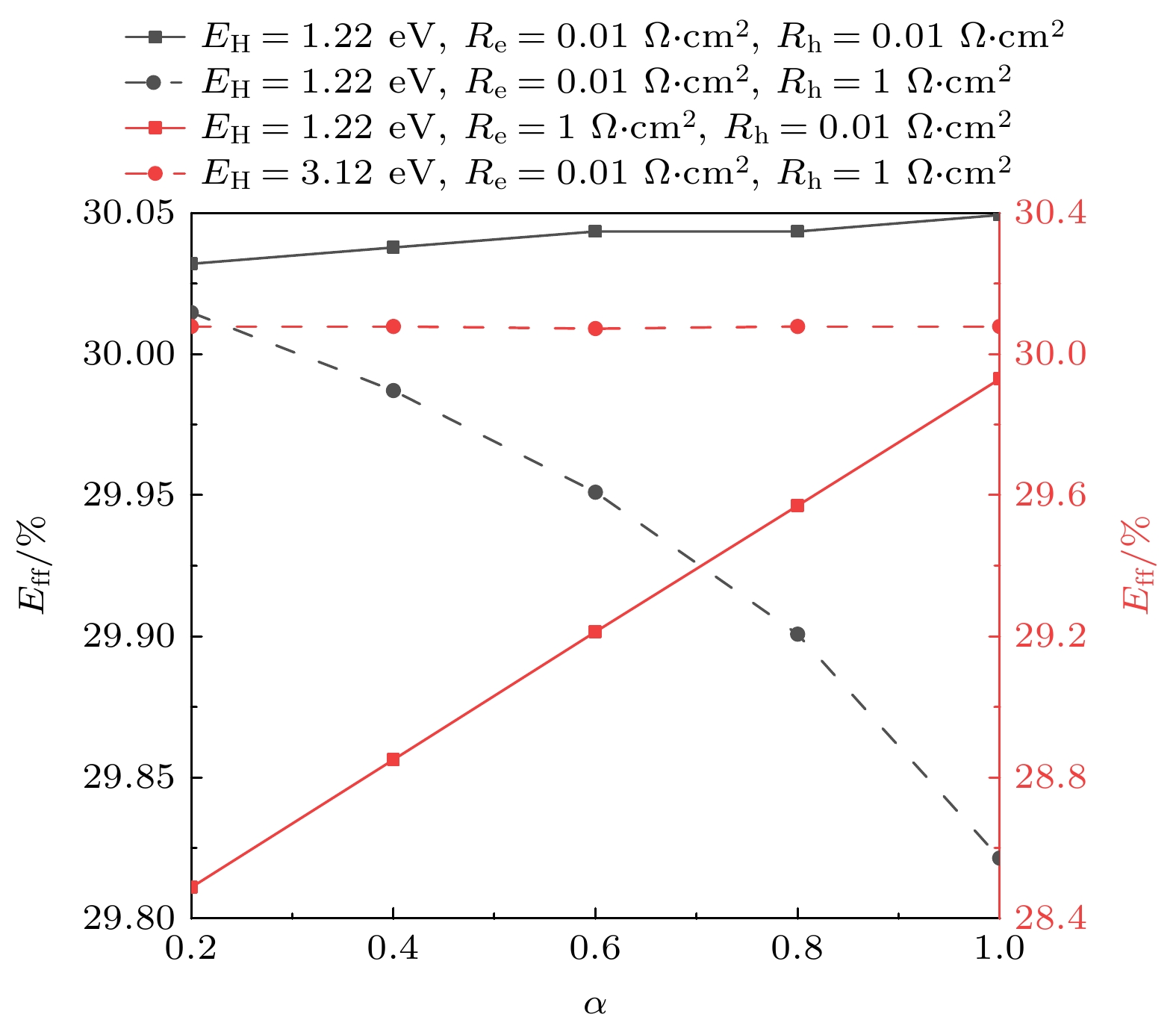
-
The ideal solar cell defined by the Shockley-Queisser (S-Q) theory is an important milestone in the analysis of photovoltaic devices based on some assumptions. One or more of the above assumptions are gradually avoided, and even exceed or approach the S-Q efficiency limit, so the development and improvement of S-Q theory is necessary. Heterojunction solar cells are one of the hot research fields in photovoltaics. In order to address the hindering effect of energy band discontinuity in the spatial barrier region of heterojunction solar cells on the transport of photogenerated carriers, the assumptions of S-Q theory based on the original S-Q theory of photovoltaic cells are revised in this work. The carrier mobility in the barrier region is assumed to be finite, and the infinite mobility in the S-Q model is abandoned. But the mobility in the N-type and the P-type neutral region are still infinite. The lumped relationship between carrier mobility and resistance in the barrier region is derived. Therefore, the physical process of charge transport is described in detail in this paper based on the continuity equation for semiconductors by considering the effect of absorption coefficients to prevent the quasi-Fermi level from crossing the conduction or valence band. Thus, the revised S-Q theoretical limit model of heterojunction solar cell is constructed. The diode equivalent circuit diagram is deduced and the photovoltaic conversion efficiency is evaluated eventually. The loss effects of charge transmission and band gap mismatch on the performance of heterojunction solar cells are analyzed in detail. The calculation results under the condition of 5780 K blackbody radiation and 300 K cell temperature with N-type wide bandgap (EH) and P-type narrow bandgap (EL) materials show that the highest conversion efficiency is about 31% with a hole resistance of 0.01 Ω·cm2 and electronic resistance of 0.01 Ω·cm2. The calculations show that the electronic resistance has a more negative and complicated effect on solar cell performance than hole resistance. When Re and Rh are small, the best conversion efficiency is in a range between 1.22 eV and 1.32 eV of the narrow bandgap. Increasing Re can increase the open circuit voltage of solar cells, but there are losses in efficiency and fill factor of solar cells. When Re is large enough, for example, Re = 1000 Ω·cm2, the open circuit voltage of solar cells is not limited by EL and can exceed the bandgap limit of the narrow bandgap material. Increasing Rh will also reduce efficiency, but the effect is not so great as Re. The change of absorption coefficient can cause the photogenerated current of L and H branches to change, and the radiation recombination losses of both branches can be regulated.
-
Keywords:
- Shockley-Queisser model /
- heterojunction solar cell /
- carrier mobility /
- absorptivity
[1] 沈文忠, 李正平 2014 硅基异质结太阳电池物理与器件(北京: 科学出版社) 第28页
Shen W Z, Li Z P 2014 Physics and Devices of Silicon Heterojunction Solar Cells (Beijing: Science Press) p28
[2] Li Y, Ru X N, Yang M, et al. 2024 Nature 626 105
Google Scholar
[3] Wang M H, Shi Y 2024 Sci. China Chem. 67 1117
Google Scholar
[4] Wang T Y, Deng W Q, Cao J P, Yan F 2023 Adv. Energy Mater. 13 2201436
Google Scholar
[5] 张美荣, 祝曾伟, 杨晓琴, 于同旭, 郁骁琦, 卢荻, 李顺峰, 周大勇, 杨辉 2023 物理学报 72 058801
Google Scholar
Zhang M R, Zhu Z W, Yang X Q, Yu T X, Yu X Q, Lu D, Li S F, Zhou D Y, Yang H 2023 Acta Phys. Sin. 72 058801
Google Scholar
[6] 王傲 2021 博士学位论文(南京: 南京理工大学)
Wang A 2021 Ph. D. Dissertation (Nanjing: Nanjing University of Science and Technology
[7] Li T H, Wang C, Hu C Z, Zhang N, Xiong Q, Zhang Z L, Li F, Zhang Y Y, Wu J H, Gao P 2024 Small Sci. 4 2300218
Google Scholar
[8] Zhao Y F, Procel P, Han C, et al. 2023 Sol. Energy Mater. Sol. Cells 258 112413
Google Scholar
[9] Long W, Yin S, Peng F G, Yang M, Fang L, Ru X N, Qu M H, Lin H F, Xu X X 2021 Sol. Energy Mater. Sol. Cells 231 111291
Google Scholar
[10] Jiang K, Zhang H H, Zhang L P, Meng F Y, Gao Y F, Yu X R, Zhao D M, Li R, Huang H W, Hao Z D, Liu Z X, Liu W Z 2023 Sci. China Mater. 66 4891
Google Scholar
[11] Shockley W, Queisser H J 1961 J. Appl. Phys. 32 510
Google Scholar
[12] Ahmad F, Lakhtakia A, Monk P B 2020 Appl. Phys. Lett. 117 033901
Google Scholar
[13] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2019 Nat. Photonics 13 501
Google Scholar
[14] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2021 Nat. Photonics 15 165
Google Scholar
[15] Markvart T 2021 Nat. Photonics 15 163
Google Scholar
[16] Marti A 2019 IEEE J. Photovolt. 9 1590
Google Scholar
[17] 熊超, 陈磊, 袁洪春, 姚若河 2013 太阳能学报 34 746
Xiong C, Chen L, Yuan H C, Yao R H 2013 Acta Energ. Sol. Sin. 34 746
[18] Anderson R L 1962 Solid-State Electron. 5 341
Google Scholar
[19] Qian C, Bai Y, Ye H R, Chen Y, Ye L, Zhang C, Ma Z, Chen T, Fan H L, Huang Y L, Liu W Z, Yu J S, Yu J 2024 Sol. Energy 274 112585
Google Scholar
[20] 刘恩科, 朱秉升, 罗晋生 2008 半导体物理学(第7版) (北京: 电子工业出版社) 第148页
Liu E K, Zhu B S, Luo J S 2008 The Physics of Semiconductors (7th Ed.) (Beijing: Publishing House of Electronics Industry) p148
-
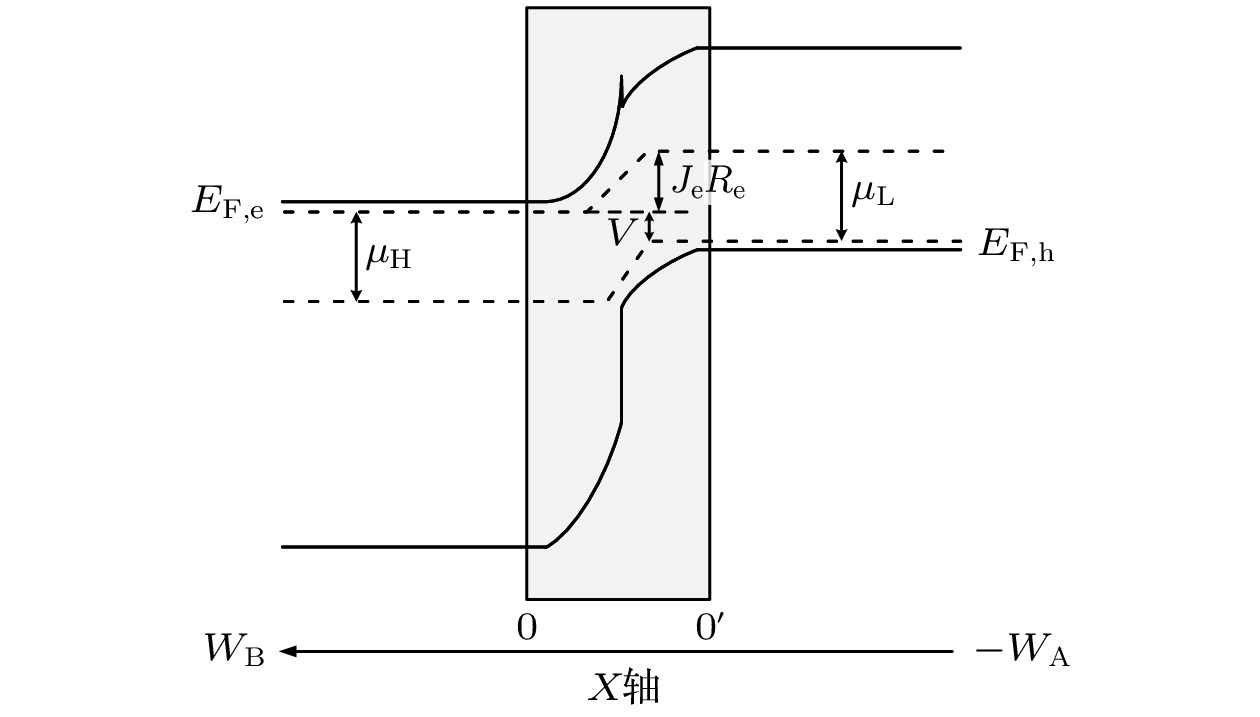
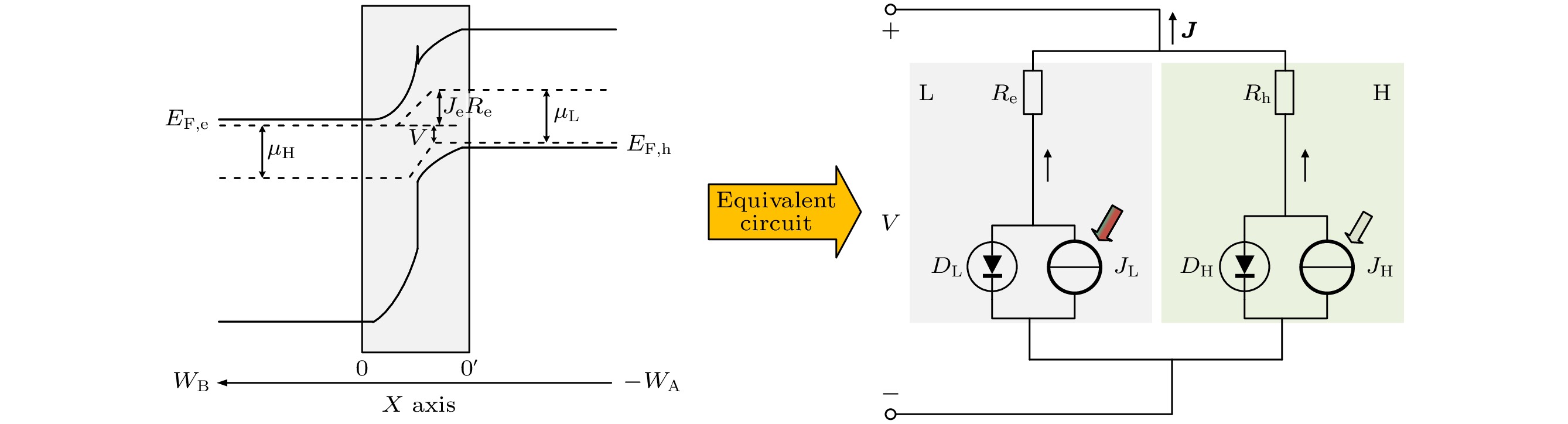
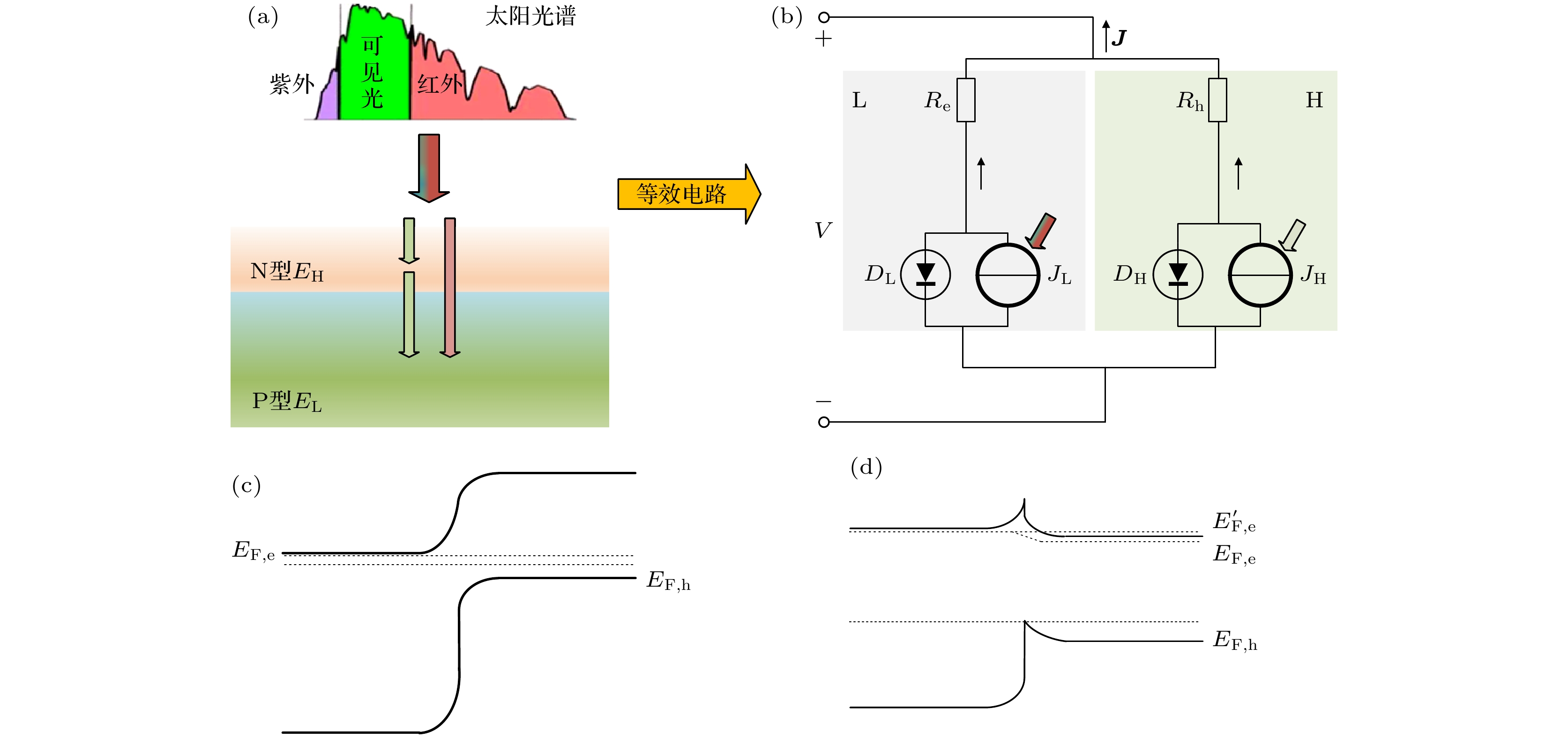
图 1 (a)异质结结构图; (b)异质结等效电路图; (c)适当电压、无限迁移率能带分布; (d)大电压、无限/有限迁移率能带分布; 这里Re为对电子的电阻(Ω·cm2), Rh为对空穴的电阻(Ω·cm2), DL, DH为窄带隙、宽带隙材料等效二极管, JL和JH为窄带隙、宽带隙材料产生的光生电流
Figure 1. (a) Heterojunction structure diagram; (b) heterojunction equivalent circuit diagram; (c) infinite mobility band distribution under appropriate voltage; (d) infinite/finite mobility band distribution under high voltage. Re is the resistance to electrons (Ω·cm2), and Rh is the resistance to holes (Ω·cm2). DL and DH are equivalent diodes made of narrow bandgap and wide bandgap materials. JL and JH are photocurrent generated by narrow bandgap and wide bandgap materials, respectively.
图 2 有限迁移率条件下能带图
Figure 2. Energy band diagram under limited mobility conditions.
图 3 Eff分布图(α = 1, Rh = 0.01 Ω·cm2, Re = 0.01 Ω·cm2, EH = 1.52—3.12 eV , EL = 0.52—1.42 eV)
Figure 3. Eff profile (α = 1, Rh = 0.01 Ω·cm2, Re = 0.01 Ω·cm2, EH = 1.52—3.12 eV , EL = 0.52—1.42 eV).
图 4 I-V曲线(α = 1, EL = 0.82 eV, EH = 0.92, 1.52, 2.82 eV, Rh = 0.01 Ω·cm2, Re = 0.1, 1, 10, 1000 Ω·cm2)
Figure 4. I-V curves (α = 1, EL = 0.82 eV, EH = 0.92, 1.52, 2.82 eV, Rh = 0.01 Ω·cm2, Re = 0.1, 1, 10, 1000 Ω·cm2).
图 5 Eff分布图(α = 1, Rh = 0.01Ω·cm2, Re = 1 Ω·cm2, EH = 1.52—3.12 eV, EL = 0.52—1.42 eV)
Figure 5. Eff profile (α = 1, Rh = 0.01 Ω·cm2, Re = 1 Ω·cm2, EH = 1.52–3.12 eV, EL = 0.52–1.42 eV).
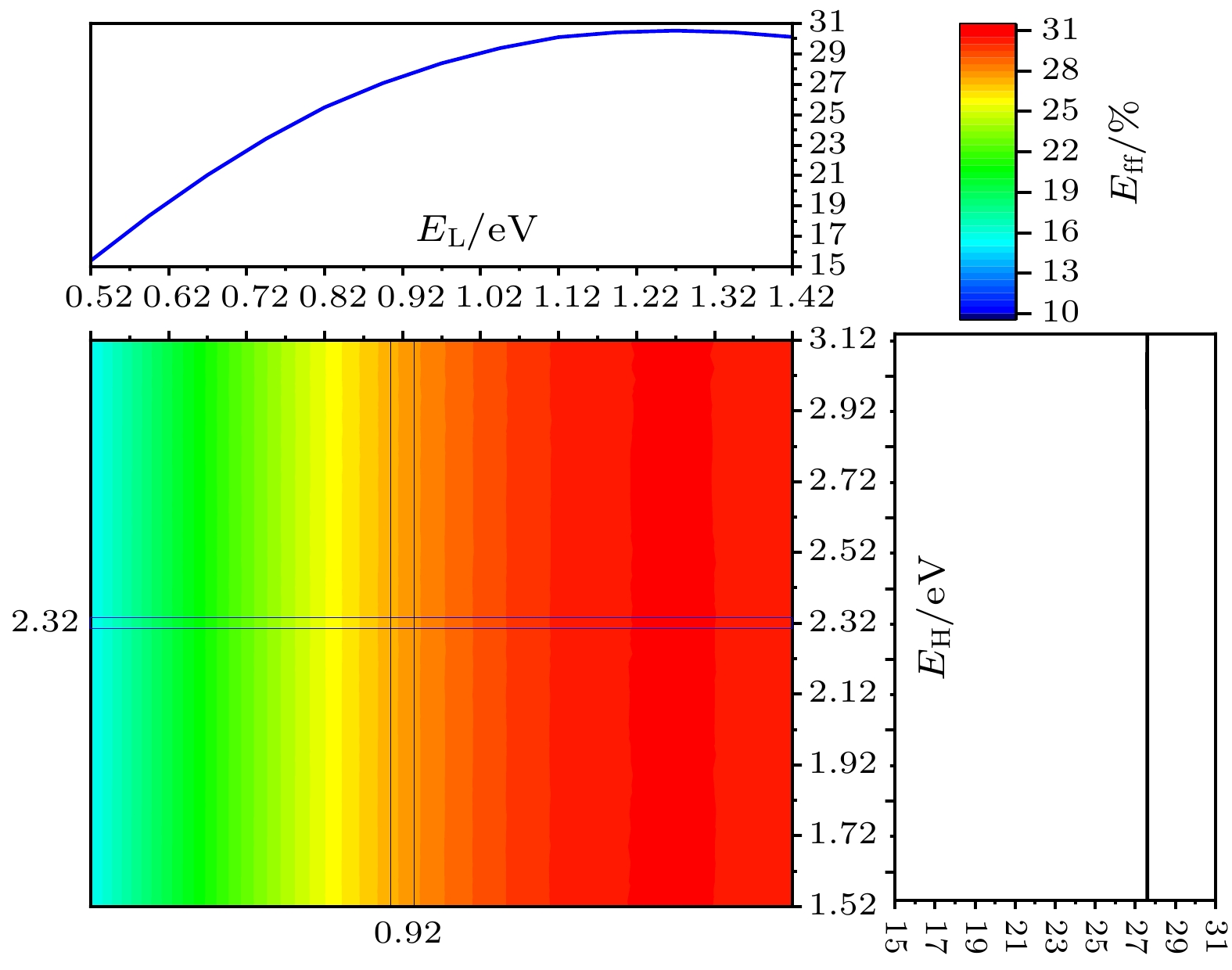
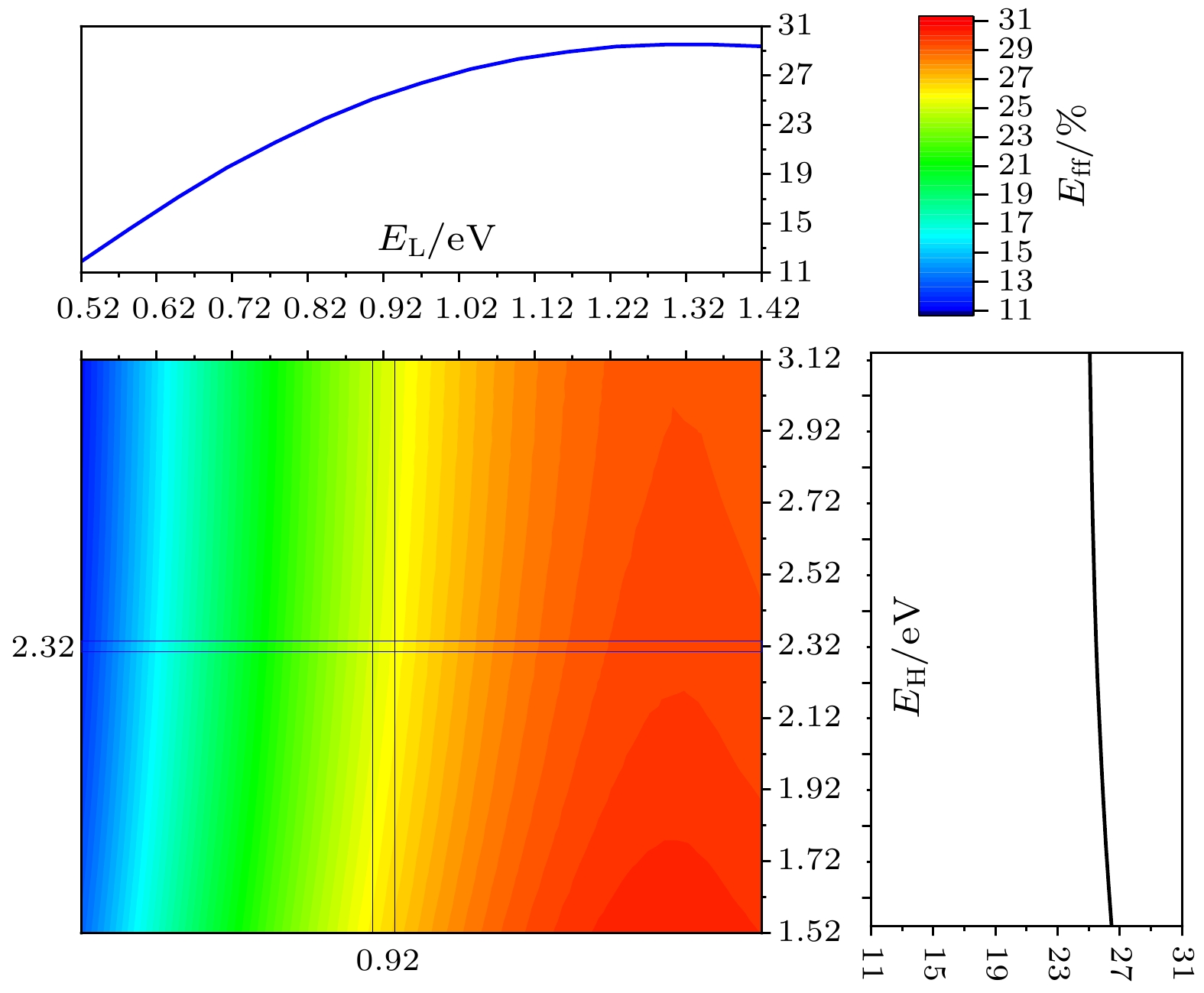
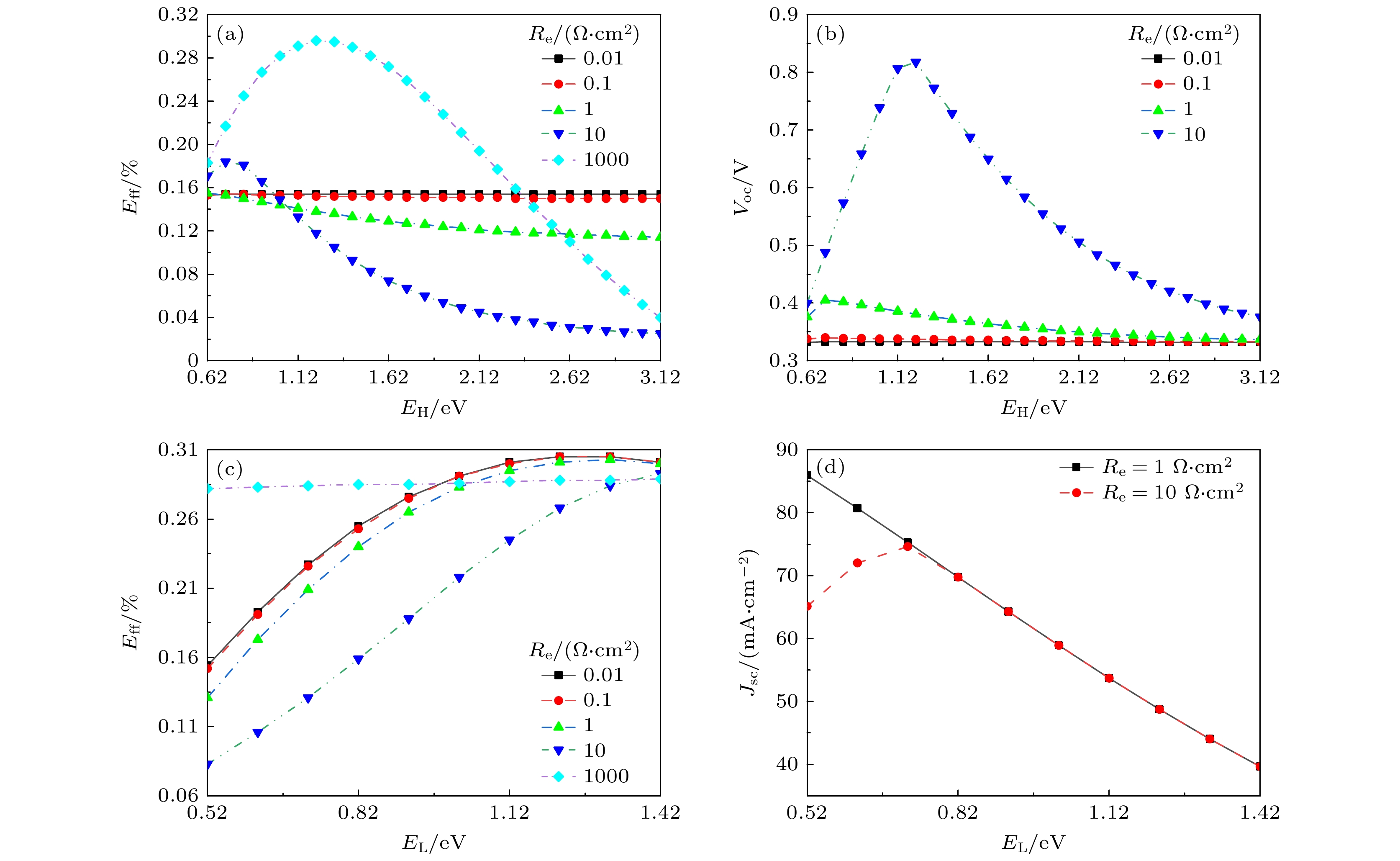
图 6 (a) Eff -EH曲线(Rh = 0.01 Ω·cm2, EL = 0.52 eV); (b) Voc -EH曲线(Rh = 0.01 Ω·cm2, EL = 0.52 eV); (c) Eff -EL曲线(Rh = 0.01 Ω·cm2, EH = 1.52 eV); (d) Jsc -EL曲线(Rh = 0.01 Ω·cm2, EH = 1.52 eV)
Figure 6. (a) Eff -EH curves (Rh = 0.01 Ω·cm2, EL = 0.52 eV); (b) Voc -EH curves (Rh = 0.01 Ω·cm2, EL = 0.52 eV); (c) Eff -EL curves (Rh = 0.01 Ω·cm2, EH = 1.52 eV); (d) Jsc -EL curves (Rh = 0.01 Ω·cm2, EH = 1.52 eV).
图 7 Eff分布图(α = 1, Rh = 0.01 Ω·cm2, Re = 10 Ω·cm2, EH = 1.52—3.12 eV, EL = 0.52—1.42 eV)
Figure 7. Eff profile (α = 1, Rh = 0.01Ω·cm2, Re = 10 Ω·cm2, EH = 1.52–3.12 eV, EL = 0.52–1.42 eV).
图 8 Eff -Re曲线
Figure 8. Eff -Re curves.
图 9 (a) Eff -EH曲线(EL = 1.12 eV, Re = 0.01 Ω·cm2); (b) Eff -Rh曲线
Figure 9. (a) Eff -EH curves (EL = 1.12 eV, Re = 0.01 Ω·cm2); (b) Eff -Rh curves.
图 10 Eff -α曲线(EL = 1.12 eV)
Figure 10. Eff -α curves (EL = 1.12 eV).
-
[1] 沈文忠, 李正平 2014 硅基异质结太阳电池物理与器件(北京: 科学出版社) 第28页
Shen W Z, Li Z P 2014 Physics and Devices of Silicon Heterojunction Solar Cells (Beijing: Science Press) p28
[2] Li Y, Ru X N, Yang M, et al. 2024 Nature 626 105
Google Scholar
[3] Wang M H, Shi Y 2024 Sci. China Chem. 67 1117
Google Scholar
[4] Wang T Y, Deng W Q, Cao J P, Yan F 2023 Adv. Energy Mater. 13 2201436
Google Scholar
[5] 张美荣, 祝曾伟, 杨晓琴, 于同旭, 郁骁琦, 卢荻, 李顺峰, 周大勇, 杨辉 2023 物理学报 72 058801
Google Scholar
Zhang M R, Zhu Z W, Yang X Q, Yu T X, Yu X Q, Lu D, Li S F, Zhou D Y, Yang H 2023 Acta Phys. Sin. 72 058801
Google Scholar
[6] 王傲 2021 博士学位论文(南京: 南京理工大学)
Wang A 2021 Ph. D. Dissertation (Nanjing: Nanjing University of Science and Technology
[7] Li T H, Wang C, Hu C Z, Zhang N, Xiong Q, Zhang Z L, Li F, Zhang Y Y, Wu J H, Gao P 2024 Small Sci. 4 2300218
Google Scholar
[8] Zhao Y F, Procel P, Han C, et al. 2023 Sol. Energy Mater. Sol. Cells 258 112413
Google Scholar
[9] Long W, Yin S, Peng F G, Yang M, Fang L, Ru X N, Qu M H, Lin H F, Xu X X 2021 Sol. Energy Mater. Sol. Cells 231 111291
Google Scholar
[10] Jiang K, Zhang H H, Zhang L P, Meng F Y, Gao Y F, Yu X R, Zhao D M, Li R, Huang H W, Hao Z D, Liu Z X, Liu W Z 2023 Sci. China Mater. 66 4891
Google Scholar
[11] Shockley W, Queisser H J 1961 J. Appl. Phys. 32 510
Google Scholar
[12] Ahmad F, Lakhtakia A, Monk P B 2020 Appl. Phys. Lett. 117 033901
Google Scholar
[13] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2019 Nat. Photonics 13 501
Google Scholar
[14] Guillemoles J F, Kirchartz T, Cahen D, Rau U 2021 Nat. Photonics 15 165
Google Scholar
[15] Markvart T 2021 Nat. Photonics 15 163
Google Scholar
[16] Marti A 2019 IEEE J. Photovolt. 9 1590
Google Scholar
[17] 熊超, 陈磊, 袁洪春, 姚若河 2013 太阳能学报 34 746
Xiong C, Chen L, Yuan H C, Yao R H 2013 Acta Energ. Sol. Sin. 34 746
[18] Anderson R L 1962 Solid-State Electron. 5 341
Google Scholar
[19] Qian C, Bai Y, Ye H R, Chen Y, Ye L, Zhang C, Ma Z, Chen T, Fan H L, Huang Y L, Liu W Z, Yu J S, Yu J 2024 Sol. Energy 274 112585
Google Scholar
[20] 刘恩科, 朱秉升, 罗晋生 2008 半导体物理学(第7版) (北京: 电子工业出版社) 第148页
Liu E K, Zhu B S, Luo J S 2008 The Physics of Semiconductors (7th Ed.) (Beijing: Publishing House of Electronics Industry) p148
DownLoad:
Catalog
Metrics
- Abstract views: 299
- PDF Downloads: 18
- Cited By: 0
