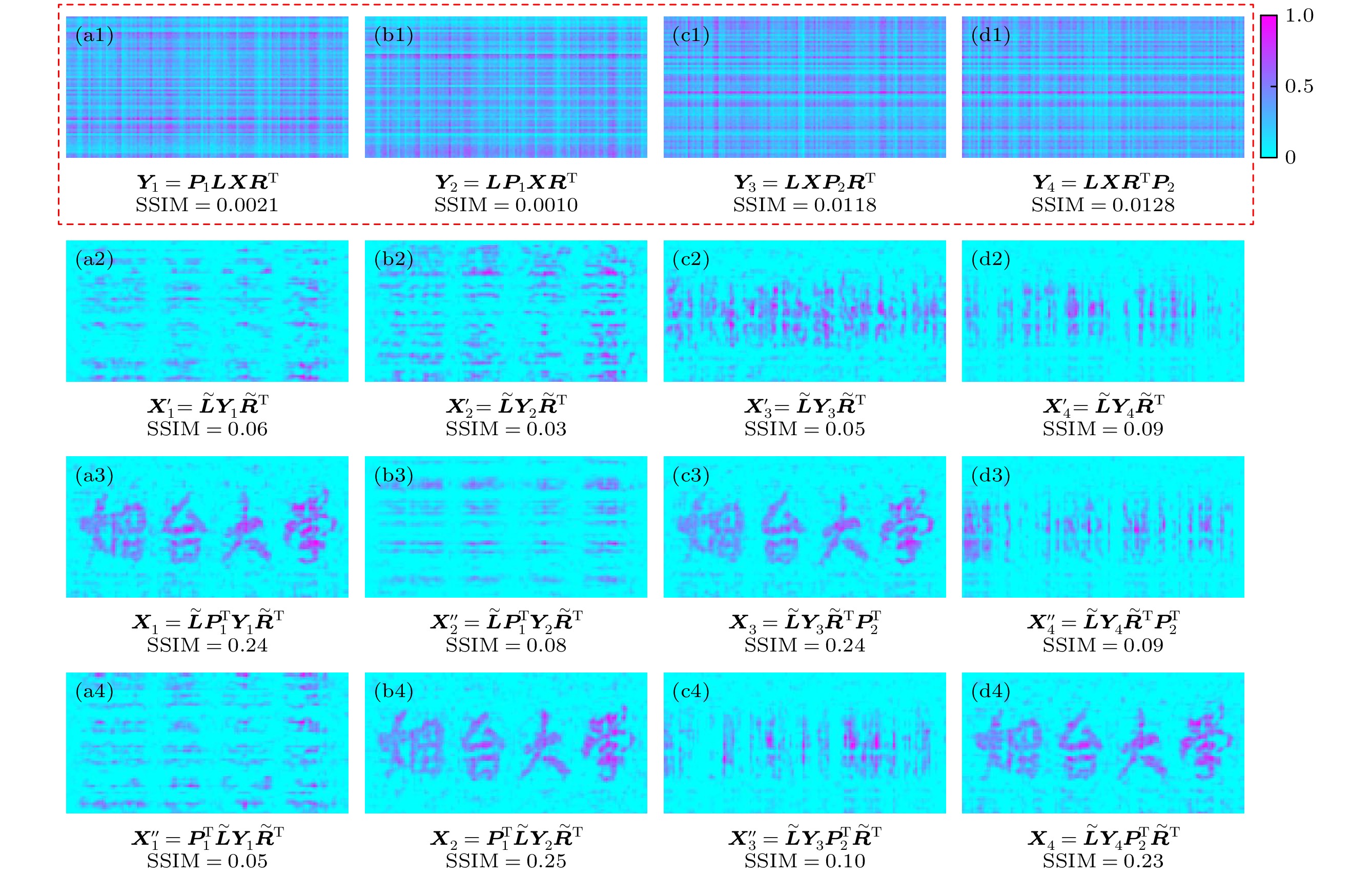
-
Ghost imaging is closely related to image encryption, since the random speckle patterns are often utilized. In the two-dimensional (2D) case, computational ghost imaging can be realized through $ \boldsymbol{L}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}=\boldsymbol{Y} $, where $ \boldsymbol{X} $ is a 2D object, $ \boldsymbol{Y} $ is the bucket detection signals reshaped into a 2D form, and $ \boldsymbol{L} $ and $ \boldsymbol{R} $ are two random matrices. In this work, a scenario of flexible image encryption in ghost imaging in the 2D case is proposed. The image is encrypted into the bucket detection signals by arbitrarily arranging the two random matrices ($ \boldsymbol{L} $ and $ \boldsymbol{R} $) and other two permutation matrices ($ {\boldsymbol{P}}_{1} $ and $ {\boldsymbol{P}}_{2} $). The permutation matrices are used to disrupt the distribution of the bucket signals. Considering that the specific size of the image may not be square but rectangle, eight ways of image encryption are investigated in this work. Four of them use only one permutation matrix ($ {\boldsymbol{P}}_{1} $ or $ {\boldsymbol{P}}_{2} $), and they are $ {\boldsymbol{P}}_{1}\boldsymbol{L}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}={\boldsymbol{Y}}_{1} $, $ \boldsymbol{L}{\boldsymbol{P}}_{1}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}={\boldsymbol{Y}}_{2} $, $ \boldsymbol{L}\boldsymbol{X}{\boldsymbol{P}}_{2}{\boldsymbol{R}}^{\mathrm{T}}={\boldsymbol{Y}}_{3} $, $ \boldsymbol{L}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}{\boldsymbol{P}}_{2}={\boldsymbol{Y}}_{4} $. The other four use two permutation matrices ($ {\boldsymbol{P}}_{1} $ and $ {\boldsymbol{P}}_{2} $), and they are $ {\boldsymbol{P}}_{1}\boldsymbol{L}\boldsymbol{X}{\boldsymbol{P}}_{2}{\boldsymbol{R}}^{\mathrm{T}}={\boldsymbol{Y}}_{5} $, $ {\boldsymbol{P}}_{1}\boldsymbol{L}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}{\boldsymbol{P}}_{2}={\boldsymbol{Y}}_{6} $, $ \boldsymbol{L}{\boldsymbol{P}}_{1}\boldsymbol{X}{\boldsymbol{P}}_{2}{\boldsymbol{R}}^{\mathrm{T}}={\boldsymbol{Y}}_{7} $, and $ \boldsymbol{L}{\boldsymbol{P}}_{1}\boldsymbol{X}{\boldsymbol{R}}^{\mathrm{T}}{\boldsymbol{P}}_{2}={\boldsymbol{Y}}_{8} $. Specifically, in experiment, the measurement matrix is generated by the Kronecker product of the random matrices and permutation matrices. According to the 8 ways of image encryption, the 8 measurement matrices are $ {\boldsymbol{A}}_{1}=\left({\boldsymbol{P}}_{1}\boldsymbol{L}\right)\otimes \boldsymbol{R}, $ $ {\boldsymbol{A}}_{2}=\left(\boldsymbol{L}{\boldsymbol{P}}_{1}\right)\otimes \boldsymbol{R}, $ $ {\boldsymbol{A}}_{3}=\boldsymbol{L}\otimes \left(\boldsymbol{R}{\boldsymbol{P}}_{2}^{\mathrm{T}}\right) $, $ {\boldsymbol{A}}_{4}=\boldsymbol{L}\otimes \left({\boldsymbol{P}}_{2}^{\mathrm{T}}\boldsymbol{R}\right) $, $ {\boldsymbol{A}}_{5}=\left({\boldsymbol{P}}_{1}\boldsymbol{L}\right)\otimes \left(\boldsymbol{R}{\boldsymbol{P}}_{2}^{\mathrm{T}}\right) $, $ {\boldsymbol{A}}_{6}=\left({\boldsymbol{P}}_{1}\boldsymbol{L}\right)\otimes $$ \left({\boldsymbol{P}}_{2}^{\mathrm{T}}\boldsymbol{R}\right) $, $ {\boldsymbol{A}}_{7}=\left(\boldsymbol{L}{\boldsymbol{P}}_{1}\right)\otimes \left(\boldsymbol{R}{\boldsymbol{P}}_{2}^{\mathrm{T}}\right) $, and $ {\boldsymbol{A}}_{8}=\left(\boldsymbol{L}{\boldsymbol{P}}_{1}\right)\otimes \left({\boldsymbol{P}}_{2}^{\mathrm{T}}\boldsymbol{R}\right) $. These measurement matrices are used to form the random speckle patterns which are then projected onto the object. A spatial light modulator (SLM) is employed to load the objects and random speckle patterns. A charge coupled device (CCD) is used to obtain the bucket detection signals. As truncated singular value decomposition (TSVD) is an effective denoising method, it is used to obtain the pseudoinverse matrices of the random matrices used in the decryption process. Only when the pseudoinverse matrices of the random matrices, as well as the correct sequences of the random and permutation matrices, are known in each way, can the image be successfully decrypted. Otherwise, image decryption will not be successful. The structural similarity (SSIM), peak signal-to-noise ratio (PSNR), and correlation coefficient (CC) are used to evaluate the quality of the decrypted images. The SSIMs of object and the 2D bucket detection signals are very low, indicating the successful encryption. The PSNRs and CCs of the successful decrypted images are better than those of unsuccessful images. The successfully decrypted images clearly reconstruct the image of the object, while the unsuccessful images are in a mess. Our method provides a new idea of image encryption in ghost imaging, and image encryption is therefore enhanced and made flexible. Moreover, the present protocol can be combined with other image encryption techniques to form a more flexible protocol, which also has some application prospects in other image processing such as watermarking and image hiding. -
Keywords:
- ghost imaging /
- permutation encryption /
- Kronecker product
-
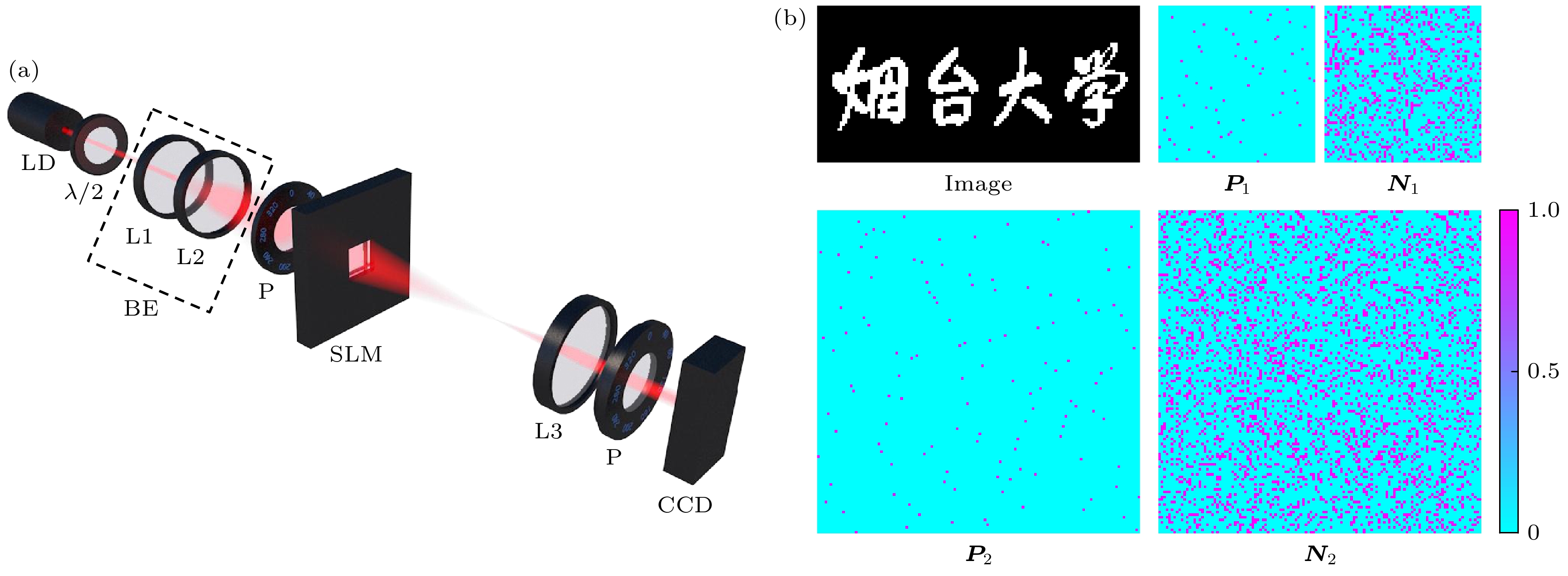
图 1 (a)实验装置图(LD, 激光二极管; λ/2, 半波片; BE, 扩束器; P, 偏振片; L1, L2, L3, 透镜; SLM, 空间光调制器; CCD, 电荷耦合器件); (b)物体图像($ \boldsymbol{X} $: $ 64\times 128 $)、两个随机矩阵($ \boldsymbol{L}={\boldsymbol{N}}_{1} $: $ 64\times 64 $和$ \boldsymbol{R}={\boldsymbol{N}}_{2} $: $ 128\times 128 $)、两个置换矩阵($ {\boldsymbol{P}}_{1} $: $ 64\times 64 $, $ {\boldsymbol{P}}_{2} $: $ 128\times 128 $)
Figure 1. (a) Experimental setup (LD, laser diode; λ/2, half waveplate; BE, beam expander; P, polarizer; L1, L2, L3, lenses; SLM, spatial light modulator; CCD, charge coupled device); (b) image ($ \boldsymbol{X} $: $ 64\times 128 $), two random matrices ($ \boldsymbol{L}={\boldsymbol{N}}_{1} $: $ 64\times 64 $ and $ \boldsymbol{R}={\boldsymbol{N}}_{2} $: $ 128\times 128 $), and two permutation matrices ($ {\boldsymbol{P}}_{1} $: $ 64\times 64 $, $ {\boldsymbol{P}}_{2} $: $ 128\times 128 $).
图 2 使用一个置换矩阵时的加密解密图像 (a1)—(d1) 加密图像; (a2)—(d4) 解密图像. 使用的加密或解密公式标在图片下方
Figure 2. Encrypted and decrypted images with one permutation matrix: (a1)–(d1) Encrypted images; (a2)–(d4) decrypted images. The encryped or decrypted equations are marked below the pictures.
图 3 使用两个置换矩阵时的加密解密图像 (a1)—(d1) 加密图像; (a2)—(d6) 解密图像. 使用的加密或解密公式标在图片下方
Figure 3. Encrypted and decrypted images with two permutation matrices: (a1)–(d1) Encrypted images; (a2)–(d6) decrypted images. The encryped or decrypted equations are marked below the pictures.
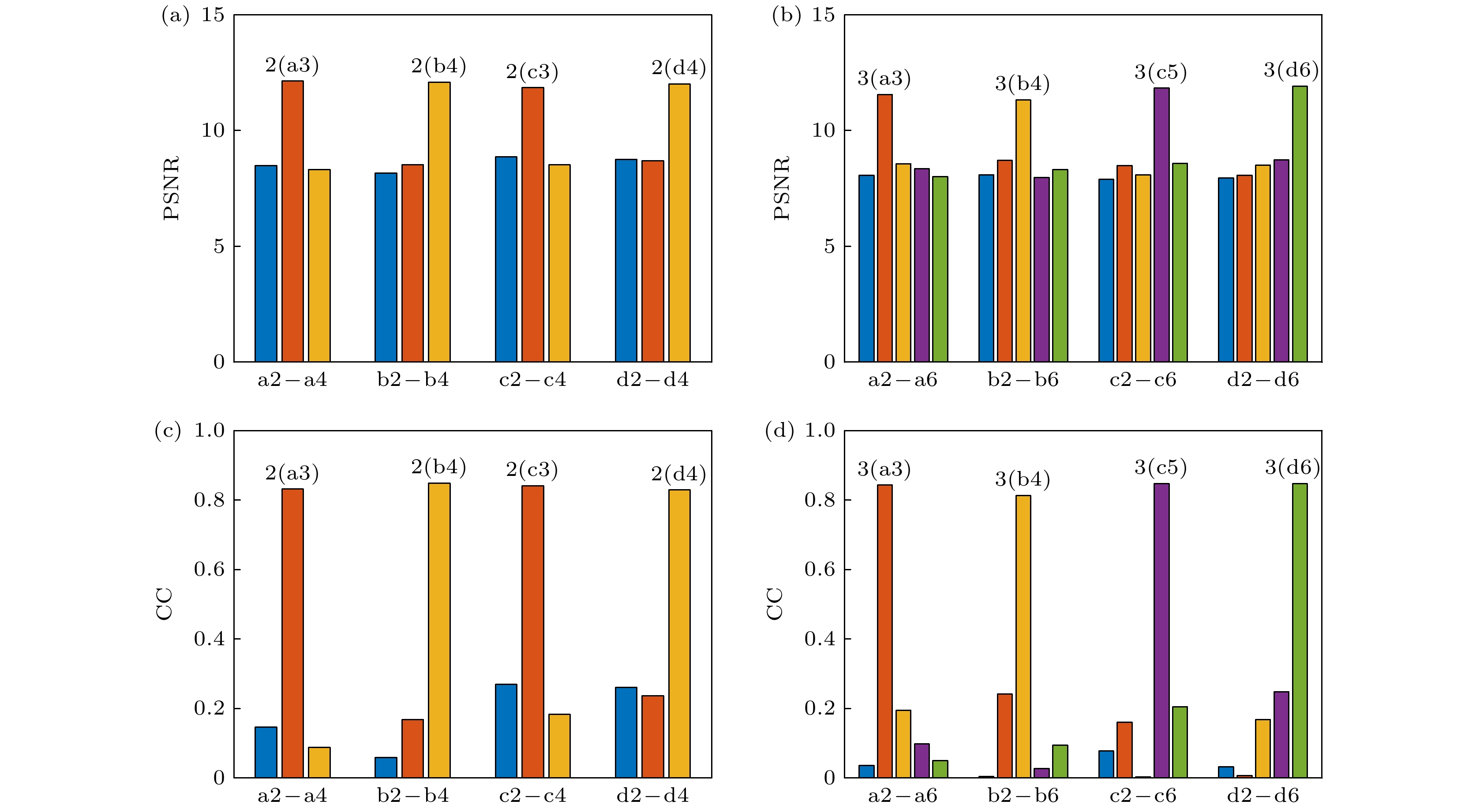
图 4 解密图像的PSNR和CC值 (a)图2中解密图像的PSNR值; (b)图3中解密图像的PSNR值; (c)图2中解密图像的CC值; (d)图3中解密图像的CC值
Figure 4. PSNRs and CCs of the decrypted images: (a) PSNRs of the decrypted images in Fig. 2; (b) PSNRs of the decrypted images in Fig. 3; (c) CCs of the decrypted images in Fig. 2; (d) CCs of the decrypted images in Fig. 3.
-
[1] Shapiro J H 2008 Phys. Rev. A 78 061802
Google Scholar
[2] Cao D Z, Xiong J, Zhang S H, Lin L F, Gao L, Wang K 2008 Appl. Phys. Lett. 92 201102
Google Scholar
[3] Chan K W C, O’Sullivan M N, Boyd R W 2009 Opt. Lett. 34 3343
Google Scholar
[4] Bromberg Y, Katz O, Silberberg Y 2009 Phys. Rev. A 79 053840
Google Scholar
[5] Romberg J 2008 IEEE Signal Process. Mag. 25 14
[6] Katz O, Bromberg Y, Silberberg Y 2009 Appl. Phys. Lett. 95 131110
Google Scholar
[7] Zhang C, Guo S, Cao J, Guan J, Gao F 2014 Opt. Express 22 30063
Google Scholar
[8] Gong W 2015 Photonics Res. 3 234
Google Scholar
[9] Zhang X, Meng X, Yang X, Wang Y, Yin Y, Li X, Peng X, He W, Dong G, Chen H 2018 Opt. Express 26 12948
Google Scholar
[10] Lv X, Guo S, Wang C, Yang C, Zhang H, Song J, Gong W, Gao F 2018 IEEE Photonics J. 10 3900708
[11] Luo B, Yin P, Yin L, Wu G, Guo H 2018 Opt. Express 26 23093
Google Scholar
[12] Nie X, Zhao X, Peng T, Scully M O 2022 Phys. Rev. A 105 043525
Google Scholar
[13] Lyu M, Wang W, Wang H, Wang H, Li G, Chen N, Situ G 2017 Sci. Rep. 7 17865
Google Scholar
[14] Barbastathis G, Ozcan A, Situ G 2019 Optica 6 921
Google Scholar
[15] Zhang X, Ren Y, Feng G, Qian Z 2011 Seventh International Conference on Intelligent Information Hiding and Multimedia Signal Processing Dalian, China, October 14–16, 2011 pp222–225
[16] Kong L J, Li Y, Qian S X, Li S M, Tu C, Wang H T 2013 Phys. Rev. A 88 013852
Google Scholar
[17] Chen W, Chen X 2013 Appl. Phys. Lett. 103 221106
Google Scholar
[18] Zhang Y, Zhao S 2017 Chin. Phys. B 26 054205
Google Scholar
[19] Wu J, Xie Z, Liu Z, Liu W, Zhang Y, Liu S 2016 Opt. Commun. 359 38
Google Scholar
[20] Shi D, Huang J, Wang Y, Yuan K, Xie C, Liu D, Zhu W 2017 Sci. Rep. 7 13172
Google Scholar
[21] Zhu J, Yang X, Meng X, Wang Y, Yin Y, Sun X, Dong G 2018 Opt. Commun. 420 34
Google Scholar
[22] Kang Y, Zhang L, Zhang D 2018 Opt. Lasers Eng. 111 58
Google Scholar
[23] Liu Y, Zheng P, Liu H C 2022 Opt. Express 30 14073
Google Scholar
[24] Liu J F, Dong Y, Wang L, Zhao S M 2023 Chin. Phys. B 32 074202
Google Scholar
[25] Zhao Y N, Chen L S, Chen L Y, Kong L, Wang C, Ren C, Zhang S H, Cao D Z 2024 Opt. Lasers Eng. 181 108408
Google Scholar
[26] Albert A 1972 Regression and the Moore-Penrose pseudoinverse (New York: Academic Press
[27] Chen L Y, Wang C, Xiao X Y, Ren C, Zhang D J, Li Z, Cao D Z 2022 Opt. Express 30 6248
Google Scholar
[28] Zhou W, Bovik A C, Sheikh H R, Simoncelli E P 2004 IEEE Trans. Image Process. 13 600
Google Scholar
[29] Qu G, Meng X, Yang X, Wu H, Wang P, He W, Chen H 2021 Opt. Lasers Eng. 137 106376
Google Scholar
[30] Wang L, Zhao S, Cheng W, Gong L, Chen H 2016 Opt. Commun. 366 314
Google Scholar
[31] Qu G, Meng X, Yin Y, Wu H, Yang X, Peng X, He W 2021 Opt. Lasers Eng. 137 106392
Google Scholar
[32] Huang H, Han Z 2024 Results Phys. 56 107282
Google Scholar
DownLoad:
Metrics
- Abstract views: 298
- PDF Downloads: 3
- Cited By: 0
