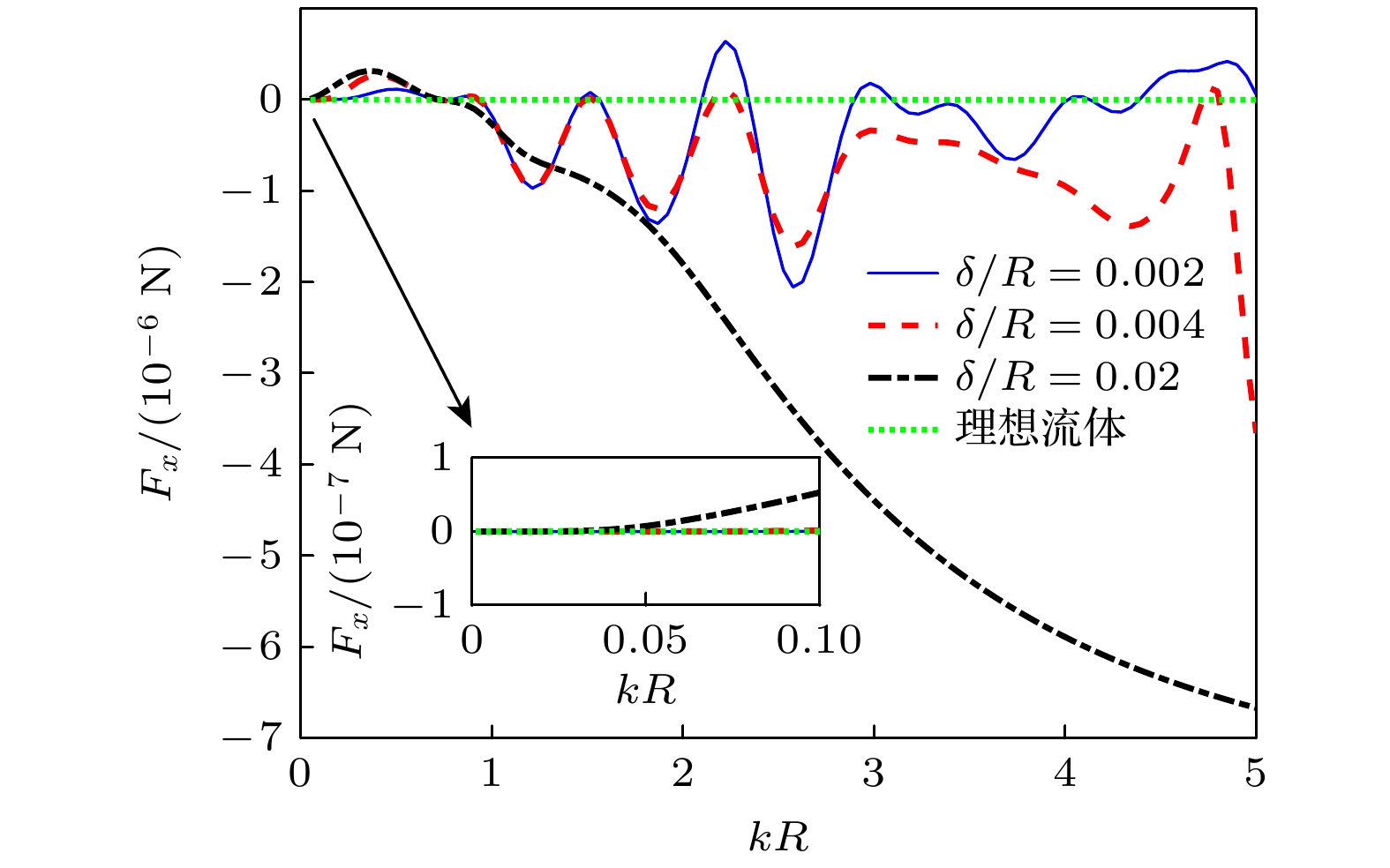
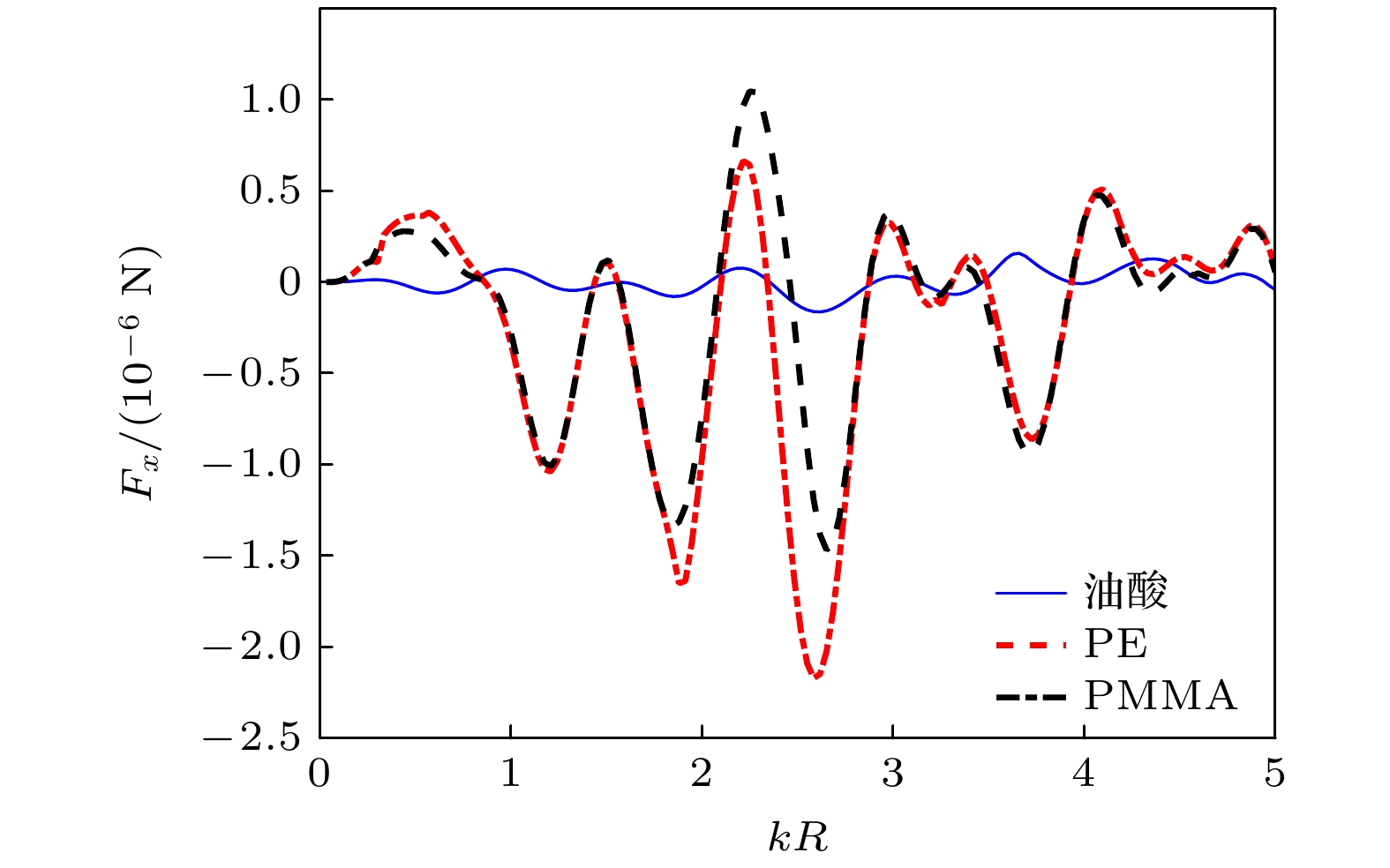
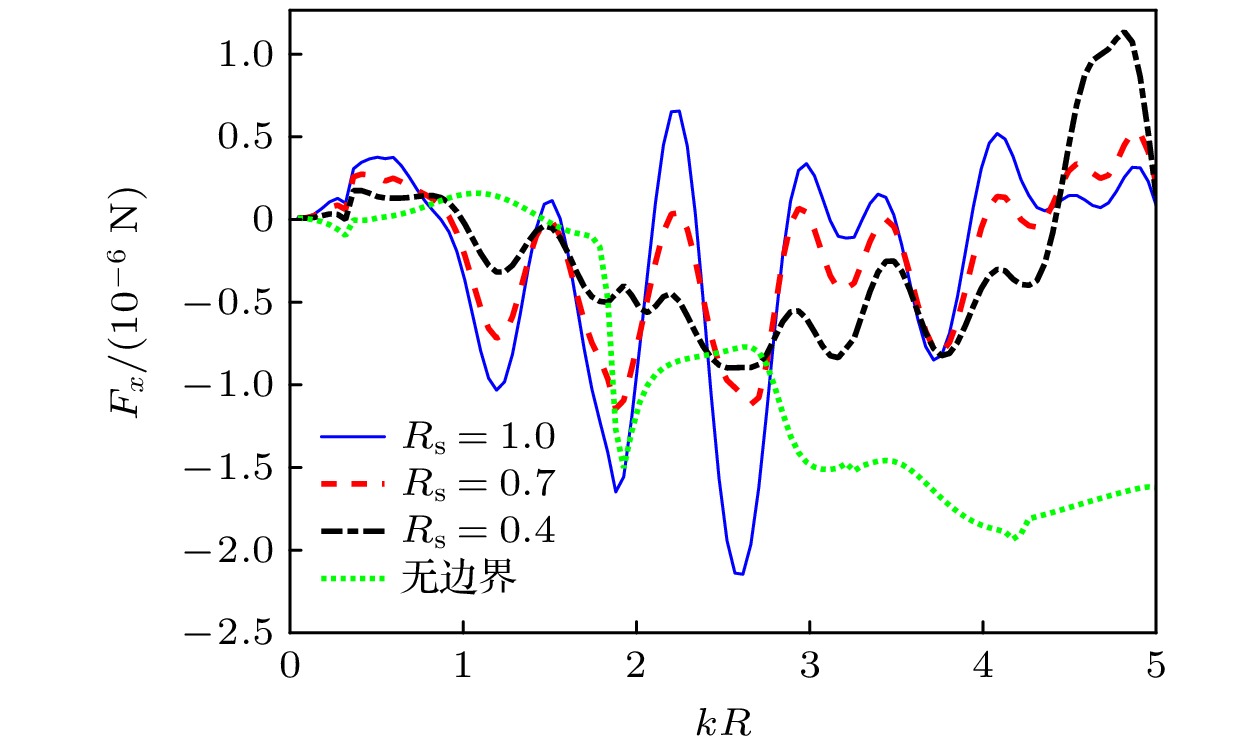
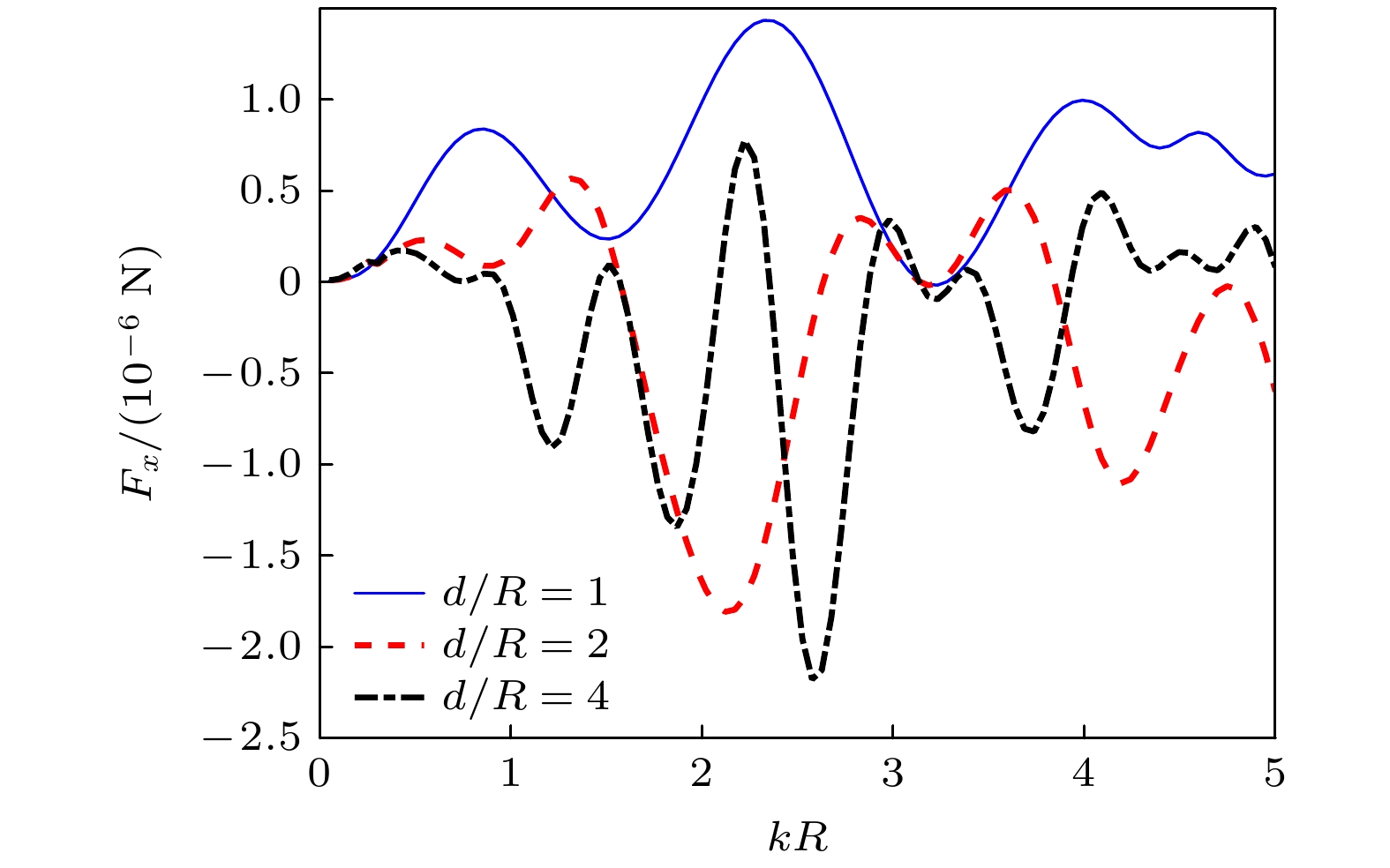
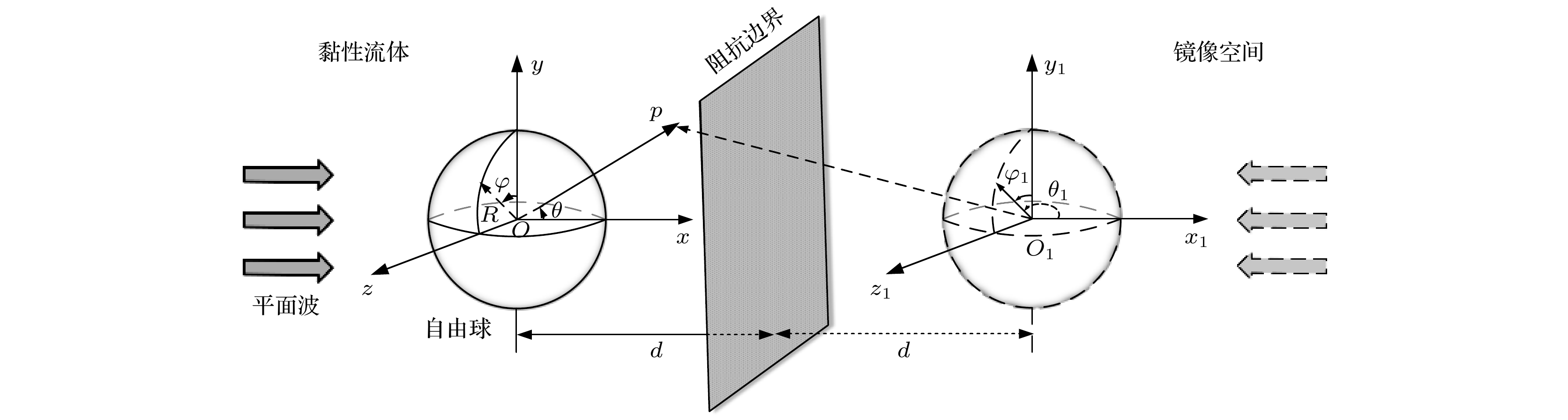
-
声辐射力的研究是提高粒子操控技术的精确性和有效性的重要基础。基于声波动理论，建立了有界粘性流体中自由球形粒子的声辐射力计算模型，结合球函数的加性定理，推导了平面波垂直入射情况下相应的声辐射力解析表达式。理论计算中考虑了小球为自由状态，将粒子的动力学方程作为计算声辐射力的修正项。在考虑流体粘度、粒子材料、粒子位置以及边界等因素对声辐射力影响的基础上进行了数值计算。结果表明,随着流体粘度的增加，声辐射力曲线的共振峰被拓宽；相比于液体材料的小球，弹性材料小球的声辐射力的振荡现象更明显；随着阻抗边界反射系数的增大，声辐射力振幅增大；小球位置的不同主要影响其声辐射力的振荡现象。该研究为有界粘性流体中自由粒子的声操控提供了理论基础，并有助于生物医学等领域更好地利用声辐射力操控粒子。The manipulation of particles by acoustic radiation force (ARF) has the advantages of non-invasiveness, high biocompatibility, and wide applicability. The study of acoustic radiation force is an important foundation for improving the accuracy and effectiveness of particle manipulation technology. Based on the acoustic wave theory, a theoretical model for the ARF of a free spherical particle in a bounded viscous fluid is established. The ARF for the case of a normal incident plane wave is derived by applying the translation addition theorem for spherical function. The dynamic equation of the free sphere is required as a correction term for calculating the ARF. The effects of the fluid viscosity, particle material, particle distance from boundary, and the boundary on the ARF are analyzed by numerical simulation. The results show that the resonance peak of the ARF curve is broadened with increase of the viscosity of the fluid. Comparing the values of the ARFs of a PE sphere in a viscous and an ideal fluid, it is found that the influence of fluid viscosity is small and the viscosity effect can be ignored when kR is much less than 1; However, for cases where kR is greater than or equal to 1, the amplitude of the ARF experienced by a particle in a viscous fluid is much greater than that in an ideal fluid. The influence of fluid viscosity on the ARF is significant and cannot be ignored. Moreover, compared to a liquid material sphere, the oscillation of ARF in an elastic material sphere is more pronounced. This is because the momentum transfer between sound waves and elastic materials is greater than that between sound waves and liquid materials. In addition, the amplitude of the ARF increases as increasing the reflection coefficient of the impedance boundary, but its resonance frequency is not affected. Finally, the position of the sphere mainly affects the oscillation phenomenon of its ARF. The peaks and dips of the ARF become more densely packed with the growth of distance-to-radius. It is worth noting that the reflection coefficient mainly affects the amplitude of the ARF, while the position of the sphere affects the period of the ARF function. The results indicate that more efficient manipulation of particles can be achieved through appropriate parameter selection. This study provides a theoretical basis for the acoustic manipulation of a free particle in a bounded viscous fluid and contributes to the better utilization of ARF for particle manipulation in biomedical and other fields.
-
[1] Ozcelik A, Rufo J, Guo F, Gu Y, Li P, Lata J, Huang T J 2018Nat. Methods 15 1021
[2] Meng L, Cai F, Li F, Zhou W, Niu L, Zheng H 2019J. Phys. D Appl. Phys. 52 273001
[3] King L V 1934proc. R. Soc. London 147 861
[4] Hasegawa T, Yosioka K 1969J. Acoust. Soc. Am. 46 5
[5] Marston P L 2006J. Acoust. Soc. Am. 120 3518
[6] Gong Z X, Marston P L, Li W 2019Phys. Rev. E 99 063004
[7] Zang Y C, Su C, Wu P F, Lin W J 2022Acta Phys. Sin. 71 10(in Chinese) [臧雨宸, 苏畅, 吴鹏飞, 林伟军2022物理学报71 10]
[8] Li S Y, Shi J Y, Zhang X F, Zhang G B 2019J. Acoust. Soc. Am. 145 5
[9] Azarpeyvand M, Azarpeyvand M 2013J. Sound Vib. 332 9
[10] Zang Y C, Lin W 2019Results Phys. 16 102847
[11] Mitri F G 2009Ultrasonics 49 794
[12] Marston P L 2009J. Acoust. Soc. Am. 125 6
[13] Gong M Y, Shi M J, Li Y Y, Xu X, Fei Z H, Qiao Y P, Liu J H, He A J, Liu X Z 2023Phys. Fluids 35 057108
[14] Gong M Y, Xu X, Qiao Y P, Liu J H, He A J, Liu X Z 2024Chinese Phys. B 33 014302.
[15] Gaunaurd G C, Huang H 1991J. Acoust. Soc. Am. 96 2526
[16] Miri A K, Mitri F G 2011Ultrasound Med. Biol. 37 2
[17] Westervelt P J 1951J. Acoust. Soc. Am. 23 3
[18] Doinikov A A 1994J. Fluid Mech 267 1
[19] Qiao Y P, Gong M Y, Wang H B, Lan J, Liu T, Liu J H, Mao Y W, He A J, Liu X Z 2021Phys. Fluids 33 047107
[20] Kundu P K, Cohen I M 2002Fluid Mechanics (San Diego: Academic Press) p78，p96
[21] Huang H, Gaunaurd G C 1997Int. J. Solids Struct. 34 591
[22] Hasheminejad S M 2001Acta Acust. United Ac. 87 4
[23] Embleton T F W 1954J. Acoust. Soc. Am. 26 1
[24] Yosioka K, Kawasima Y 1955Acta. Acust. United. Ac. 5 3
[25] Wang H B, Gao S, Qiao Y P, Liu J H, Liu X Z 2019Phys. Fluids 31 047103
[26] Hartman B, Jarzynski J 1972J. Appl. Phys. 43 11
计量
- 文章访问数: 117
- PDF下载量: 0
- 被引次数: 0
下载:
