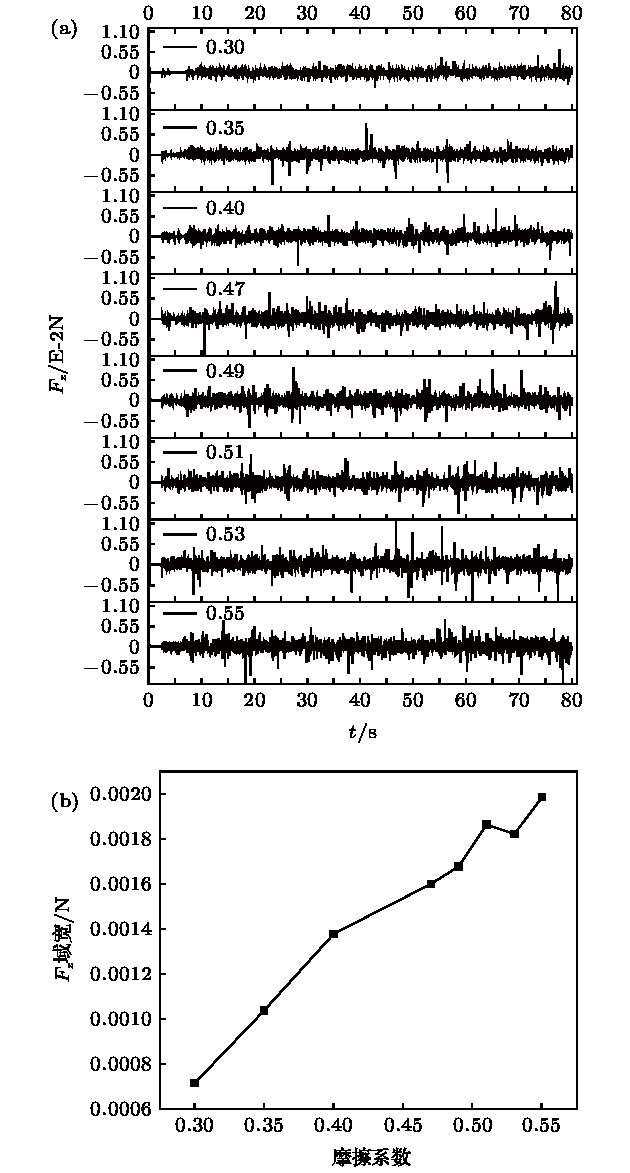
-
Particle separation is important in industrial production. The granular powder exhibits the property that is like both fluid property and solid property, which makes it difficult to establish a mathematical model to reveal the particle motion mechanism. The fluid property of the granular powder can be partly explained by the classical fluid theory, but the solid property cannot be covered. Theories combining the fluid and solid properties are also used to explain the particle separation phenomenon. However, they are not in consensus about the granular theory to explain the particle separation mechanism. Friction dissipation, which represents the particle pairwise damp interactions, greatly influences the particle separation process. In order to understand the particle separation mechanism and the effect of friction coefficient on the particle motion, a three-dimensional discrete element model is used to simulate the separation of three-dimensional spherical binary particles in a cylindrical groove （shear cell）in this paper. Initially, the large particle is placed at the bottom and the other small particles pile into the groove. The shear flow of the particles is established by rotating the bottom plate of the groove. The large particles gradually jump to the top of the groove under the shearing action. The effect of particle friction coefficient on the separation is studied. Focusing on the characteristics of kinematics and dynamics in the jumping process of large particle, the influence of the friction coefficient on the trajectory, velocity and acceleration of particle are quantitatively analyzed. The conclusions are obtained as follows. 1) The process of large particle jumping can be divided into three stages: relaxation stage (the large particle stays at the bottom of the groove), the take-off stage (the large particle rises up), and the equilibrium stage(the large particle moves to the top and stays there). 2) The relaxation time decreases with friction coefficient increasing. 3) The equilibrium height of particles increases with friction coefficient increasing. 4) The amplitude of the force pulsation of the large particle increases with friction coefficient increasing. For the behavior analysis of the ascending motion of the large particle, we propose a neighborhood analysis method and define a floating factor. The ratio of the number of small particles arranged in the upper to that in the lower adjacent space of the large particle is defined as the buoyancy factor. It is found that the buoyancy factor drops sharply at the jumping point of the large particle, forming the opportunity for the large particle jumping. It is revealed that the take-off of the large particle is the result of both the high-frequency characteristics of force fluctuation and the steep drop of buoyancy factor. The rising motion of the big particle is determined by the force and the surrounding space.
-
Keywords:
- DEM /
- shear segregation /
- particle dynamics /
- friction coefficient
[1] Jaeger H M, Nagel S R, Behringer R P 1996 Mod. Phys. 68 1259
Google Scholar
[2] Gray J M N T 2018 Annu. Rev. Fluid. Mech. 50 407
Google Scholar
[3] 陆坤权, 刘寄星 2004 物理 33 713
Google Scholar
Lu K Q, Liu J X 2004 Wuli 33 713
Google Scholar
[4] Fullmer W D, Hreny C M 2017 Annu. Rev. Fluid. Mech. 49 485
Google Scholar
[5] Ottino J M, Khakhar D V 2000 Annu. Rev. Fluid. Mech. 32 55
Google Scholar
[6] Kudrolli A 2004 Rep. Prog. Phys. 67 209
Google Scholar
[7] Schröter M, Ulrich S, Kreft J, Swift J B, Swinney H L 2006 Phys. Rev. E 74 011307
Google Scholar
[8] Liao C C 2016 Powder Technol. 288 151
Google Scholar
[9] Golick L A, Daniels K E 2009 Phys. Rev. E 80 042301
[10] May L B H, Golick L A, Phillips K C, Shearer M, Daniels K E 2009 Phys. Rev. E 81 05130
[11] Fenistein D, Martin V H 2003 Nature 425 256
Google Scholar
[12] van der Vaart K, Gajjar P, Epely-Chauvin G, Andreini N, Gray J M N T, Ancey C 2015 Phys. Rev. Lett. 114 238001
Google Scholar
[13] Guillard F, Forterre Y, Pouliquen O 2016 J. Fluid Mech. 807 R1
Google Scholar
[14] Yoon D K, Jenkins J T 2006 Phys. Fluids 17 83301
[15] Braun J 2001 Phys. Rev. E 64 011307
Google Scholar
[16] Hong D C, Quinn P V, Luding S 2001 Phys. Rev. Lett. 86 3423
Google Scholar
[17] Berzi D, Jenkins J T 2015 Phys. Fluids 27 033303
Google Scholar
[18] Liao C C, Hunt M L, Hsiau S S, Lu S H 2014 Phys. Fluids 26 073302
Google Scholar
[19] Gajjar P, Gray J M N T 2014 J. Fluid Mech. 757 297
Google Scholar
[20] Chand R, Muniandy S V, Wong C S 2017 Singh J. Particuology 32 89
Google Scholar
[21] 文平平 2016 博士学位论文 (北京: 北京理工大学)
Wen P P 2016 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[22] Ulrich S, Schroter M, Swinney H L 2007 Phys. Rev. E 76 042301
[23] Kloss C, Goniva C, Hager A, Amberger S, Priler S 2012 Comput. Fluid Dyn. 12 140
Google Scholar
[24] Zhang Y, Campbell C S 1992 J. Fluid Mech. 237 541
Google Scholar
-
图 1 三维剪切颗粒体系示意图
Figure 1. Schematic diagram of shear granular system.
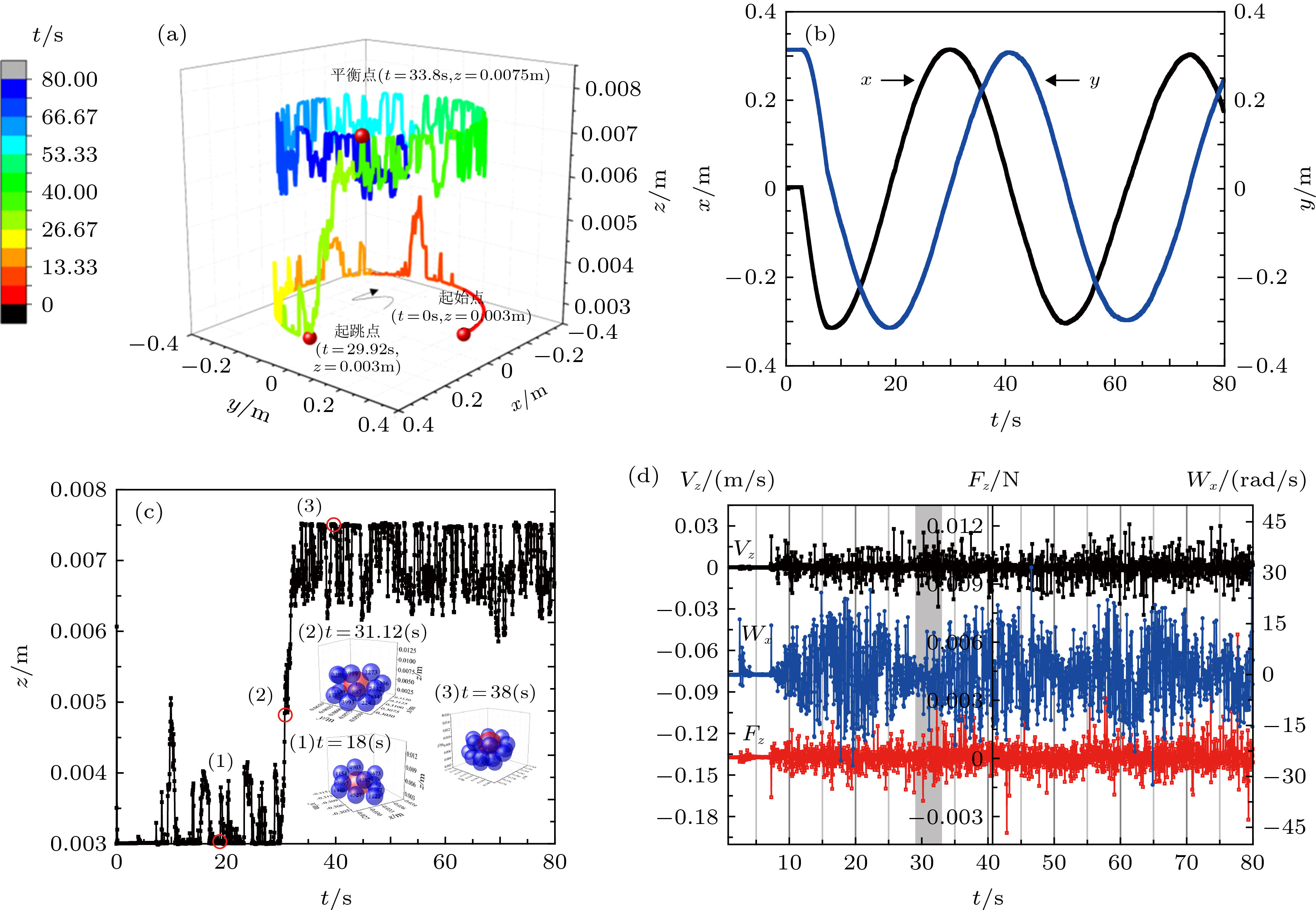
图 3 摩擦系数为0.3的大颗粒运动及力学特征图 (a)大颗粒轨迹随时间演变图; (b)大颗粒x, y方向位移随时间变化图; (c)大颗粒z方向位移随时间演变图; (d)大颗粒在z方向线速度、受力以及旋转角速度随时间变化规律, 灰色条带对应起跳过程
Figure 3. Characteristics of the large particle kinetics and kinematics with friction coefficient of 0.3: (a) Large particle trajectory evolution over time; (b) changes of large particle trajectory components in x and y directions with time; (c) changes of large particle trajectory components in z direction with time; (d) changes of translational velocity, force and rotational velocity with time.
图 4 (a)平衡高度随摩擦系数变化图; (b)起跳弛豫时间随摩擦系数变化图
Figure 4. (a) Equilibrium height versus friction coefficient; (b) relaxation time changes with friction.
图 5 (a)不同摩擦系数下z方向受力Fz时间变化序列; (b) Fz脉动域宽随摩擦系数的变化规律
Figure 5. (a) Fz changes with time for different friction coefficients; (b) Fz oscillation magnitude changes with friction coefficients.
图 6 浮升因子计算模型
Figure 6. Floating factor calculation model.
图 7 起跳过程中浮升因子随时间变化图 (a)−(c)浮升因子在颗粒起跳过程中的变化规律, 摩擦系数分别为0.35 (a) 0.49 (b) 0.55 (c) 图中彩色线表示浮升因子, 黑色实线表示对应时刻颗粒高度的变化过程; (d)随摩擦系数增大浮升因子突降转变点提前
Figure 7. The floating factor variation with time under the friction coefficients of 0.35 (a), 0.49 (b) and 0.55 (c). The color line indicates the floating factor, and the black line represents the z trajectory. (d) sharp decrease point of the floating factor occurs earlier with friction coefficient increment.
表 1 模拟参数
Table 1. Simulation parameters.
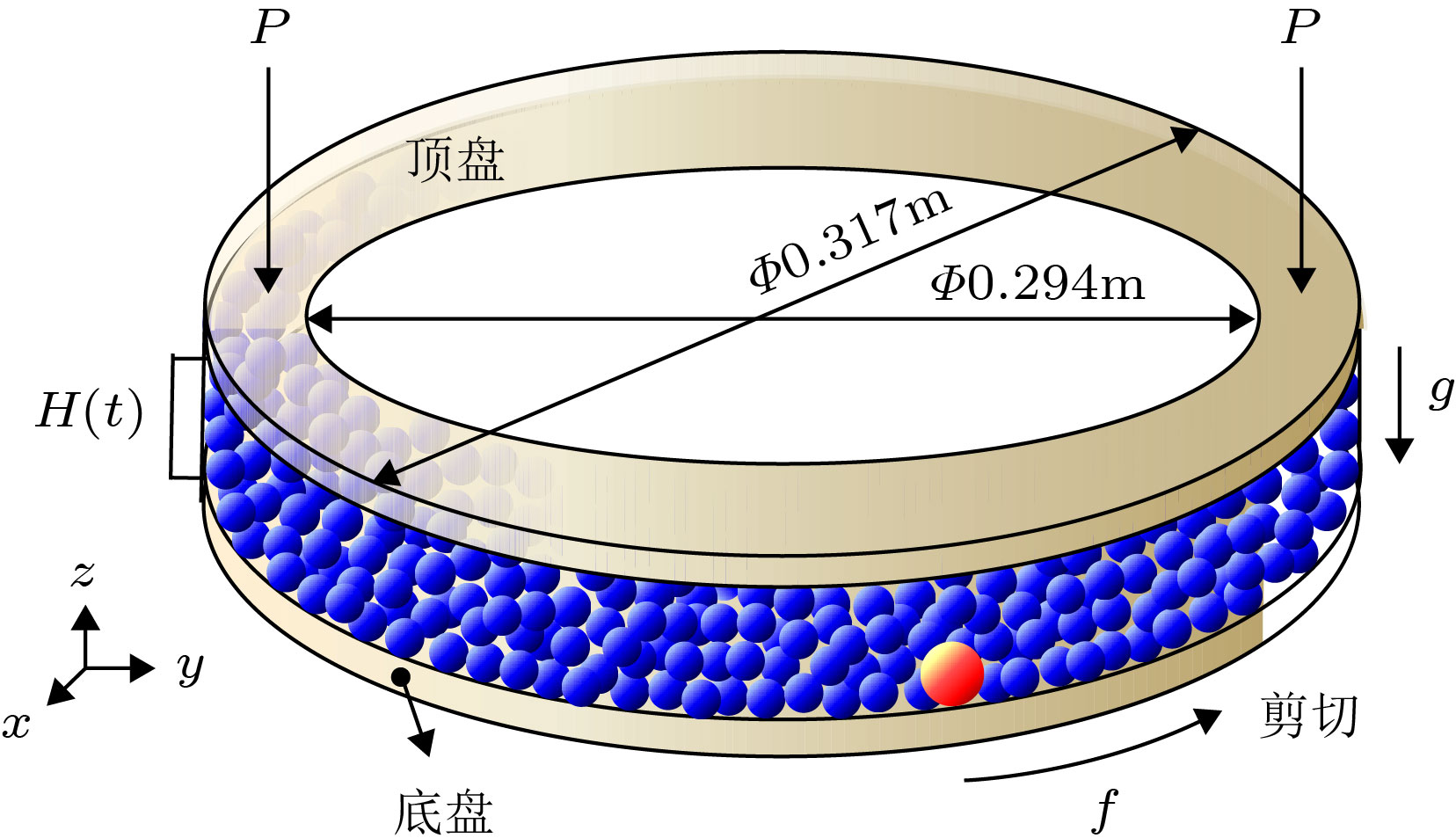
参量 数值 杨氏模量Y/Pa 107 泊松系数ν 0.25 恢复系数e 0.5 摩擦系数f 0.3, 0.35, 0.4, 0.45, 0.47, 0.49, 0.51, 0.55, 0.6 颗粒直径R/m 0.002 (小颗粒), 0.003 (大颗粒) 颗粒密度ρ/kg·m–3 1000 时间步长t/s 2 × 10–6 模拟物理时间t/s 80 
DownLoad: CSV
-
[1] Jaeger H M, Nagel S R, Behringer R P 1996 Mod. Phys. 68 1259
Google Scholar
[2] Gray J M N T 2018 Annu. Rev. Fluid. Mech. 50 407
Google Scholar
[3] 陆坤权, 刘寄星 2004 物理 33 713
Google Scholar
Lu K Q, Liu J X 2004 Wuli 33 713
Google Scholar
[4] Fullmer W D, Hreny C M 2017 Annu. Rev. Fluid. Mech. 49 485
Google Scholar
[5] Ottino J M, Khakhar D V 2000 Annu. Rev. Fluid. Mech. 32 55
Google Scholar
[6] Kudrolli A 2004 Rep. Prog. Phys. 67 209
Google Scholar
[7] Schröter M, Ulrich S, Kreft J, Swift J B, Swinney H L 2006 Phys. Rev. E 74 011307
Google Scholar
[8] Liao C C 2016 Powder Technol. 288 151
Google Scholar
[9] Golick L A, Daniels K E 2009 Phys. Rev. E 80 042301
[10] May L B H, Golick L A, Phillips K C, Shearer M, Daniels K E 2009 Phys. Rev. E 81 05130
[11] Fenistein D, Martin V H 2003 Nature 425 256
Google Scholar
[12] van der Vaart K, Gajjar P, Epely-Chauvin G, Andreini N, Gray J M N T, Ancey C 2015 Phys. Rev. Lett. 114 238001
Google Scholar
[13] Guillard F, Forterre Y, Pouliquen O 2016 J. Fluid Mech. 807 R1
Google Scholar
[14] Yoon D K, Jenkins J T 2006 Phys. Fluids 17 83301
[15] Braun J 2001 Phys. Rev. E 64 011307
Google Scholar
[16] Hong D C, Quinn P V, Luding S 2001 Phys. Rev. Lett. 86 3423
Google Scholar
[17] Berzi D, Jenkins J T 2015 Phys. Fluids 27 033303
Google Scholar
[18] Liao C C, Hunt M L, Hsiau S S, Lu S H 2014 Phys. Fluids 26 073302
Google Scholar
[19] Gajjar P, Gray J M N T 2014 J. Fluid Mech. 757 297
Google Scholar
[20] Chand R, Muniandy S V, Wong C S 2017 Singh J. Particuology 32 89
Google Scholar
[21] 文平平 2016 博士学位论文 (北京: 北京理工大学)
Wen P P 2016 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[22] Ulrich S, Schroter M, Swinney H L 2007 Phys. Rev. E 76 042301
[23] Kloss C, Goniva C, Hager A, Amberger S, Priler S 2012 Comput. Fluid Dyn. 12 140
Google Scholar
[24] Zhang Y, Campbell C S 1992 J. Fluid Mech. 237 541
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7771
- PDF Downloads: 47
- Cited By: 0
