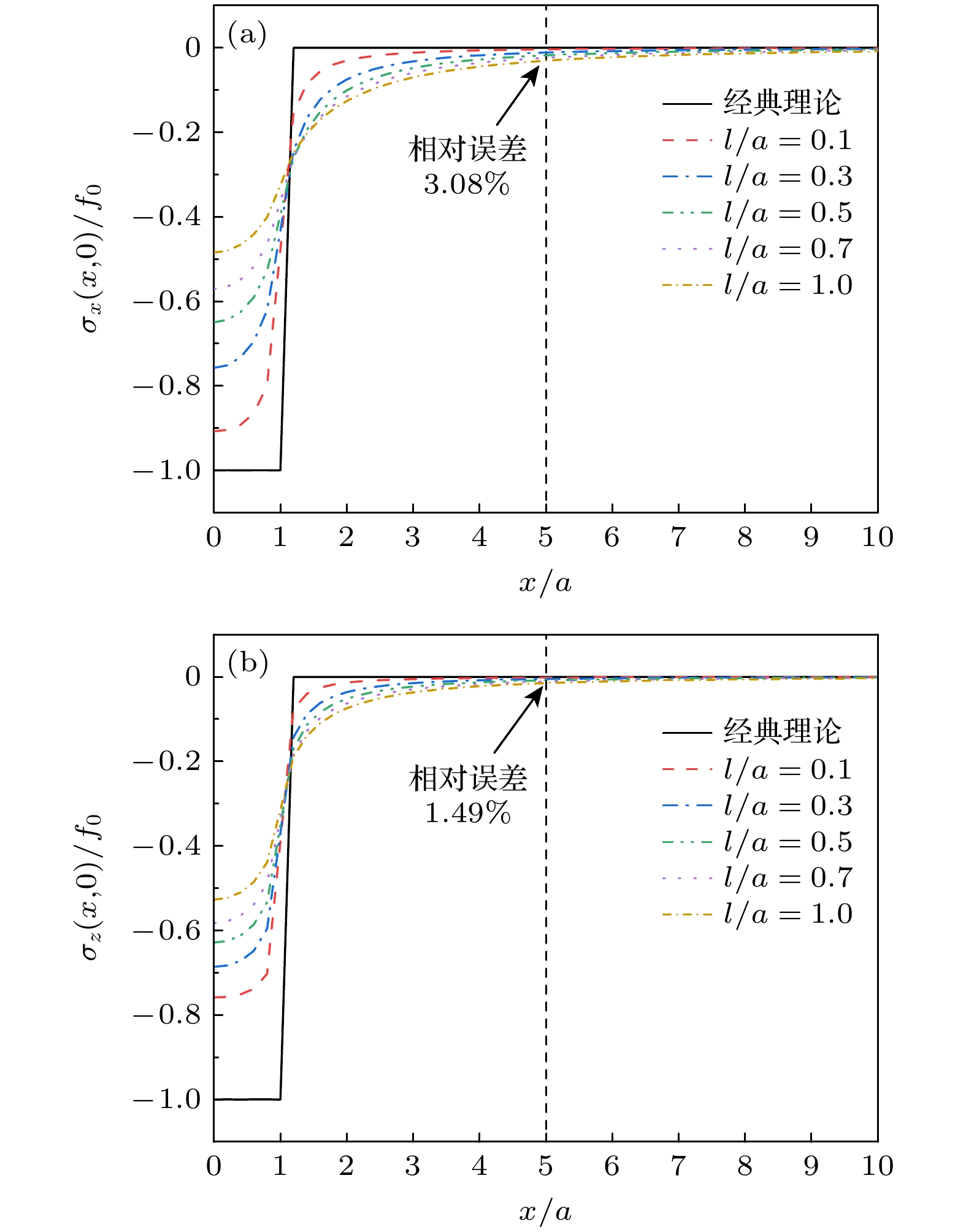
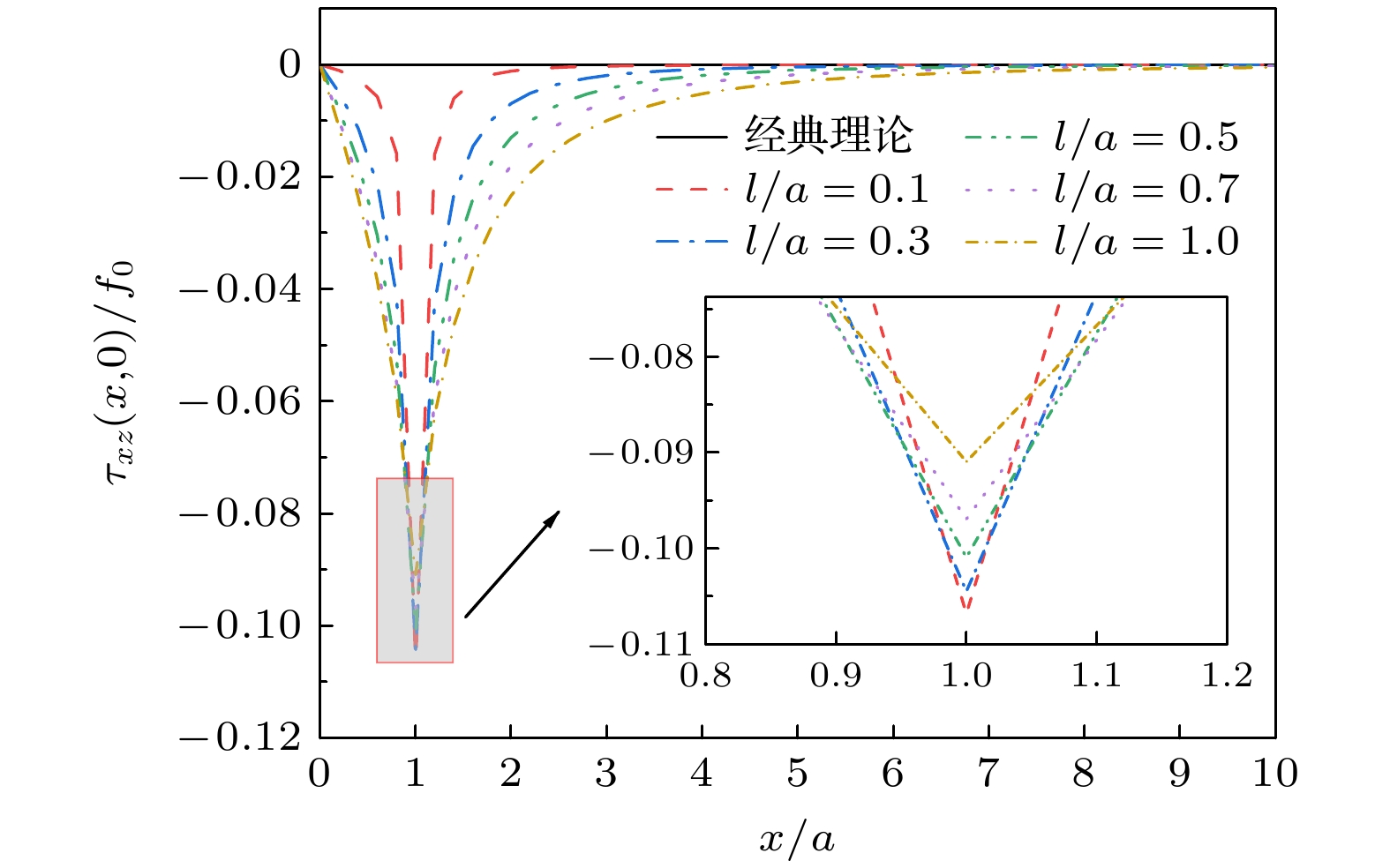
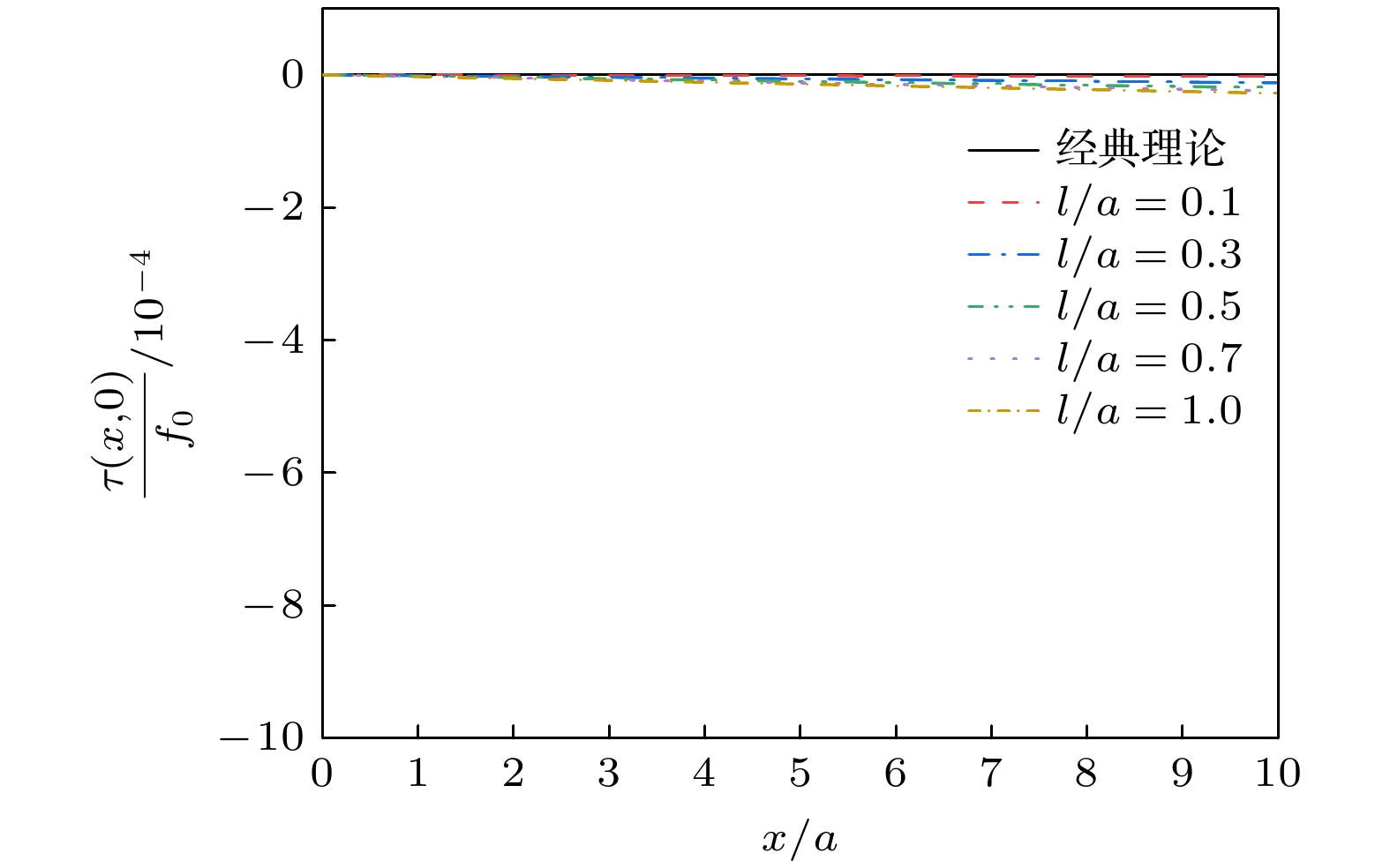
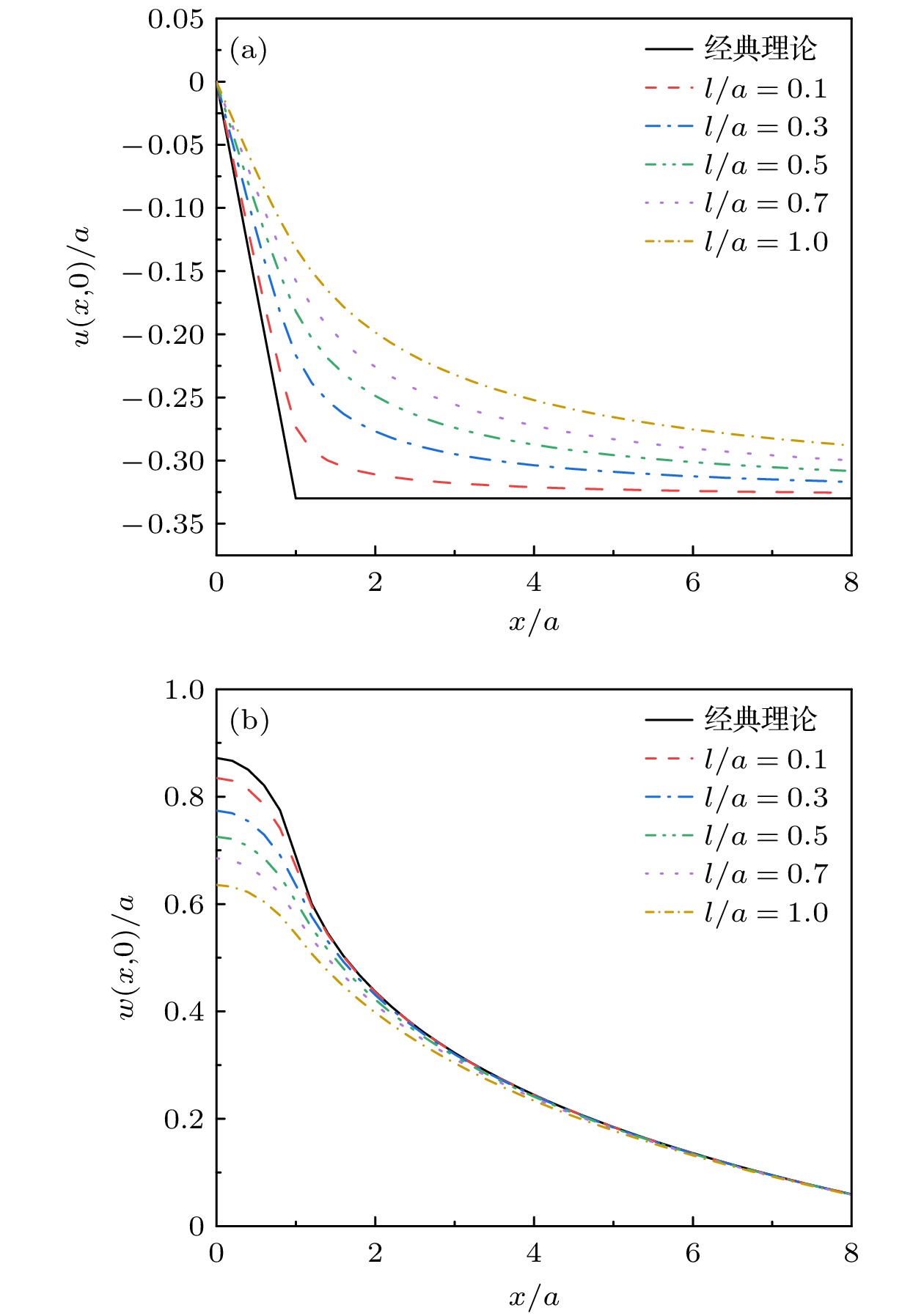
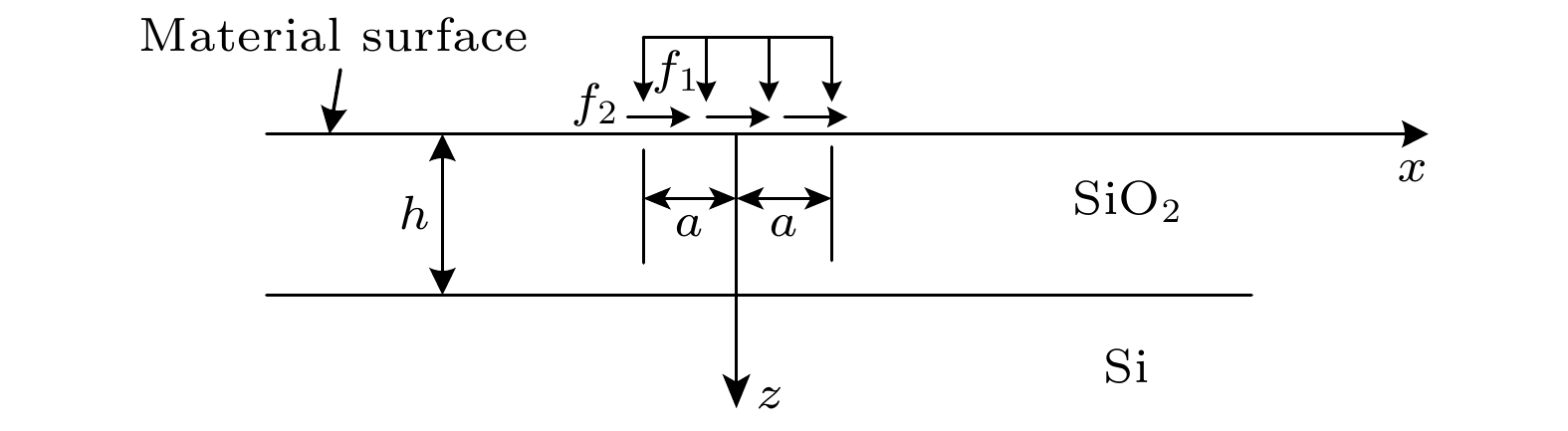
The rapid advancement of micro-nano acoustic devices has led their core acoustic structures to shrink to the nanoscale level. The influence of surface effects on the mechanical properties of thin-film materials on a nanoscale becomes increasingly prominent, and the classical elasticity theory struggles to accurately describe their mechanical behavior on this scale. In this paper, a mechanical model of nano-SiO₂/Si heterostructured thin films that considers surface effects is developed using surface elasticity theory. This model incorporates the key parameter of surface energy density. In this paper, a mechanical model of heterostructured nano-SiO₂/Si films is developed using the surface elasticity theory, incorporating surface effects through the introduction of surface energy density as a key parameter . Using the Fourier integral transform method, analytical expressions for stress and displacement fields under surface traction are systematically derived, revealing the influence of surface effects on the mechanical behavior of materials on a nanoscale by comparing the analytical solution with that from the classical theory. The results show that when the surface stress distribution deviates by 3% from that predicted by the classical theory, the microscopic properties of the material become significant, and the surface effect cannot be ignored in a range of five times the width of the excitation region 2a. As the size of the excitation region decreases, the surface effect is significantly increases and the stress distribution within the excitation region and near the boundary becomes more concentrated than the counterparts in the classical theory. The shear stress is no longer zero, and an extreme value is observed at the boundary, which is significantly different from that predicted by the classical theory of elasticity. The transverse and longitudinal displacements are reduced compared with those from the classical theory, and the surface stiffness and deformation resistance of the material are greatly enhanced. Significant surface effects occur on nano-heterostructure thin films, leading to large deviations in stress and displacement distributions from the results of elasticity theory. Therefore, the classical elasticity assumptions are no longer applicable in the corresponding nanoscale range. The results demonstrate that the propagation of ultrahigh-frequency nano- length acoustic waves in nanoscale solid film surfaces is significantly affected by the scale effect. The failure of the classical elastic wave theory on a nanoscale is of great value for the study of nanoscale acoustic theory. Furthermore, these findings provide a theoretical basis for the subsequent development of more precise models of interfacial effects and a more detailed investigation of the influence of the film-substrate modulus ratio.