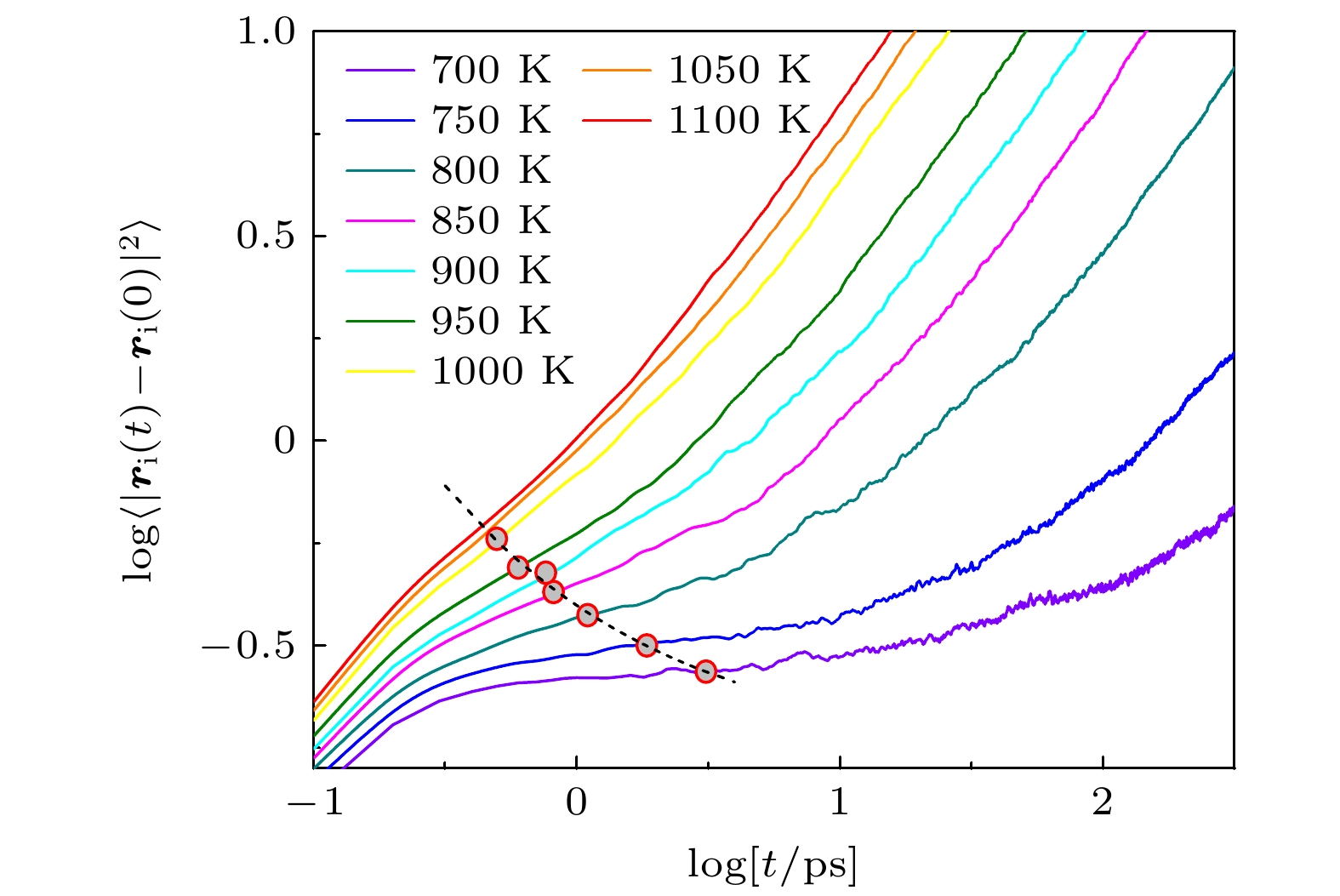
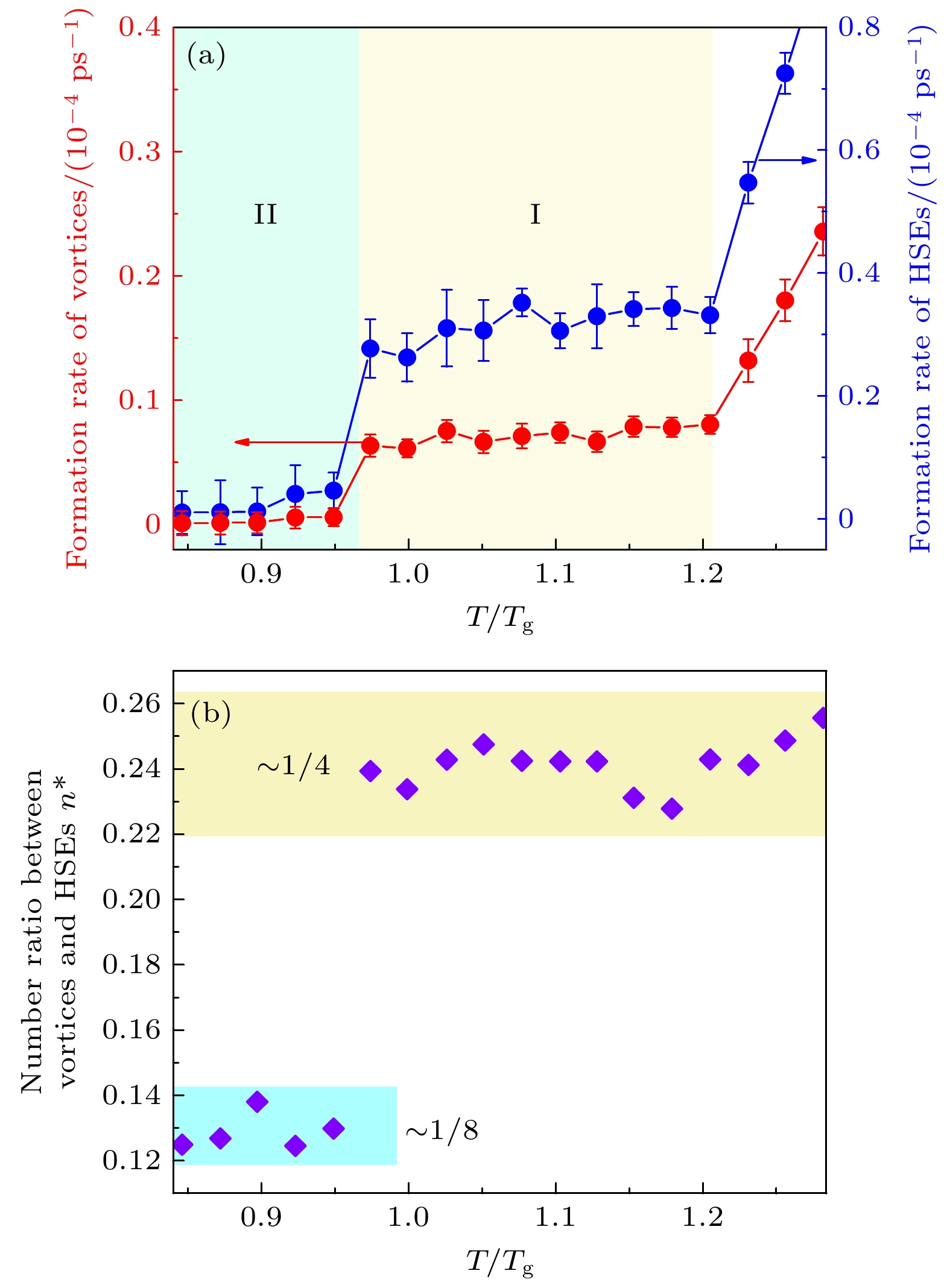
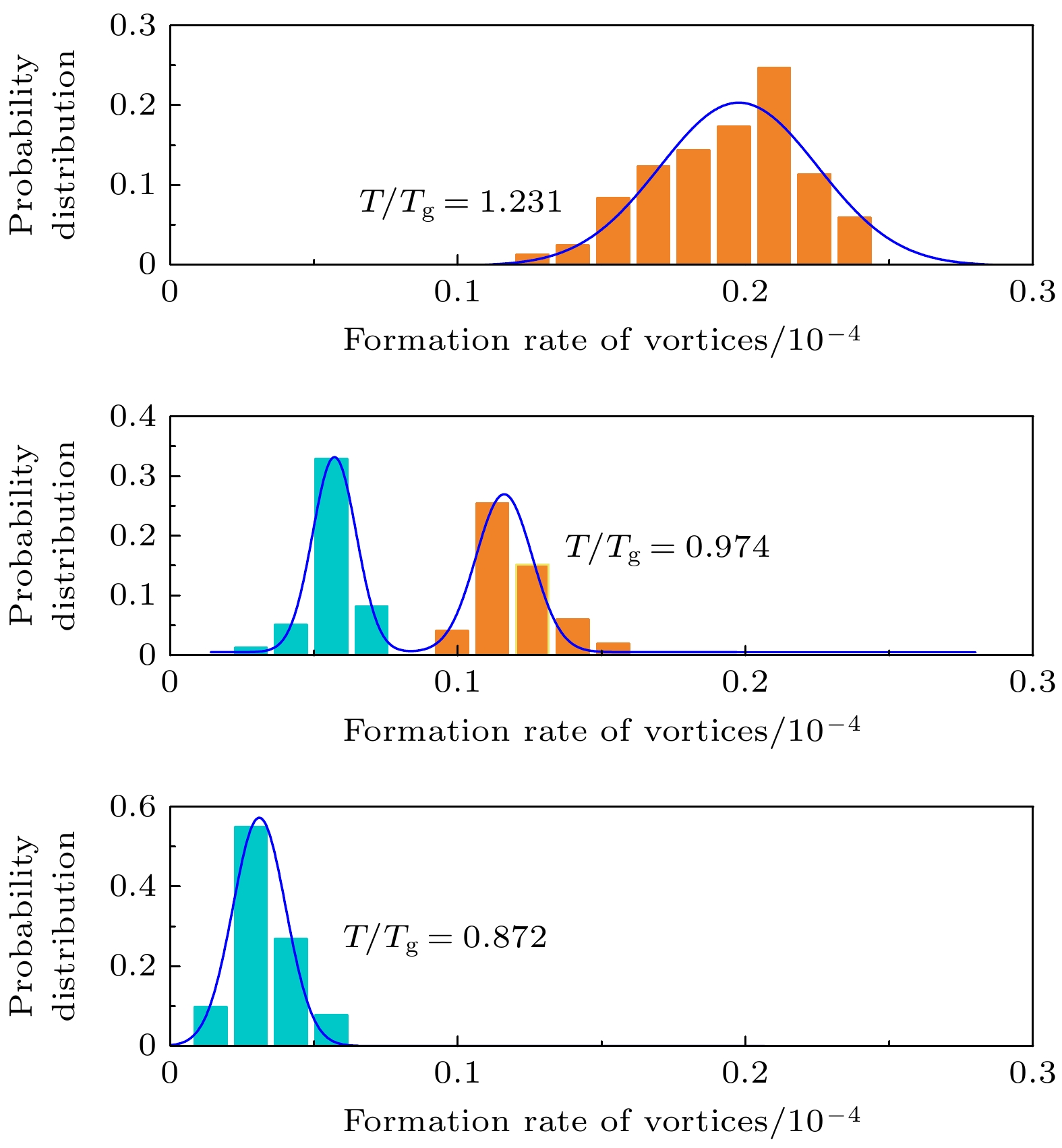
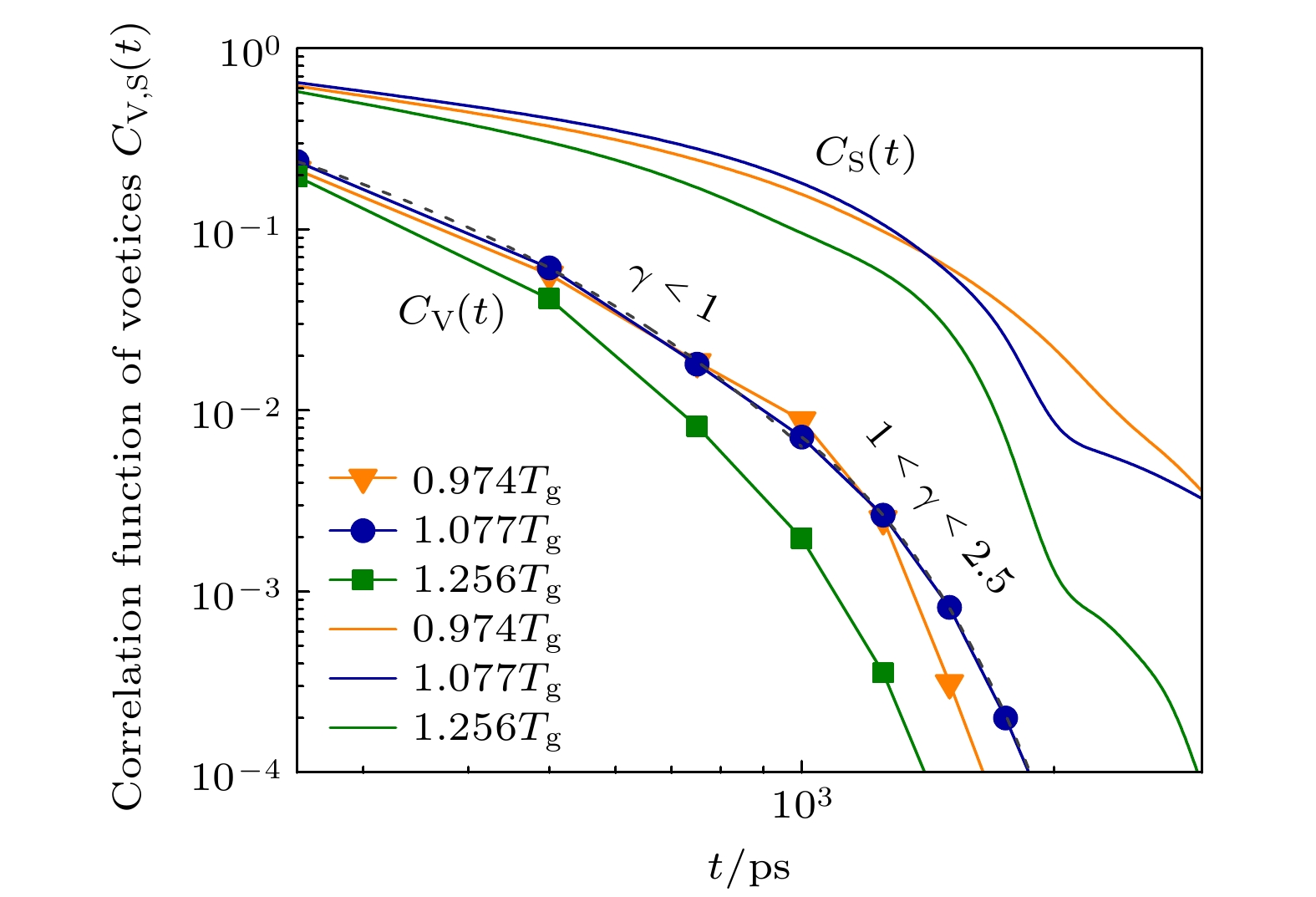
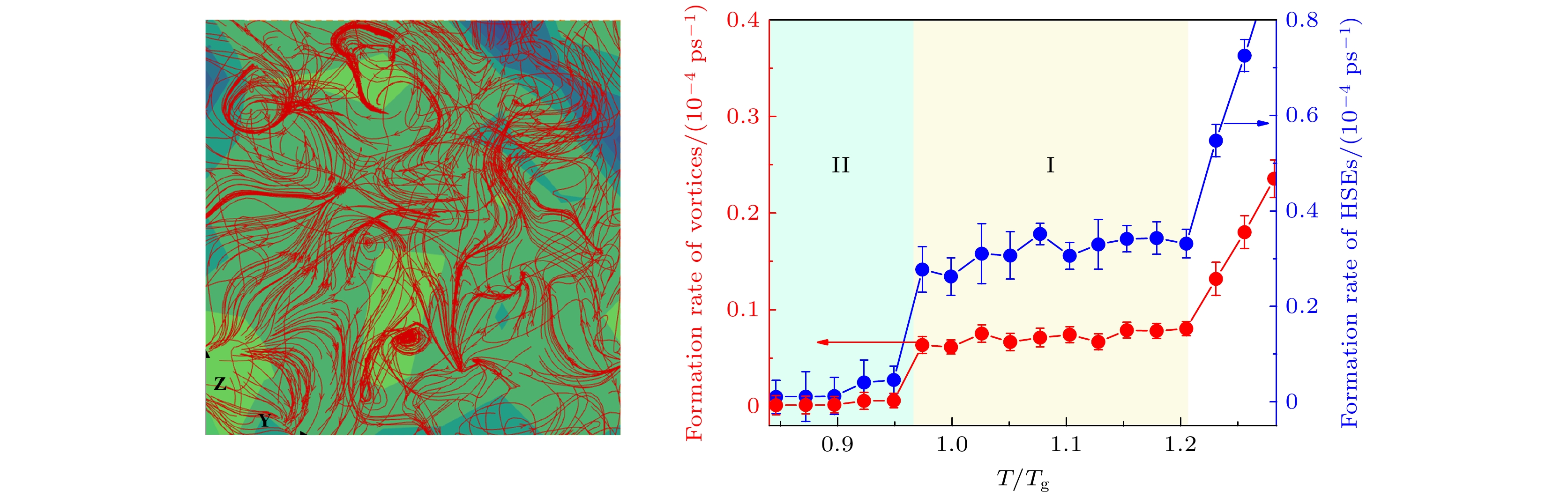
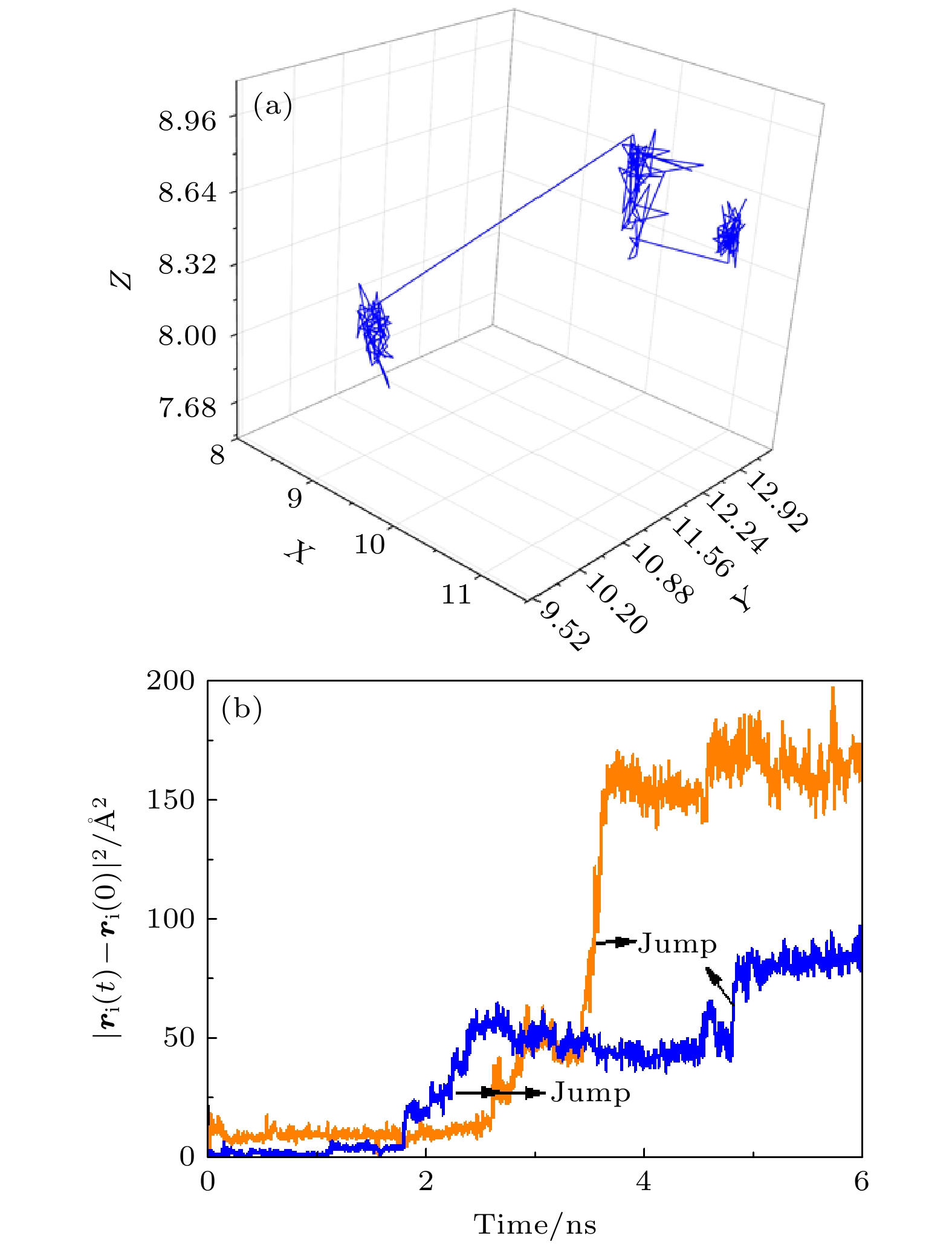
-
Metallic glass-forming systems exhibit complex dynamic behaviors during the glass transition. Understanding the dynamic nature of metallic glasses and supercooled liquids is a crucial issue in the study of glassy physics. Topological order provides a novel perspective for re-examining the dynamics of glassy systems and elucidating the physical essence of the glassy state and glass transition. In this study, the microscopic dynamics of CuZr melts in the glass transition are investigated using molecular dynamics simulations. The single-particle dynamic characteristics in the supercooled CuZr melt are the random jump motions of atoms after a long-term caging period. To capture these dynamics, the displacement vector field is constructed based on the spatiotemporal distribution of these jump events. The simulation results reveal that there exist the numerous vortex structures in the displacement vector field. Notably, the vortex formation rate, which is defined as the number of vortices generated per unit time, exhibits a sharp drop near the glass transition temperature. The probability distribution of vortex formation rate displays a bimodal pattern on the drops, indicating the coexistence of two different dynamical states related to vortex formation. Multiple high-strain events are observed surrounding these vortices. It is found that the two vortex states during the transition exhibit markedly different characteristic ratios of vortices to high-strain events (1∶4 vs 1∶8), indicating a change in the coupling strength between vortex formation and high-strain activity. The high-strain events predominantly form in the regions between positive and negative vortices, and the specific quantitative relationship between vortices and high-strain events indirectly reflects the presence of strongly interacting vortex-antivortex pairs in the melt. During the vortex state transition, the vortex-to-high-strain-event ratio suddenly doubles, which means that this transition is not only a sudden change in the rate of vortex formation, but also an enhancement of the interactions between vortex-antivortex pairs, representing a change in global topological properties. These findings demonstrate that the vortex transition exhibits the characteristics of a topological phase transition, thereby predicting the existence of a topological phase transition in the displacement vector field of metallic glass-forming systems. Further speculation suggests that vortices and high-strain events are related to multiple secondary relaxation processes. This study provides a new perspective for understanding the dynamics of glass-forming systems and the glass transition.
-
Keywords:
- topological phase transition /
- metallic glass /
- vortex /
- displacement vector field
[1] Klement W, Willens R, Duwez P 1960 Nature 187 869
Google Scholar
[2] Bernal J D 1959 Nature 183 141
Google Scholar
[3] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
Google Scholar
[4] Finney J L 1970 Proc. Roy. Soc. Lond. A 319 479
Google Scholar
[5] Miracle D B 2004 Nat. Mater. 3 697
Google Scholar
[6] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
Google Scholar
[7] Frank F C 1952 Proc. R. Soc. Lond. A 215 43
Google Scholar
[8] Hirata A, Kang L J, Fujita T, Klumov B, Matsue K, Kotani M, Yavari A R, Chen M W 2013 Science 341 376
Google Scholar
[9] 李茂枝 2017 物理学报 66 176107
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
Google Scholar
[10] 蒋元祺, 彭平 2018 物理学报 67 132101
Google Scholar
Jiang Y Q, Peng P 2018 Acta Phys. Sin. 67 132101
Google Scholar
[11] Wu C, Huang Y J, Shen J 2013 Chin. Phys. Lett. 30 106102
Google Scholar
[12] Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501
Google Scholar
[13] Lü Y J, Entel P 2011 Phys. Rev. B 84 104203
Google Scholar
[14] Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6053
Google Scholar
[15] Neophytou A, Chakrabarti D, Sciortino F 2022 Nat. Phys. 18 1248
Google Scholar
[16] Berezinskii V L 1971 Sov. Phys. JETP 32 493
[17] Kosterlitz J M, Thouless D J 1973 J. Phys. C: Solid State Phys. 6 1181
Google Scholar
[18] Kosterlitz J M 2016 Rep. Prog. Phys. 79 026001
Google Scholar
[19] DiDonna B A, Lubensky T C 2005 Phys. Rev. E 72 066619
Google Scholar
[20] Del Gado E, Ilg P, Kroeger M, Oettinger H C 2008 Phys. Rev. Lett. 101 095501
Google Scholar
[21] Dasgupta R, Hentschel H G E, Procaccia I 2012 Phys. Rev. Lett. 109 255502
Google Scholar
[22] Wu Z W, Chen Y, Wang W H, Kob W, Xu L 2023 Nature Commun. 14 2955
Google Scholar
[23] Lü Y J, Guo C C, Huang H S, Gao J A, Qin H R, Wang W H 2021 Acta Mater. 211 116873
Google Scholar
[24] Lü Y J, Qin H R, Guo C C 2021 Phys. Rev. B 104 224103
Google Scholar
[25] Tang M B, Zhao D Q, Pan M X, Wang W H 2004 Chin. Phys. Lett. 21 901
Google Scholar
[26] Mendelev M I, Kramer M J, Ott R T, Sordelet D J, Yagodin D, Popel P 2009 Philos. Mag. 89 967
Google Scholar
[27] Nosé S 1984 J. Chem. Phys. 81 511
Google Scholar
[28] Hoover W G 1985 Phys. Rev. A 31 1695
Google Scholar
[29] Plimpton S 1995 J. Comp. Phys. 117 1
Google Scholar
[30] Chou C F, Jin A J, Hui S W, Huang C C, Ho J T 1998 Science 280 1424
Google Scholar
[31] Mirkovic J, Savel’ev S E, Sugahara E, Kadowaki K 2001 Phys. Rev. Lett. 86 886
Google Scholar
[32] Kim S, Hu C R, Andrews M J 2004 Phys. Rev. B 69 094521
Google Scholar
-
图 1 CuZr合金熔体中原子“跳跃”运动图 (a)一个原子连续两次“跳跃”的轨迹图; (b) “跳跃”运动所对应的平方位移曲线, 橙色和蓝色表示不同的两个粒子
Figure 1. Jump motion of atoms in CuZr melt: (a) Spatial trajectory of successive jumps; (b) a time-res squared displacement of jumping atoms, orange and blue represent two different types of particles.
图 2 不同温度下CuZr合金熔体的均方位移与时间的对数图, 圆圈表示曲线的拐点, 虚线表示对各个温度下拐点的指数拟合
Figure 2. Logarithm plot of mean squared displacements at various temperatures in CuZr melt, the open circles denote the inflection points in curves and the dashed line is an exponential-function fit to the inflection points.
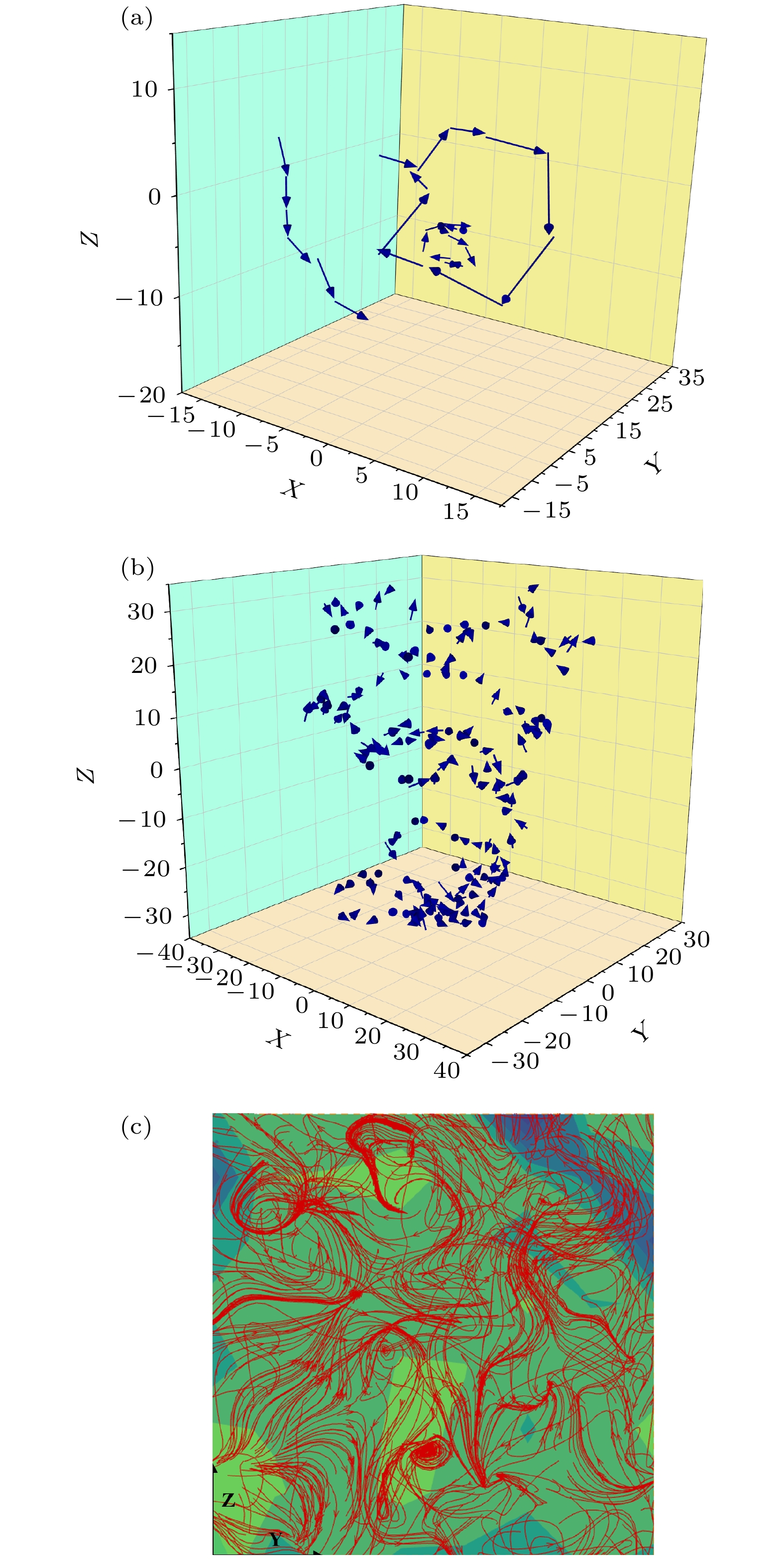
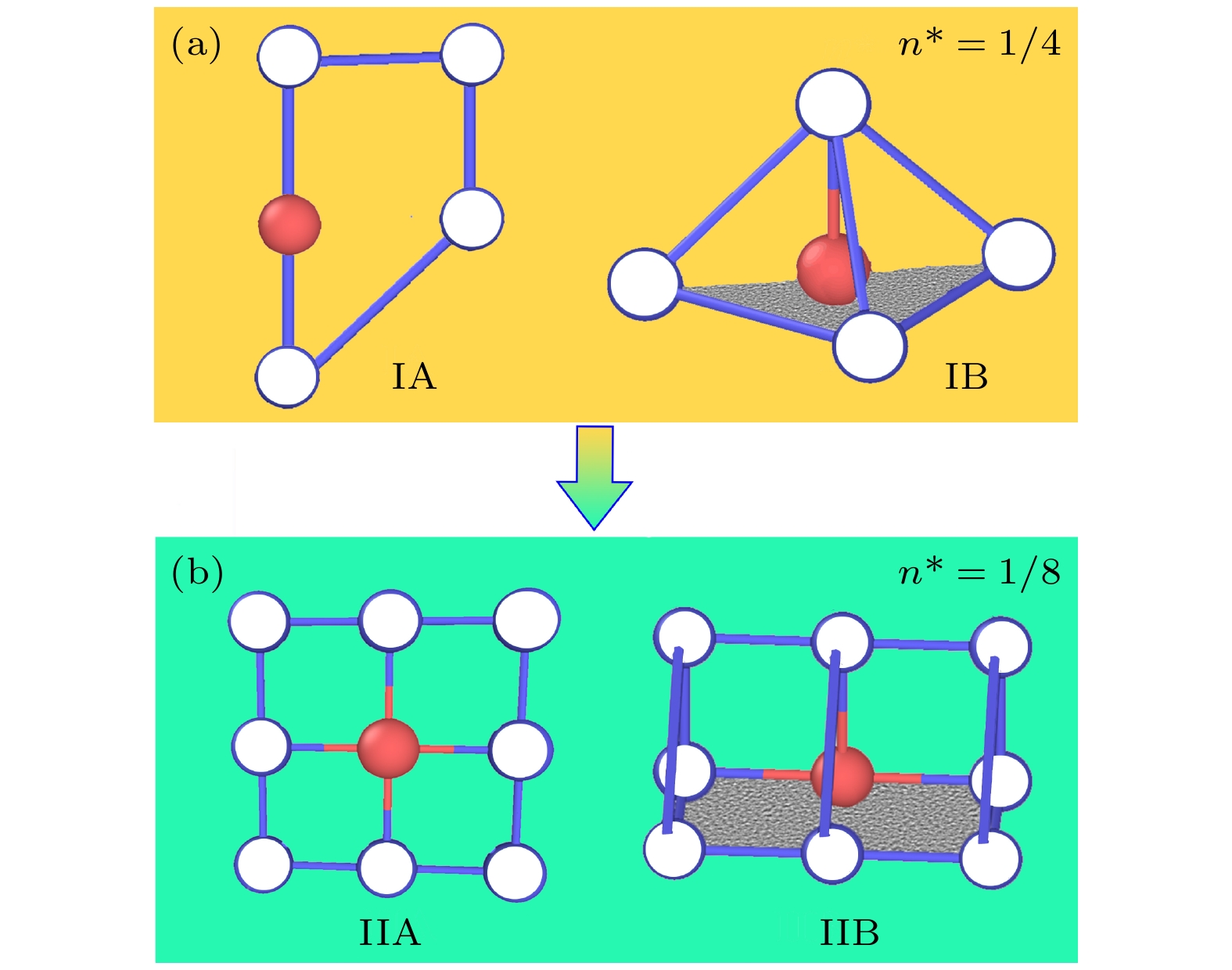
图 3 CuZr过冷合金熔体中原子“跳跃”运动的空间构型 (a)在较短的观察时间内观察到弦链状或环状结构; (b)在较长观察时间内观察到的涡旋结构; (c)位移矢量流场在X方向上的一个剖面, 可以观察到由大量涡旋构成的涡旋阵列
Figure 3. Spatial configuration of jump motions of atoms in supercooled CuZr melt: (a) String- and loop-like configurations observed in a short time interval; (b) vortex that is observed in a relatively long time; (c) a cross section of the flow field of atomic displacements along the X direction, which shows a disordered vortex lattice composed of vortices.
图 4 涡旋和高应变事件形成率 (a)涡旋和高应变事件形成率随约化温度的变化; (b)涡旋数与高应变事件形成率之比随约化温度的变化
Figure 4. Formation rates of vortices and HSEs: (a) Formation rates of vortices and HSEs versus scaled temperature; (b) ratio of vortex to HSE formation rates as a function of scaled temperature.
图 5 涡旋态转变过程中, 在T/Tg = 1.231, 0.974和0.872三个温度下系统涡旋形成率的概率分布
Figure 5. Probability distributions of vortex formation rates at T/Tg = 1.231, 0.974和0.872, which spans the vortex transition.
图 6 涡旋和高应变事件结构示意图 (a) 涡旋态I的两种结构; (b)涡旋态II的两种结构. 圆圈表示涡旋周边的高应变事件
Figure 6. Schematic diagram of vortex and high-strain event pairs. Two configurations of the vortex state I (a) and II (b). The open circles denote the high strain events surrounding a vortex.
图 7 不同温度下涡旋(符号)和高应变事件(实线)的自相关函数. 虚线表示用不同指数的KWW函数拟合短时和长时关联函数
Figure 7. Autocorrelation functions of vortices (symbols) and high strain events (solid lines) at different temperatures. The dashed lines represent the KWW fits with different exponents to the short- and long-time decays of vortices.
-
[1] Klement W, Willens R, Duwez P 1960 Nature 187 869
Google Scholar
[2] Bernal J D 1959 Nature 183 141
Google Scholar
[3] Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379
Google Scholar
[4] Finney J L 1970 Proc. Roy. Soc. Lond. A 319 479
Google Scholar
[5] Miracle D B 2004 Nat. Mater. 3 697
Google Scholar
[6] Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419
Google Scholar
[7] Frank F C 1952 Proc. R. Soc. Lond. A 215 43
Google Scholar
[8] Hirata A, Kang L J, Fujita T, Klumov B, Matsue K, Kotani M, Yavari A R, Chen M W 2013 Science 341 376
Google Scholar
[9] 李茂枝 2017 物理学报 66 176107
Google Scholar
Li M Z 2017 Acta Phys. Sin. 66 176107
Google Scholar
[10] 蒋元祺, 彭平 2018 物理学报 67 132101
Google Scholar
Jiang Y Q, Peng P 2018 Acta Phys. Sin. 67 132101
Google Scholar
[11] Wu C, Huang Y J, Shen J 2013 Chin. Phys. Lett. 30 106102
Google Scholar
[12] Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501
Google Scholar
[13] Lü Y J, Entel P 2011 Phys. Rev. B 84 104203
Google Scholar
[14] Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6053
Google Scholar
[15] Neophytou A, Chakrabarti D, Sciortino F 2022 Nat. Phys. 18 1248
Google Scholar
[16] Berezinskii V L 1971 Sov. Phys. JETP 32 493
[17] Kosterlitz J M, Thouless D J 1973 J. Phys. C: Solid State Phys. 6 1181
Google Scholar
[18] Kosterlitz J M 2016 Rep. Prog. Phys. 79 026001
Google Scholar
[19] DiDonna B A, Lubensky T C 2005 Phys. Rev. E 72 066619
Google Scholar
[20] Del Gado E, Ilg P, Kroeger M, Oettinger H C 2008 Phys. Rev. Lett. 101 095501
Google Scholar
[21] Dasgupta R, Hentschel H G E, Procaccia I 2012 Phys. Rev. Lett. 109 255502
Google Scholar
[22] Wu Z W, Chen Y, Wang W H, Kob W, Xu L 2023 Nature Commun. 14 2955
Google Scholar
[23] Lü Y J, Guo C C, Huang H S, Gao J A, Qin H R, Wang W H 2021 Acta Mater. 211 116873
Google Scholar
[24] Lü Y J, Qin H R, Guo C C 2021 Phys. Rev. B 104 224103
Google Scholar
[25] Tang M B, Zhao D Q, Pan M X, Wang W H 2004 Chin. Phys. Lett. 21 901
Google Scholar
[26] Mendelev M I, Kramer M J, Ott R T, Sordelet D J, Yagodin D, Popel P 2009 Philos. Mag. 89 967
Google Scholar
[27] Nosé S 1984 J. Chem. Phys. 81 511
Google Scholar
[28] Hoover W G 1985 Phys. Rev. A 31 1695
Google Scholar
[29] Plimpton S 1995 J. Comp. Phys. 117 1
Google Scholar
[30] Chou C F, Jin A J, Hui S W, Huang C C, Ho J T 1998 Science 280 1424
Google Scholar
[31] Mirkovic J, Savel’ev S E, Sugahara E, Kadowaki K 2001 Phys. Rev. Lett. 86 886
Google Scholar
[32] Kim S, Hu C R, Andrews M J 2004 Phys. Rev. B 69 094521
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 429
- PDF Downloads: 13
- Cited By: 0
