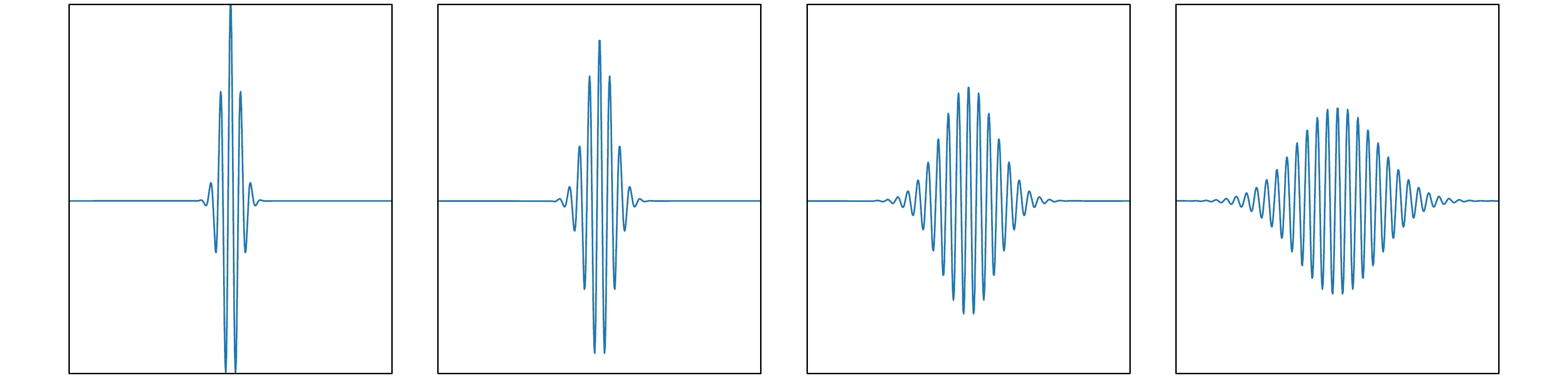
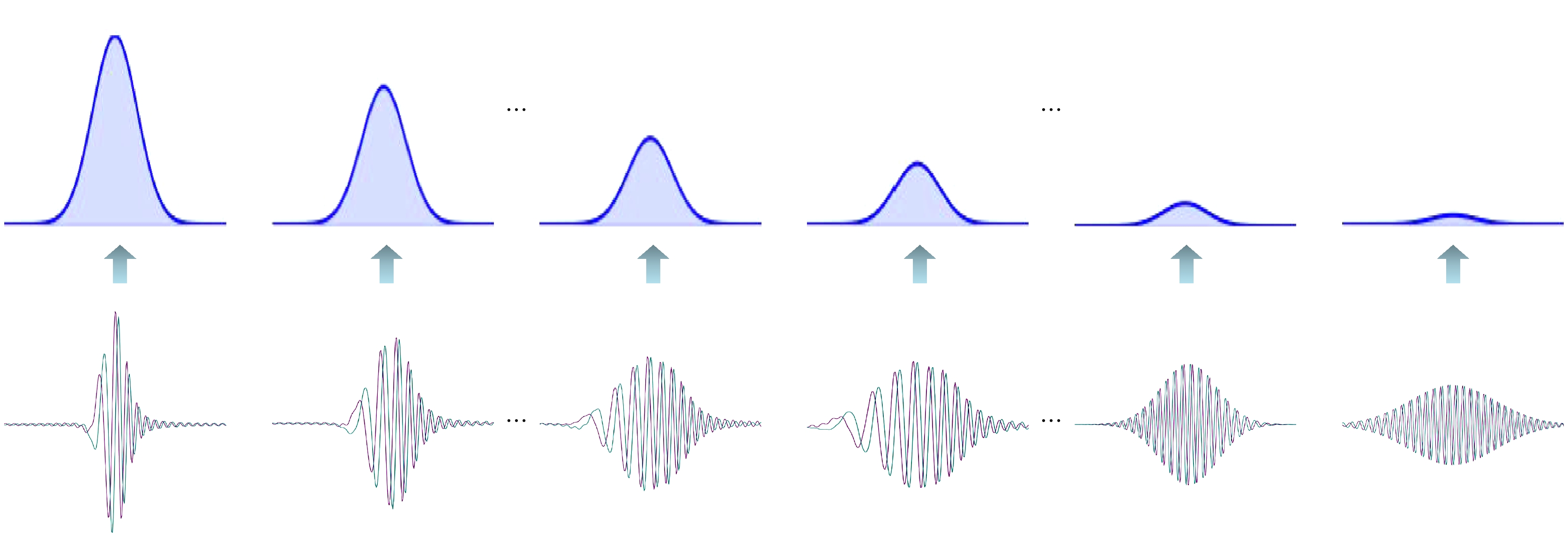
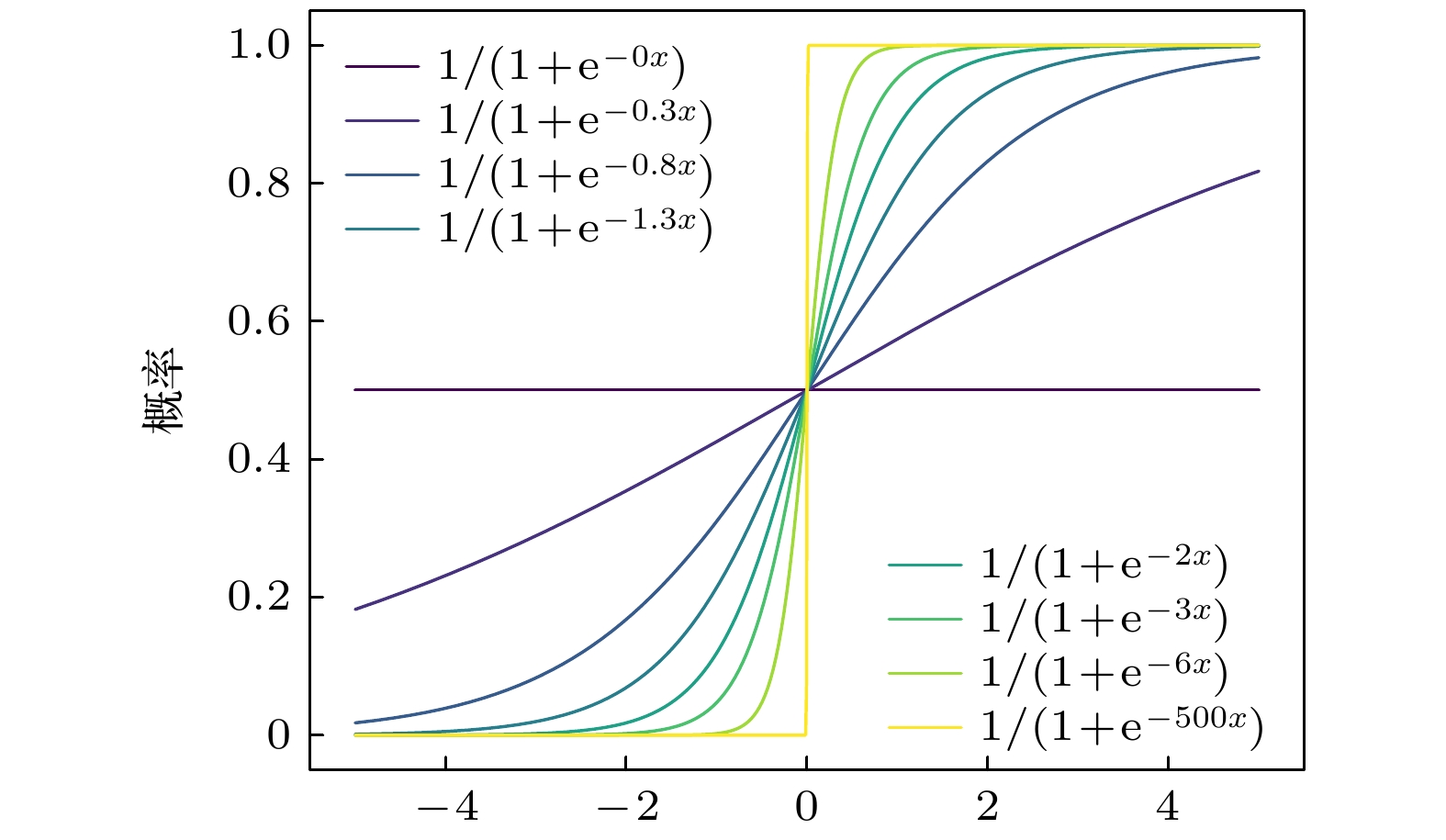
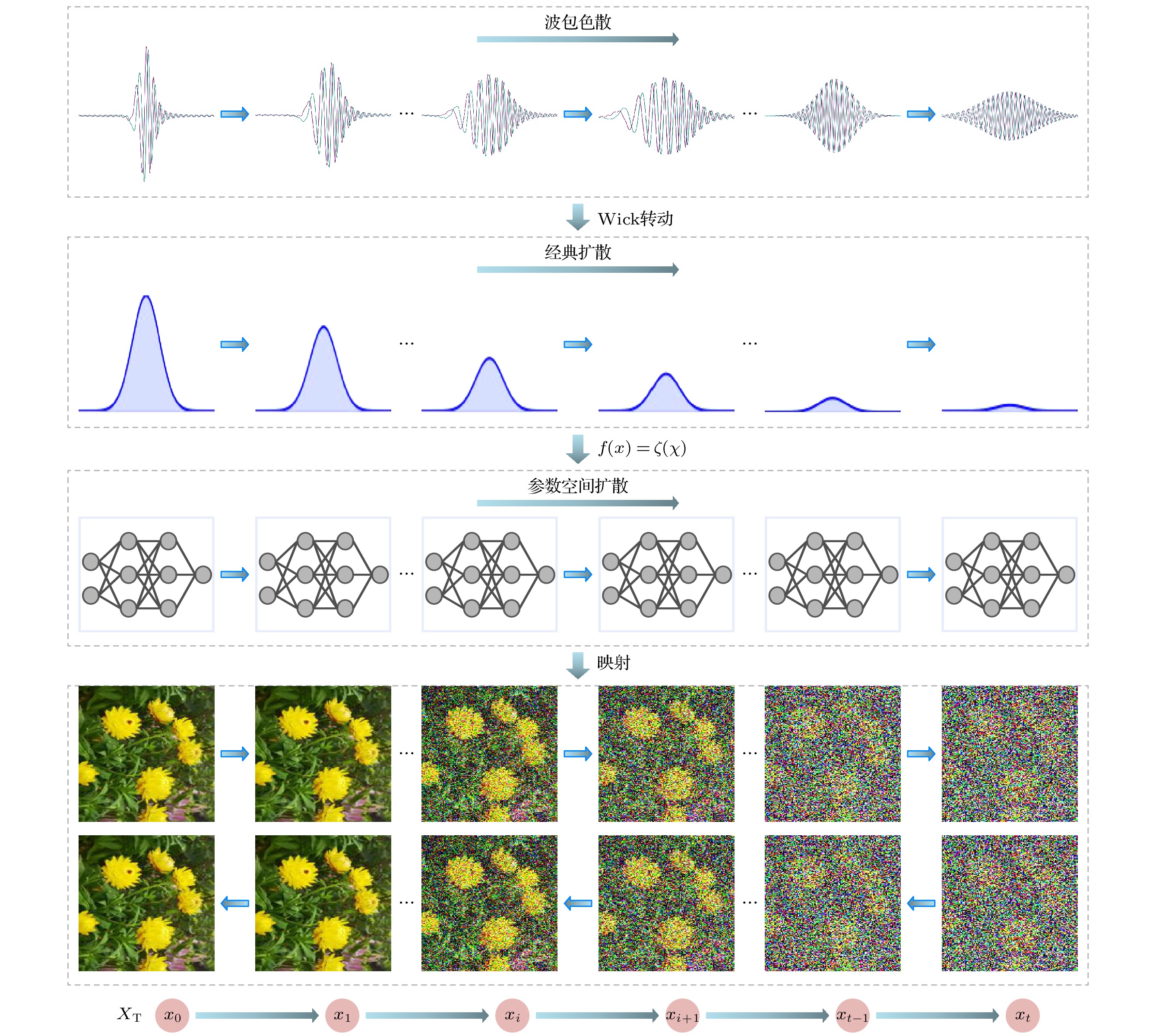
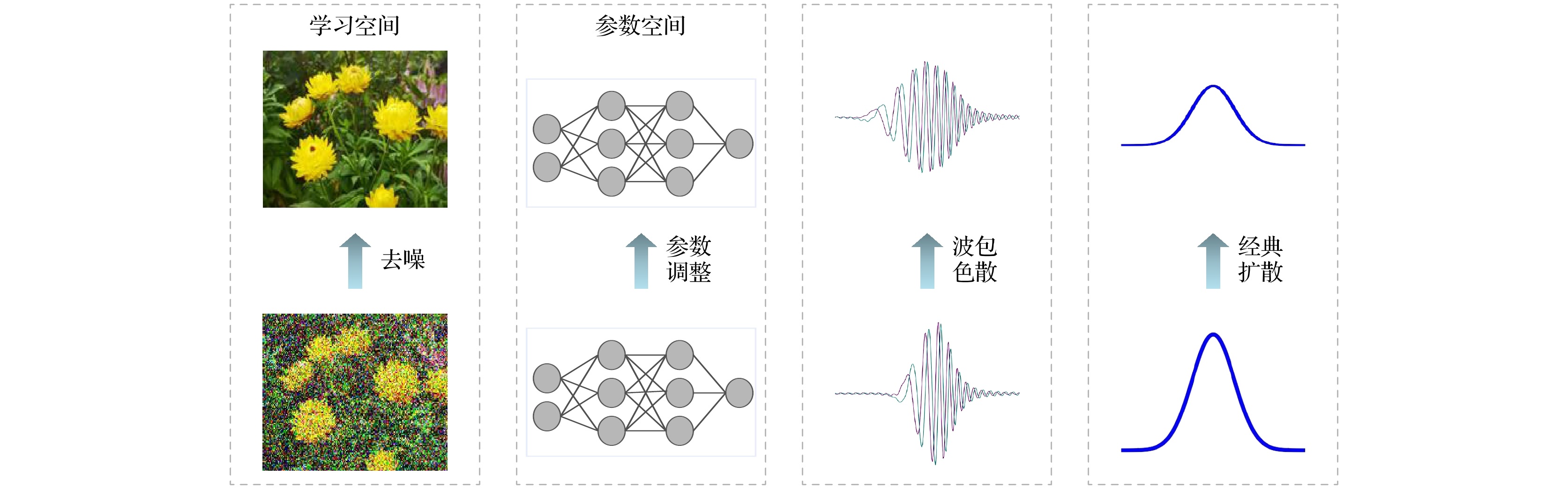
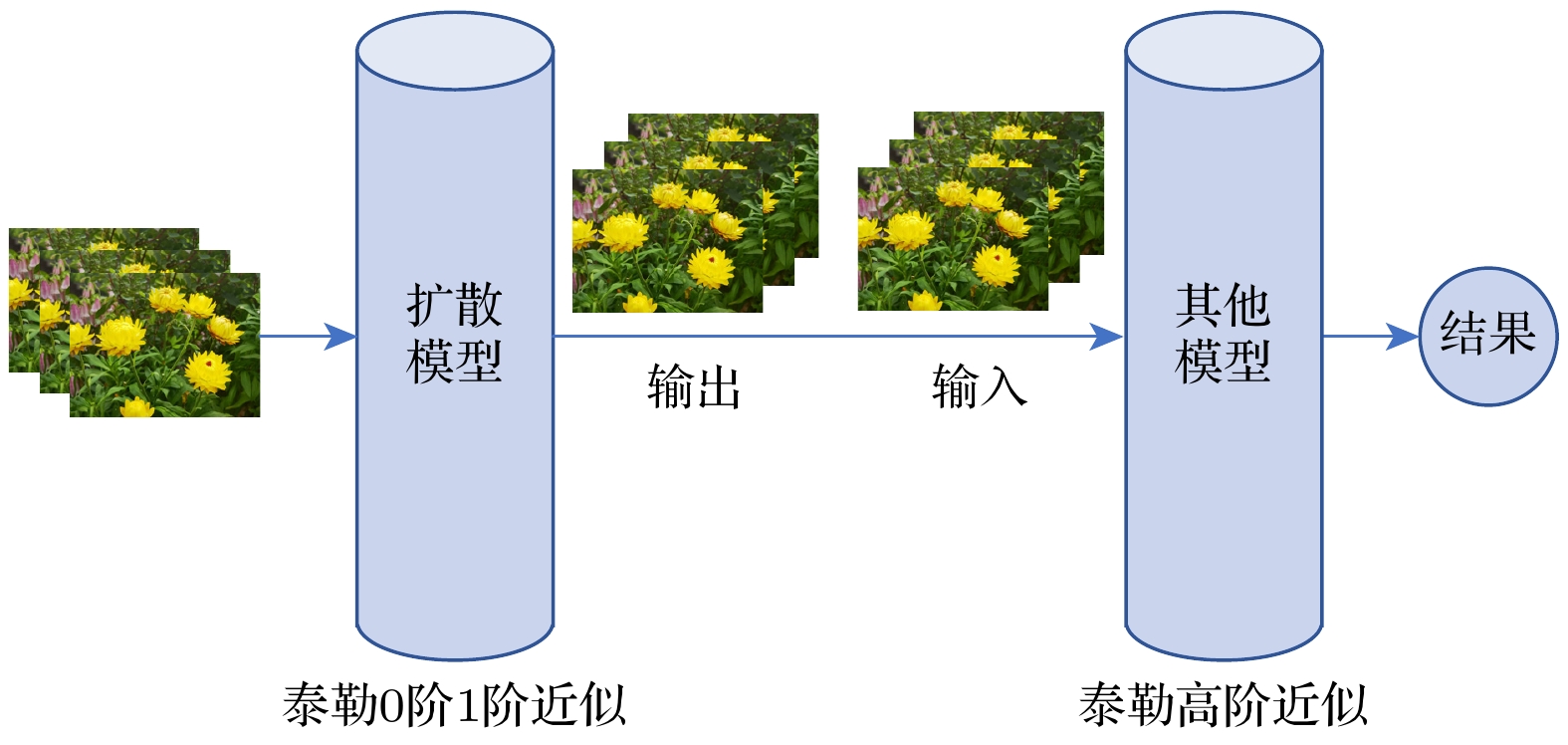
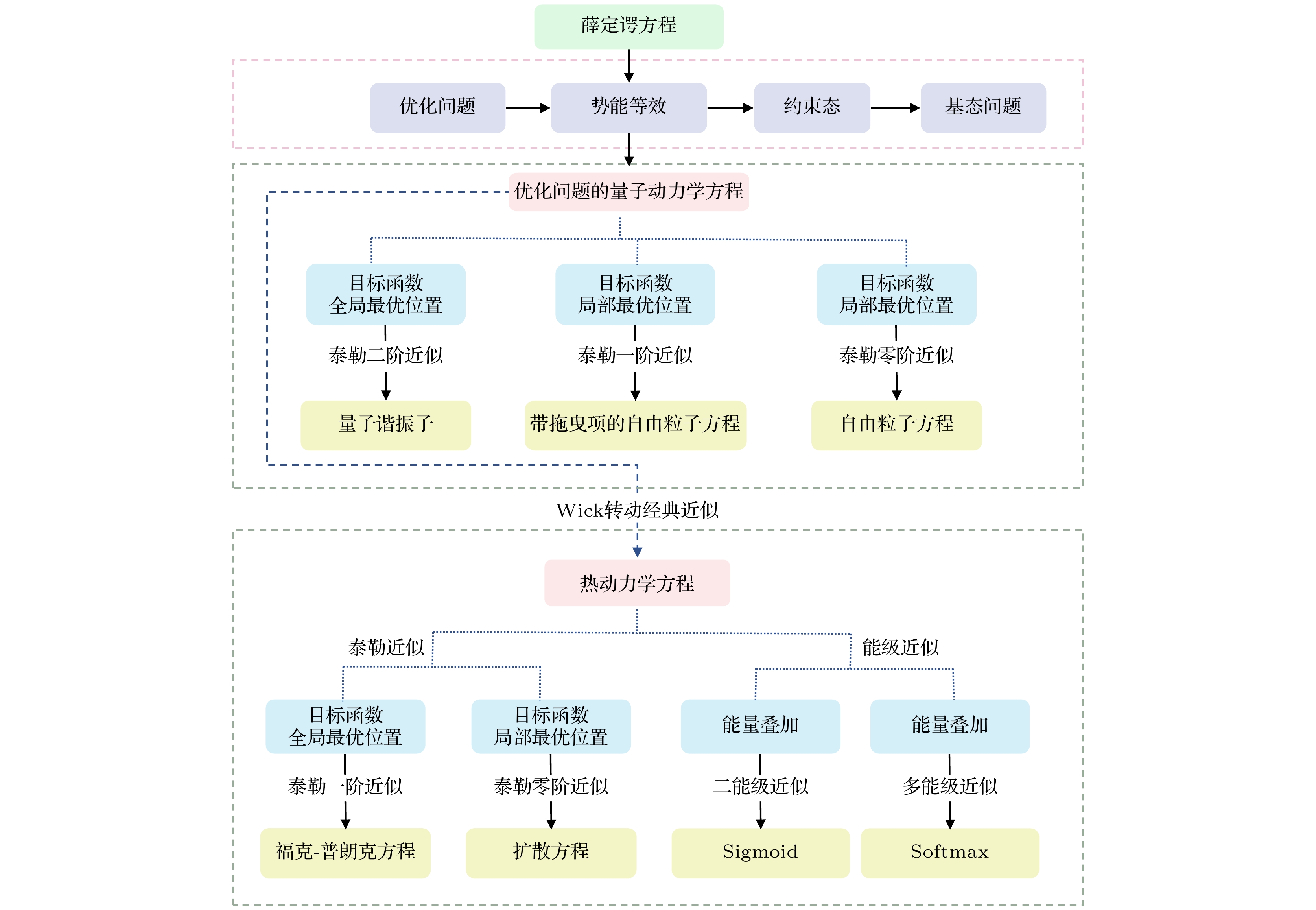
In order to solve the current lack of rigorous theoretical models in the machine learning process, in this paper the iterative motion process of machine learning is modeled by using quantum dynamic method based on the principles of first-principles thinking. This approach treats the iterative evolution of algorithms as a physical motion process, defines a generalized objective function in the parameter space of machine learning algorithms, and regards the iterative process of machine learning as the process of seeking the optimal value of this generalized objective function. In physical terms, this process corresponds to the system reaching its ground energy state. Since the dynamic equation of a quantum system is the Schrödinger equation, we can obtain the quantum dynamic equation that describes the iterative process of machine learning by treating the generalized objective function as the potential energy term in the Schrödinger equation. Therefore, machine learning is the process of seeking the ground energy state of the quantum system constrained by a generalized objective function. The quantum dynamic equation for machine learning transforms the iterative process into a time-dependent partial differential equation for precise mathematical representation, enabling the use of physical and mathematical theories to study the iterative process of machine learning. This provides theoretical support for implementing the iterative process of machine learning by using quantum computers. In order to further explain the iterative process of machine learning on classical computers by using quantum dynamic equation, the Wick rotation is used to transform the quantum dynamic equation into a thermodynamic equation, demonstrating the convergence of the time evolution process in machine learning. The system will be transformed into the ground energy state as time approaches infinity. Taylor expansion is used to approximate the generalized objective function, which has no analytical expression in the parameter space. Under the zero-order Taylor approximation of the generalized objective function, the quantum dynamic equation and thermodynamic equation for machine learning degrade into the free-particle equation and diffusion equation, respectively. This result indicates that the most basic dynamic processes during the iteration of machine learning on quantum computers and classical computers are wave packet dispersion and wave packet diffusion, respectively, thereby explaining, from a dynamic perspective, the basic principles of diffusion models that have been successfully utilized in the generative neural networks in recent years. Diffusion models indirectly realize the thermal diffusion process in the parameter space by adding Gaussian noise to and removing Gaussian noise from the image, thereby optimizing the generalized objective function in the parameter space. The diffusion process is the dynamic process in the zero-order approximation of the generalized objective function. Meanwhile, we also use the thermodynamic equation of machine learning to derive the Softmax function and Sigmoid function, which are commonly used in artificial intelligence. These results show that the quantum dynamic method is an effective theoretical approach to studying the iterative process of machine learning, which provides a rigorous mathematical and physical model for studying the iterative process of machine learning on both quantum computers and classical computers.