-
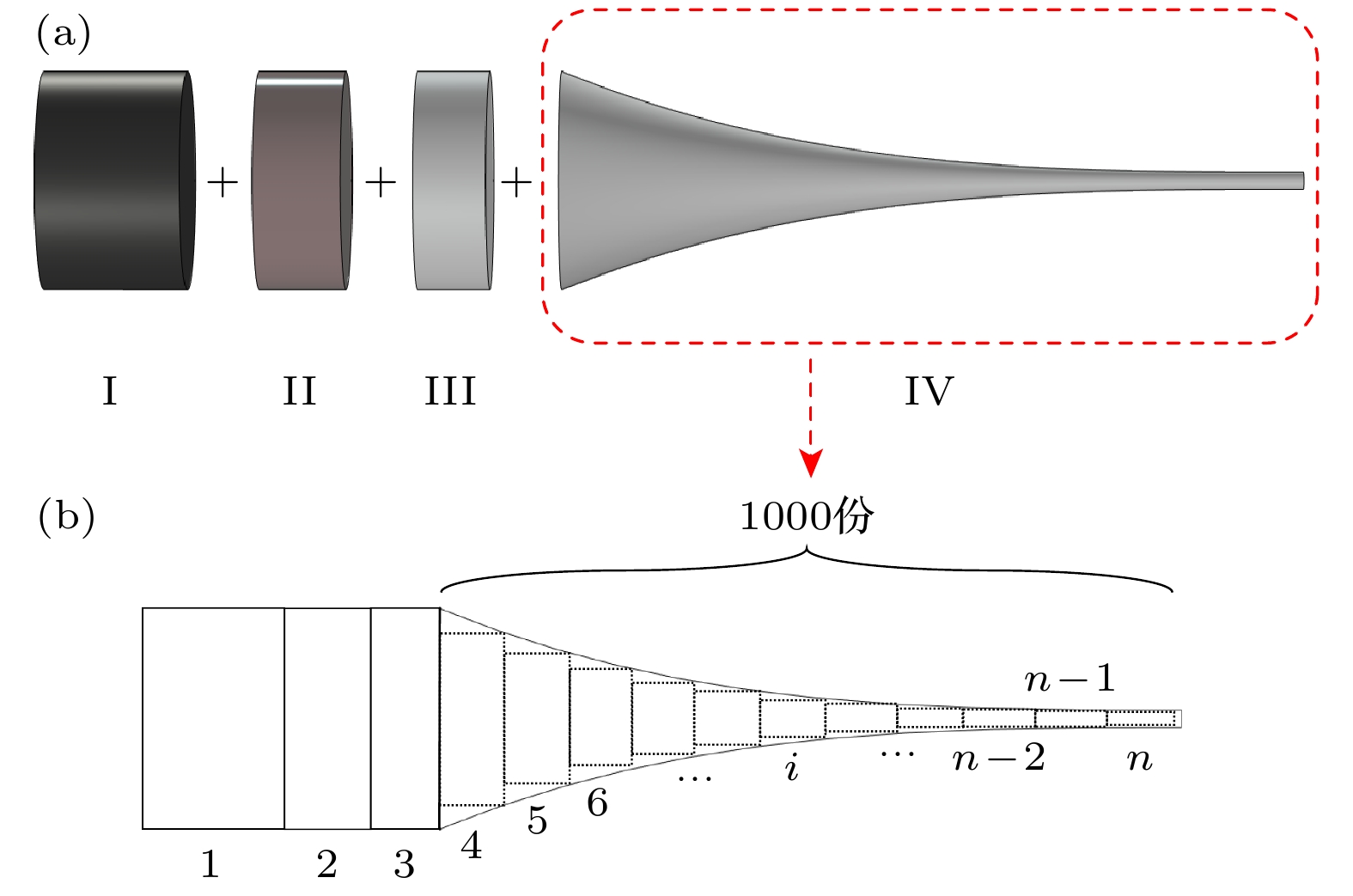
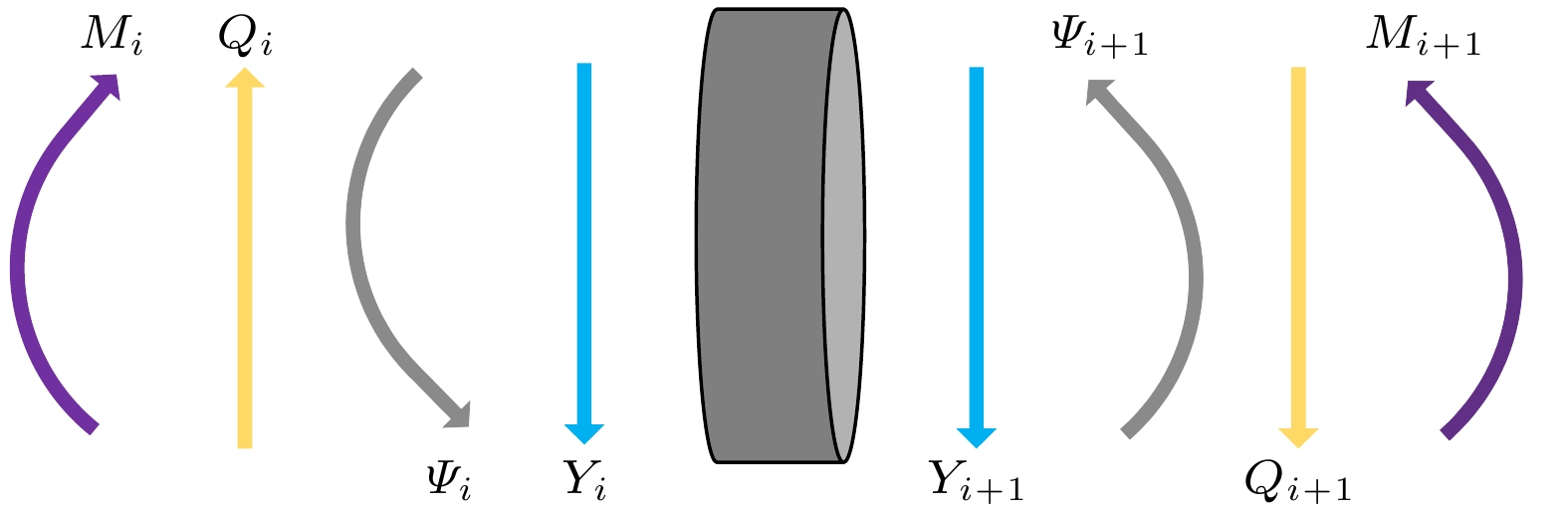
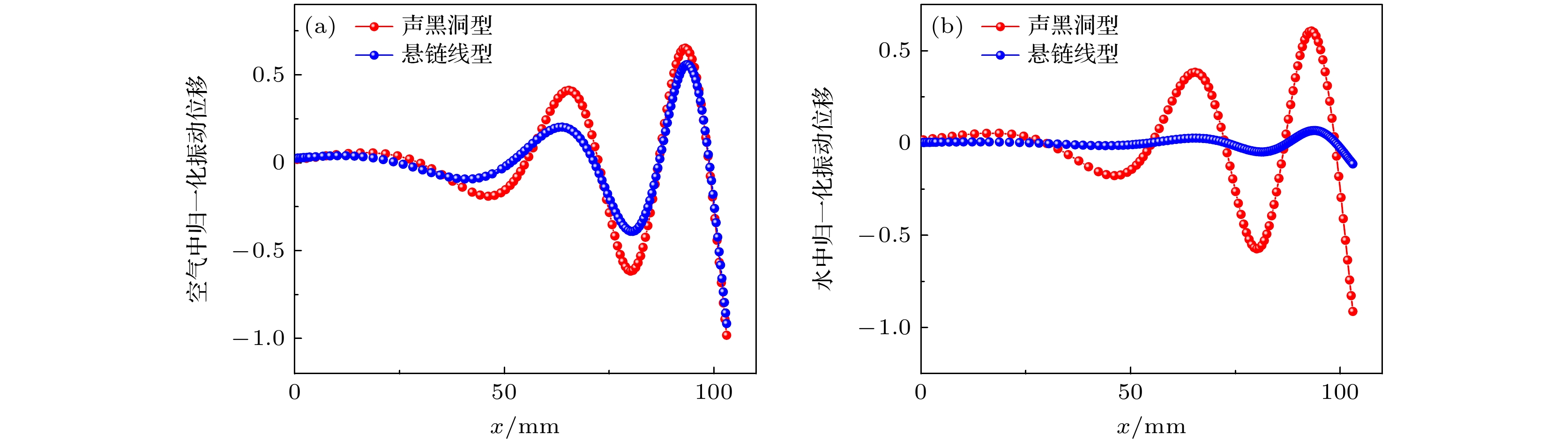
基于声黑洞结构在对弯曲波调控中的能量聚焦与位移放大方面的优势, 提出了一种新型声黑洞夹心式弯曲振动换能器, 该换能器由夹心式弯曲振动换能器与声黑洞探头组成. 基于Timoshenko梁理论, 采用传输矩阵法建立了换能器整体弯曲振动的理论模型, 理论运算得出的解析解与仿真得出的数值解相吻合. 通过有限元方法对该换能器的电阻抗频率响应特性、振动模态、辐射声场和振动位移进行模拟仿真研究, 并与悬链线型换能器进行对比分析. 结果显示, 在相同振动模态下, 声黑洞型换能器的最大声压和振动位移均优于悬链线型换能器, 表明声黑洞结构能够有效提升弯曲振动位移和换能器的侧向辐射性能. 最后加工出了该换能器样机并对其电阻抗特性以及振动模态进行实验测量, 实验结果与仿真结果吻合良好.Based on the advantages of the acoustic black hole (ABH) structure in energy focusing and displacement amplification during the regulation of flexural waves, a new type of ABH sandwich-shaped flexural vibration transducer is proposed in this work. This transducer consists of a sandwich-shaped flexural vibration transducer and an ABH probe. Based on the Timoshenko beam theory, the theoretical model of the overall flexural vibration of the transducer is established by the transfer matrix method, and the calculated results are consistent with the finite element simulation results. The impedance frequency response characteristics, vibration modes, radiation acoustic field and vibration displacement of this transducer are discussed by the finite element method, and a comparative analysis is conducted with the catenary-shaped transducer. The results show that the maximum sound pressure and vibration displacement of the ABH transducer under the same mode are greater than those of the catenary-shaped transducer, indicating that the ABH structure can efficiently enhance the displacement of flexural vibration and the radiation performance of the transducer, and is expected to be utilized as a small-scale acoustic chemical reactor. Finally, a prototype of this transducer is fabricated, then its impedance characteristics and vibration modes are experimentally measured. The experimental results are in agreement with the simulation results.
-
Keywords:
- acoustic black hole structure /
- ultrasonic transducer /
- flexural vibration /
- transfer matrix method
[1] 林书玉 2004 超声换能器的原理及设计 (北京: 科学出版社) 第148页
Lin S Y 2004 The Theory and Design of Ultrasonic Transducers (Beijing: Science Press) p148
[2] Nguyen H T, Nguyen H D, Uan J Y, Wang D A 2014 Ultrasonics 54 2063
 Google Scholar
Google Scholar
[3] 闫久春, 周玉生, 董震, 杨士勤, 周福洪 2001 声学学报 2 104
 Google Scholar
Google Scholar
Yan J C, Zhou Y S, Dong Z, Yang S Q, Zhou F H 2001 Acta Acust. 2 104
 Google Scholar
Google Scholar
[4] Nath C, Rahman M, Neo K S 2009 J. Mater. Process. Tech. 209 4459
 Google Scholar
Google Scholar
[5] Nath C, Rahman M, Neo K S 2009 Int. J. Mach. Tool. Manu. 49 1089
 Google Scholar
Google Scholar
[6] 张德远, 张成茂 2012 中国机械工程 23 39
 Google Scholar
Google Scholar
Zhang D Y, Zhang C M 2012 China Mech. Eng. 23 39
 Google Scholar
Google Scholar
[7] 张园, 康仁科, 刘津廷, 张一鸣, 郑伟帅, 董志刚 2017 机械工程学报 53 33
 Google Scholar
Google Scholar
Zhang Y, Kang R K, Liu J T, Zhang Y M, Zheng W S, Dong Z G 2017 J. Mech. Eng. 53 33
 Google Scholar
Google Scholar
[8] 王剑, 郭吉丰, 鹿存跃, 王文浩, 田创建 2007 声学学报 32 511
 Google Scholar
Google Scholar
Wang J, Guo J F, Lu C Y, Wang W H, Tian C J 2007 Acta Acust. 32 511
 Google Scholar
Google Scholar
[9] Kurosawa M K, Kodaira O, Tsuchitoi Y, Higuchi T 1998 IEEE T. Ultrason. Ferr. 45 1188
 Google Scholar
Google Scholar
[10] Yun C H, Ishii T, Nakamura K, Ueha S, Akashi K 2001 Jpn. J. Appl. Phys. 40 3773
 Google Scholar
Google Scholar
[11] Mironov M A 1988 Sov. Phys. Acoust. 35 176
[12] Mironov M A, Pislyakov V V 2002 Acoust. Phys. 48 347
 Google Scholar
Google Scholar
[13] Hook K, Cheer J, Daley S 2019 J. Acoust. Soc. Am. 145 3488
 Google Scholar
Google Scholar
[14] Ma L, Cheng L 2019 J. Sound Vib. 458 349
 Google Scholar
Google Scholar
[15] Zhao L X, Lai C Q, Yu M 2020 Mech. Syst. Sig. Process. 144 106868
 Google Scholar
Google Scholar
[16] Deng J, Guasch O, Zheng L, Song T T, Cao Y S 2021 J. Sound Vib. 494 115790
 Google Scholar
Google Scholar
[17] 刘洋, 陈诚, 林书玉 2024 物理学报 73 084302
 Google Scholar
Google Scholar
Liu Y, Chen C, Lin S Y 2024 Acta Phys. Sin. 73 084302
 Google Scholar
Google Scholar
[18] 王怡, 陈诚, 林书玉 2025 物理学报 74 044303
 Google Scholar
Google Scholar
Wang Y, Chen C, Lin S Y 2025 Acta Phys. Sin. 74 044303
 Google Scholar
Google Scholar
[19] Remillieux M C, Anderson B E, Le Bas P Y, Ulrich T J 2014 Ultrasonics 54 1409
 Google Scholar
Google Scholar
[20] Chen C, Liu Y, Wang C H, Guo J Z, Lin S Y 2024 Ultrason. Sonochem. 111 107106
 Google Scholar
Google Scholar
[21] Wen S H, Xu L, Gong T, Zhang H D, Liang Z F, Yao L 2025 Appl. Acoust. 239 110826
 Google Scholar
Google Scholar
[22] Zhou G P, Li M X 2000 J. Acoust. Soc. Am. 107 1358
 Google Scholar
Google Scholar
-
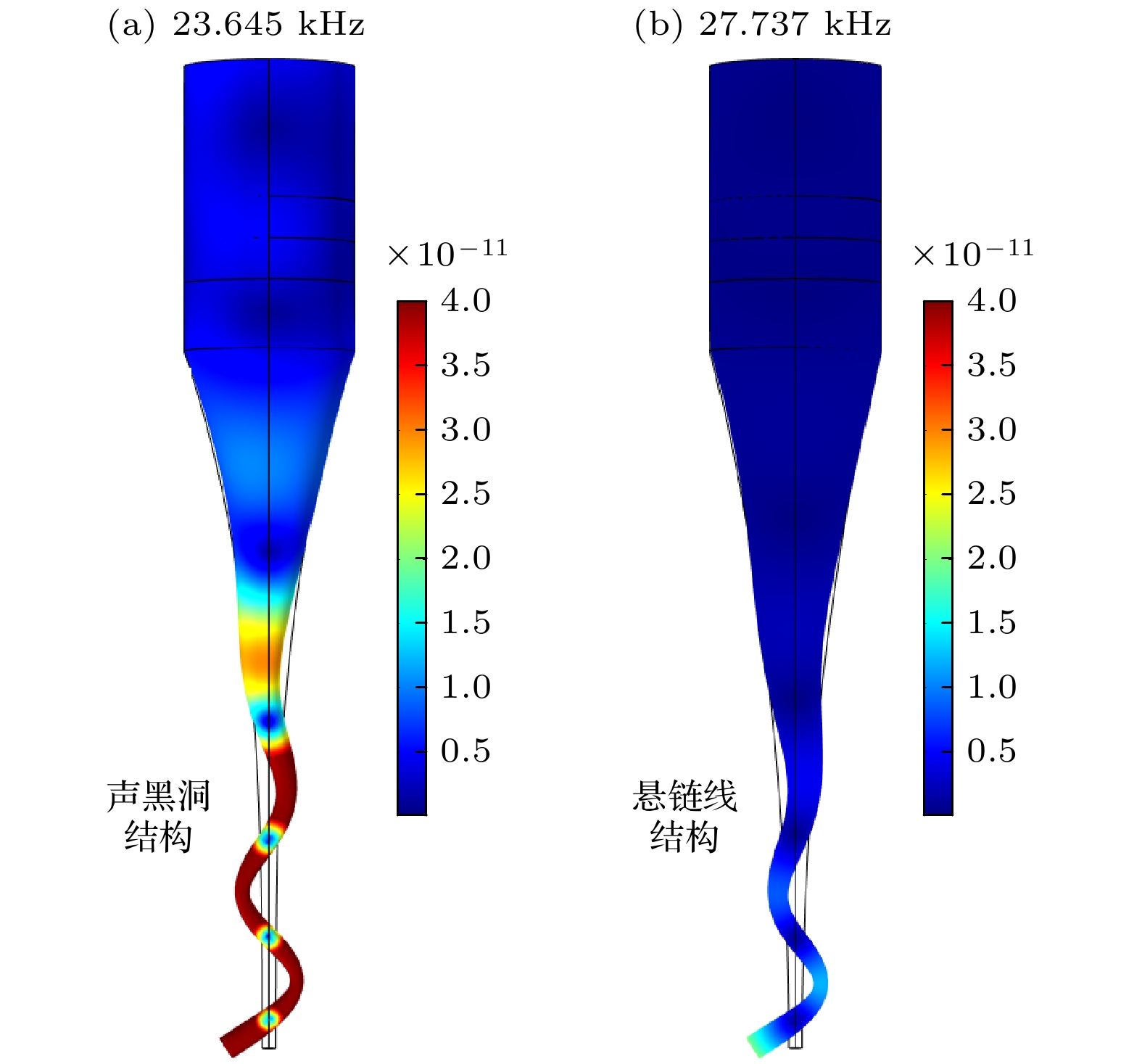
图 5 换能器第六阶弯曲振动模态 (a) 声黑洞型换能器第六阶弯曲振动模态; (b) 悬链线型换能器第六阶弯曲振动模态
Fig. 5. The sixth-order flexural vibration mode of the transducers: (a) The sixth-order flexural vibration mode of the acoustic black hole structure transducer; (b) the sixth-order flexural vibration mode of the catenary-shaped structure transducer.
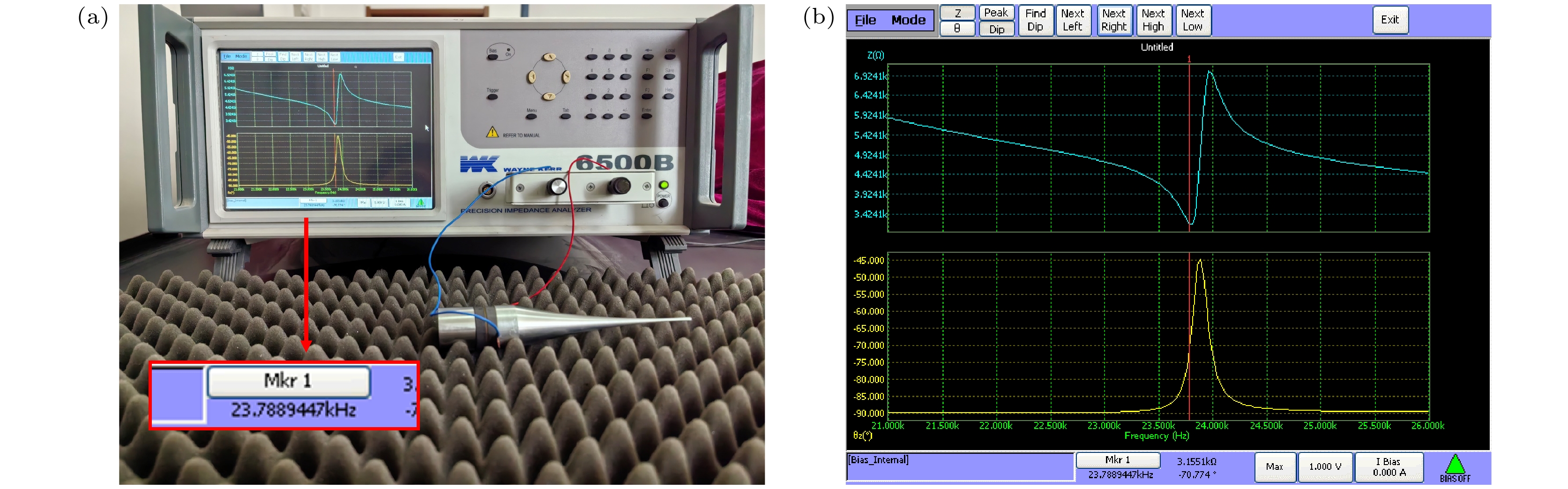
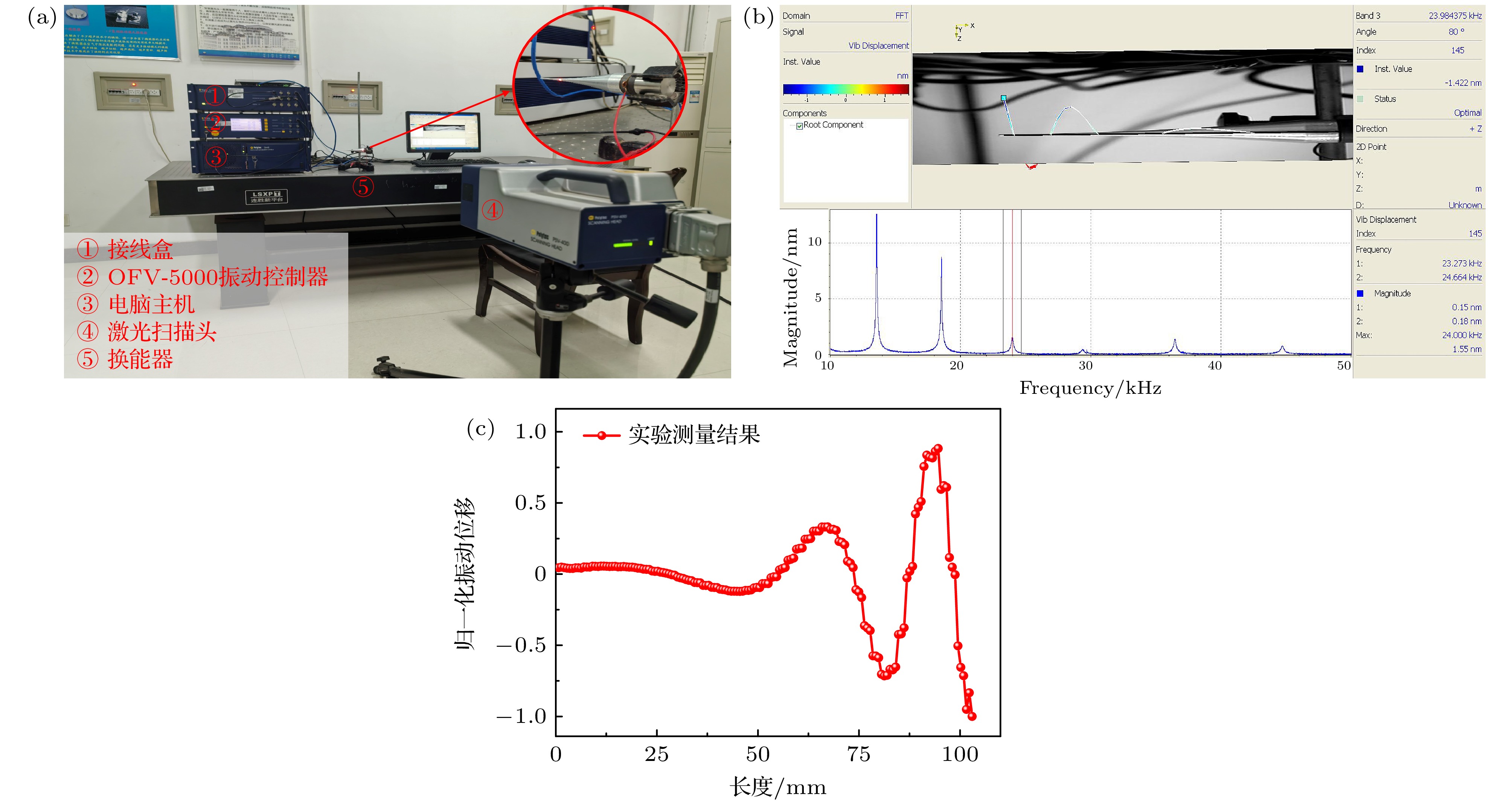
图 11 PSV-400全场扫描式激光振动测量系统及换能器振动模态测量结果 (a) 激光测振实验装置; (b) 换能器弯曲振动模态测量结果; (c) 振动位移分布测量结果
Fig. 11. PSV-400 laser vibrometer measurement system and transducer vibration mode measurement result: (a) Laser vibrometer experimental equipment; (b) measured flexural vibration mode of the transducer; (c) measurement results of vibration displacement distribution.
表 1 m与共振频率的关系
Table 1. Relationship between m and resonant frequency.
悬链线共振
频率/kHz声黑洞共振频率/ kHz m =1.8 m = 2.1 m = 2.4 m = 2.7 m = 3 一阶 2.5 3.1 2.3 1.8 1.5 1.2 二阶 5.9 6.4 5.8 5.3 4.8 4.4 三阶 10.1 10.9 10.0 9.4 8.9 8.4 四阶 15.0 16.1 15.0 14.1 13.5 13.0 五阶 20.8 22.4 20.8 19.6 18.8 17.9 六阶 27.7 29.9 27.7 26.1 24.7 23.7 表 2 换能器材料参数
Table 2. Material parameters of the transducer.
材料 钢 PZT-4 铝 密度/
(kg·m–3)7850 7500 2700 泊松比 0.28 — 0.33 杨氏模量
/GPa或
弹性矩阵
/GPa205 ${\left[ {\begin{array}{*{20}{c}} {139}&{77.8}&{74.3}&0&0&0 \\ {77.8}&{139}&{74.3}&0&0&0 \\ {74.3}&{74.3}&{115}&0&0&0 \\ 0&0&0&{25.6}&0&0 \\ 0&0&0&0&{25.6}&0 \\ 0&0&0&0&0&{30.6} \end{array}} \right]}$ 70 表 3 换能器弯曲振动频率计算结果对比
Table 3. Comparison of calculation results for the flexural vibration frequency of the transducer.
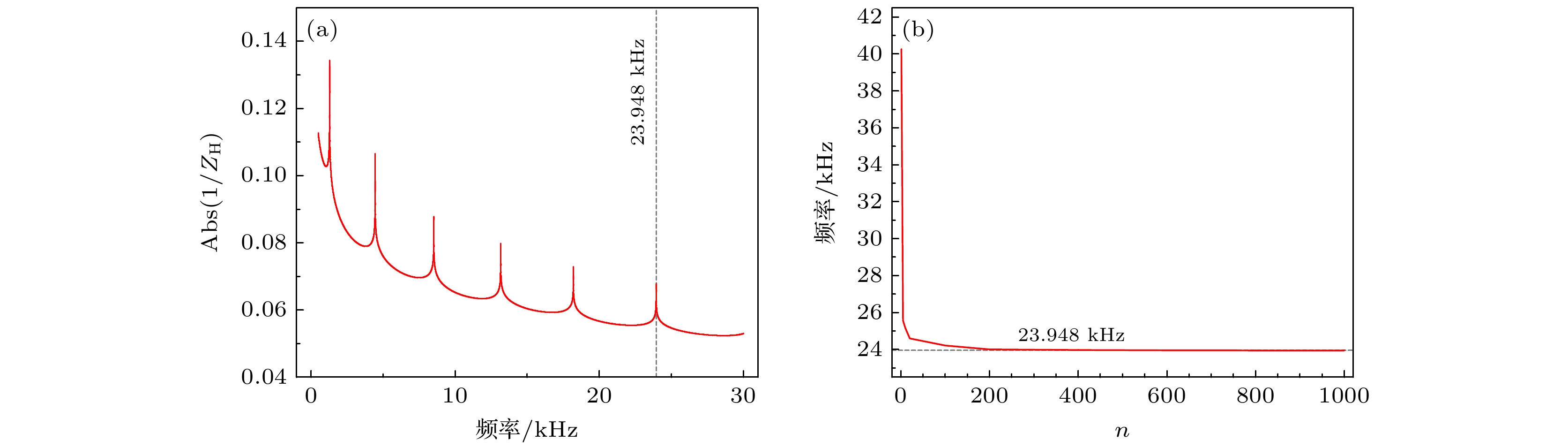
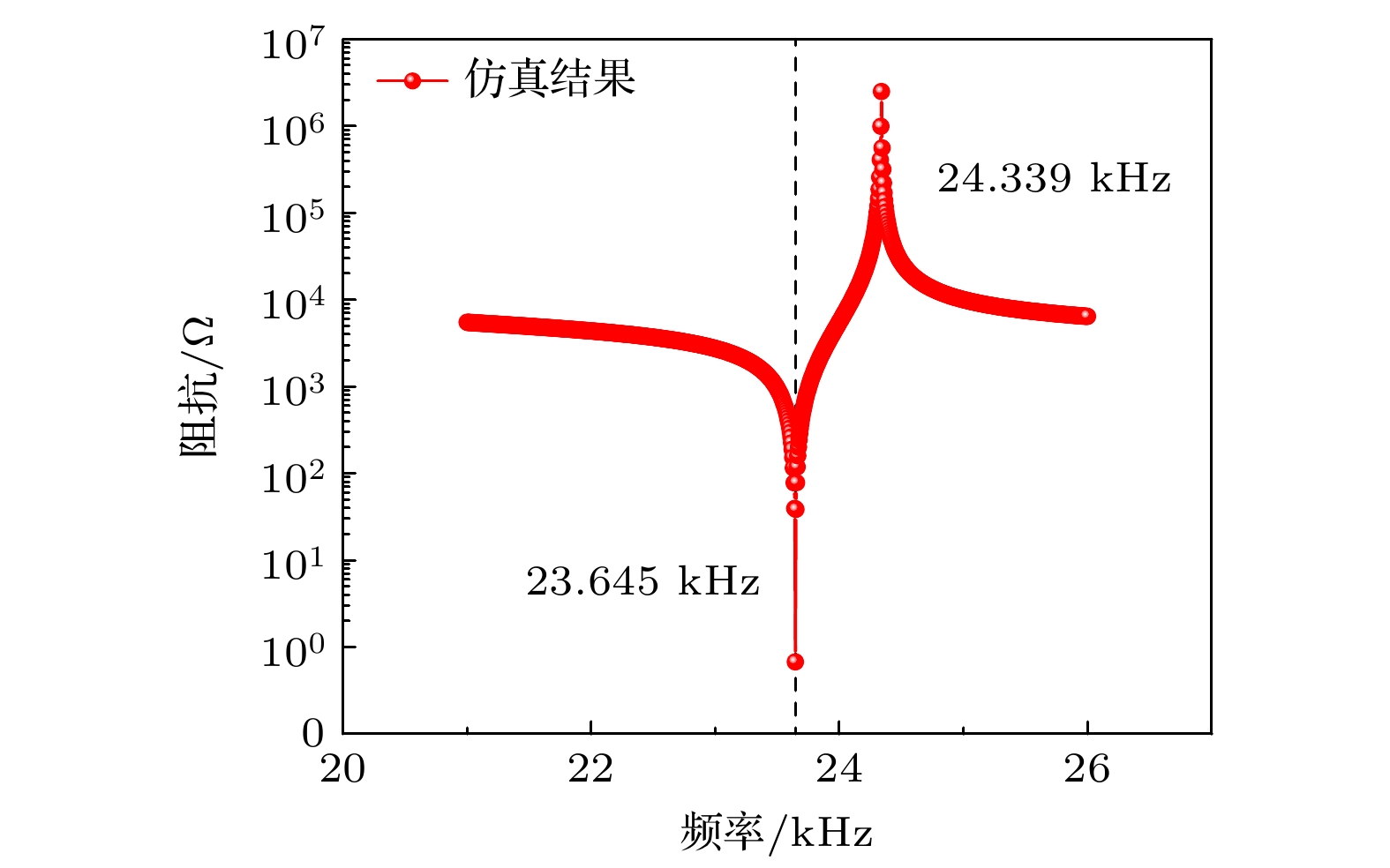
振动频率/kHz 误差/% 理论 仿真 一阶 1.293 1.289 0.31 二阶 4.448 4.432 0.36 三阶 8.518 8.649 1.51 四阶 13.161 13.045 0.88 五阶 18.202 17.979 1.24 六阶 23.948 23.645 1.28 表 4 两种结构的探头不同入水深度对共振频率与最大声压的关系
Table 4. Relationship between the resonant frequency and the maximum sound pressure of two types of probes with different water entry depths.
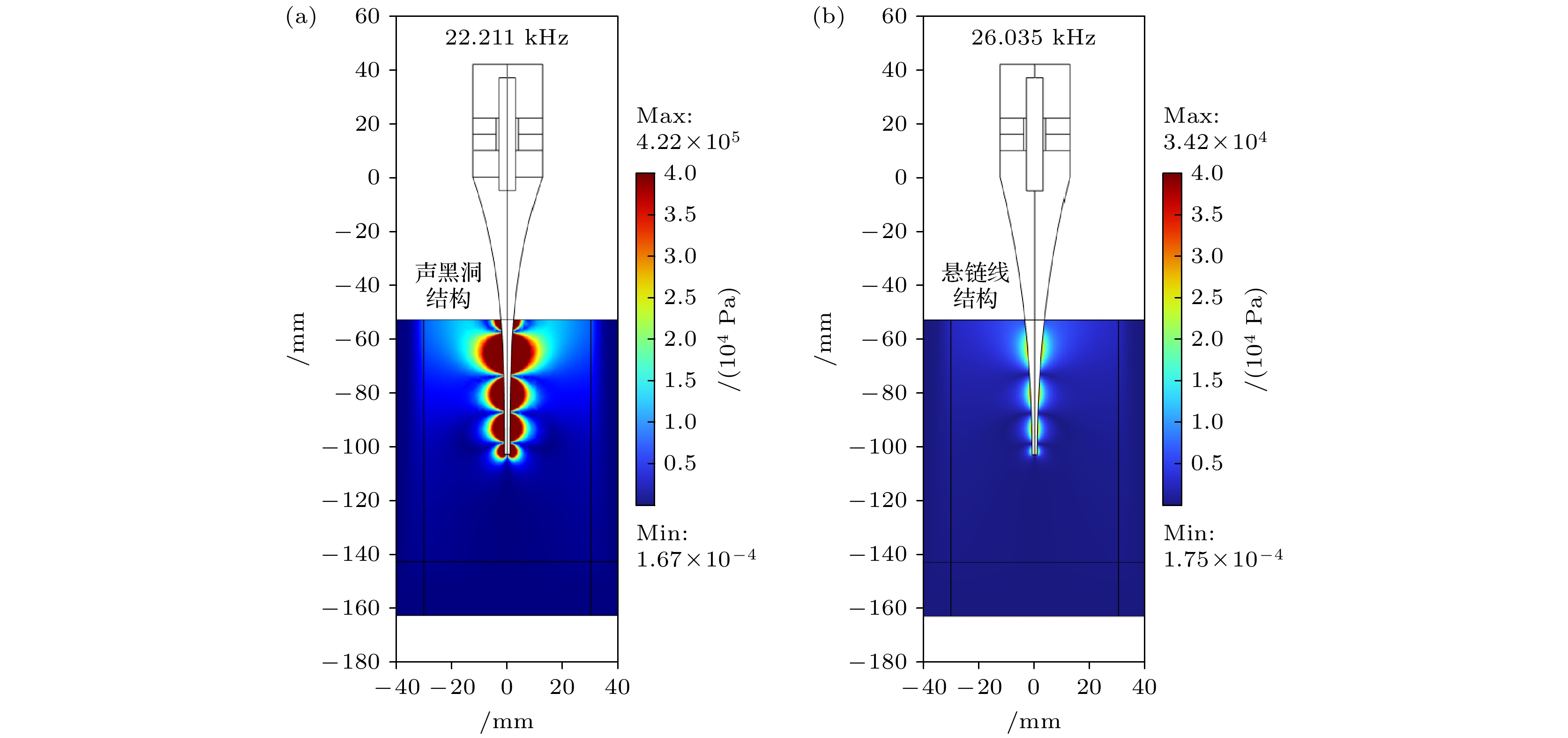
入水深度/mm 声黑洞结构 悬链线结构 共振频率/kHz 最大声压/Pa 共振频率/kHz 最大声压/Pa 25 22.815 9.57×105 26.680 3.01×105 50 22.211 4.22×105 26.035 3.42×104 75 21.719 4.96×104 25.476 6.54×103 -
[1] 林书玉 2004 超声换能器的原理及设计 (北京: 科学出版社) 第148页
Lin S Y 2004 The Theory and Design of Ultrasonic Transducers (Beijing: Science Press) p148
[2] Nguyen H T, Nguyen H D, Uan J Y, Wang D A 2014 Ultrasonics 54 2063
 Google Scholar
Google Scholar
[3] 闫久春, 周玉生, 董震, 杨士勤, 周福洪 2001 声学学报 2 104
 Google Scholar
Google Scholar
Yan J C, Zhou Y S, Dong Z, Yang S Q, Zhou F H 2001 Acta Acust. 2 104
 Google Scholar
Google Scholar
[4] Nath C, Rahman M, Neo K S 2009 J. Mater. Process. Tech. 209 4459
 Google Scholar
Google Scholar
[5] Nath C, Rahman M, Neo K S 2009 Int. J. Mach. Tool. Manu. 49 1089
 Google Scholar
Google Scholar
[6] 张德远, 张成茂 2012 中国机械工程 23 39
 Google Scholar
Google Scholar
Zhang D Y, Zhang C M 2012 China Mech. Eng. 23 39
 Google Scholar
Google Scholar
[7] 张园, 康仁科, 刘津廷, 张一鸣, 郑伟帅, 董志刚 2017 机械工程学报 53 33
 Google Scholar
Google Scholar
Zhang Y, Kang R K, Liu J T, Zhang Y M, Zheng W S, Dong Z G 2017 J. Mech. Eng. 53 33
 Google Scholar
Google Scholar
[8] 王剑, 郭吉丰, 鹿存跃, 王文浩, 田创建 2007 声学学报 32 511
 Google Scholar
Google Scholar
Wang J, Guo J F, Lu C Y, Wang W H, Tian C J 2007 Acta Acust. 32 511
 Google Scholar
Google Scholar
[9] Kurosawa M K, Kodaira O, Tsuchitoi Y, Higuchi T 1998 IEEE T. Ultrason. Ferr. 45 1188
 Google Scholar
Google Scholar
[10] Yun C H, Ishii T, Nakamura K, Ueha S, Akashi K 2001 Jpn. J. Appl. Phys. 40 3773
 Google Scholar
Google Scholar
[11] Mironov M A 1988 Sov. Phys. Acoust. 35 176
[12] Mironov M A, Pislyakov V V 2002 Acoust. Phys. 48 347
 Google Scholar
Google Scholar
[13] Hook K, Cheer J, Daley S 2019 J. Acoust. Soc. Am. 145 3488
 Google Scholar
Google Scholar
[14] Ma L, Cheng L 2019 J. Sound Vib. 458 349
 Google Scholar
Google Scholar
[15] Zhao L X, Lai C Q, Yu M 2020 Mech. Syst. Sig. Process. 144 106868
 Google Scholar
Google Scholar
[16] Deng J, Guasch O, Zheng L, Song T T, Cao Y S 2021 J. Sound Vib. 494 115790
 Google Scholar
Google Scholar
[17] 刘洋, 陈诚, 林书玉 2024 物理学报 73 084302
 Google Scholar
Google Scholar
Liu Y, Chen C, Lin S Y 2024 Acta Phys. Sin. 73 084302
 Google Scholar
Google Scholar
[18] 王怡, 陈诚, 林书玉 2025 物理学报 74 044303
 Google Scholar
Google Scholar
Wang Y, Chen C, Lin S Y 2025 Acta Phys. Sin. 74 044303
 Google Scholar
Google Scholar
[19] Remillieux M C, Anderson B E, Le Bas P Y, Ulrich T J 2014 Ultrasonics 54 1409
 Google Scholar
Google Scholar
[20] Chen C, Liu Y, Wang C H, Guo J Z, Lin S Y 2024 Ultrason. Sonochem. 111 107106
 Google Scholar
Google Scholar
[21] Wen S H, Xu L, Gong T, Zhang H D, Liang Z F, Yao L 2025 Appl. Acoust. 239 110826
 Google Scholar
Google Scholar
[22] Zhou G P, Li M X 2000 J. Acoust. Soc. Am. 107 1358
 Google Scholar
Google Scholar
计量
- 文章访问数: 1815
- PDF下载量: 36
- 被引次数: 0













 下载:
下载: