下载:
-
定向凝固是一种在合金制备的过程中常用的工艺, 其固液界面的传播速度可以受到人为控制. 在定向凝固过程中, 固液界面形态会受到凝固速度的影响. 随着凝固速度的提高, 界面形态将由低速生长的平直界面, 依次演变为小振幅的胞晶界面、大振幅的深胞晶界面、枝晶界面、细胞晶界面, 最后变为高速生长的平直界面. 固液界面形成的典型微结构是枝晶和胞晶, 其生长的稳定性是材料学中重要的研究课题. 合金中胞晶生长的稳定性会影响合金的微结构, 对最终成品合金的性能造成影响. 例如Peng等[1]通过实验发现, 在定向凝固过程中会出现雀斑缺陷, 且凝固过程中的枝晶形貌与Gibbs-Thomson效应密切相关.
许多学者也对晶体生长进行了研究. Mullins和Sekerka[2,3]研究了晶体生长的界面稳定性, 提出了界面稳定性动力理论, 称为M-S理论, 为固液界面形态特征理论奠定了基础. 随后Nash和Glicksman[4]提出最大生长速度理论, 他们在原有的系统上额外加上了两个边界条件并求解了数值解. Kruskal和Segur[5]提出了微观可解性条件(MSC)理论的3个断言, 考虑了各向异性界面能, 在Nash-Glicksman的模型中加入了各向异性参数. Xu等[6,7]提出了界面波(IFW)理论, 该理论对Nash-Glicksman模型进行了重要修正, 使用摄动方法推导出了自由枝晶稳定性生长的理论模型. Pocheau和Georgelin[8]、Ding等[9]通过实验发现了定向凝固中胞晶形态选择具有历史相关性.
另一方面, 界面动力学对于晶体的生长和界面稳定性有着重要影响. Coriell和Sekerka[10]研究发现晶体的界面动力学特性也是影响晶体生长的因素. Trivedi等[11]研究了界面动力学各向异性对定向凝固中胞晶微结构产生的影响, 发现界面动力学各向异性会使得胞晶界面倾斜. 李金富和周尧和[12]通过理论分析, 发现引入动力学项, 扩大了共晶耦合生长的过冷度范围, 降低了共晶生长速度. Tan等[13]研究了Ag-Cu(质量分数为15%)合金的快速定向凝固的枝晶生长模型, 并与实验结果进行对比, 发现引入界面动力学会使得模型与实验结果更接近. 蒋晗等[14]研究了各向异性界面动力学对定向凝固的深胞晶的影响, 发现界面动力学各向异性和表面张力各向异性偏好方向的角度差值不同会影响深胞晶的形态. Chen等[15,16]通过解析方法研究了界面动力学对球晶生长的影响, 发现界面动力学对球晶的生长有较强的稳定作用. 他们发现, 与忽略了界面动力学的情况相比, 界面动力学会使界面过冷度显著减小, 界面更稳定, 这与实验[17,18]的结论一致. 但是, 数值和实验方法并不能解释其内在的机制, 需要使用解析的方法才能解释. 本文将采用多重变量展开法, 对考虑了界面动力学参数的深胞晶界面稳定性进行研究.
-
考虑样本材料细长的二元合金熔体定向凝固过程中的深胞晶生长. 样本位于Hele-shaw生长室, 这是一个细长的生长室, 因此可以看作是二维空间
$ Oxy $ 下的定向凝固过程, 其中原点位于胞晶尖端. 忽略溶质在固相内的扩散, 且除了扩散系数外, 其他热力学性质在固相内相同, 且系统内无对流. 界面提拉速度$ V $ 的方向指向上液相方向. 温度梯度为$ {G}_{T} $ , 浓度为$ C $ , 远场浓度为$ {C}_{\mathrm{\infty }} $ , 胞晶列周期为$ {l}_{\mathrm{w}} $ , 纯熔体温度为$ {T}_{\mathrm{M}0} $ , 溶质扩散率为$ {\kappa }_{\rm D} $ , 溶质扩散长度${l}_{\mathrm{D}}= {{\kappa }_{\mathrm{D}}}/{V}$ , 单位体积内固相产生的潜热为$ {\Delta}H $ , 毛细长度为$ {l}_{\mathrm{c}}=\gamma {c}_{\mathrm{p}}\rho {T}_{\mathrm{M}0} $ , 其中$ \gamma $ 为表面张力,$ \rho $ 为密度,$ {c}_{\mathrm{p}} $ 为比热容. 胞晶生长满足热传导方程、溶质扩散方程和界面方程, 满足热平衡条件、Gibbs-Thomson条件、熵守恒条件、溶质守恒条件和界面分离条件. 然后对系统进行无量纲化, 选取深胞晶尖端半径$ {l}_{\mathrm{t}} $ 为长度尺度,$ V $ 作为速度尺度,${{l}_{\mathrm{t}}}/{V}$ 作为时间尺度. 选取小参数为界面稳定性参数$\varepsilon =\sqrt{\varGamma }=$ $\sqrt{ {{l}_{\mathrm{c}}}/{{l}_{\mathrm{t}}}}$ , Péclet数$Pe = {{l}_{\mathrm{t}}}/{{l}_{\mathrm{D}}}$ , 且有$Pe = \varepsilon \hat{P}e$ , 其中$\widehat{Pe}=$ $O\left(1\right)$ . 无量纲化的温度梯度为$ G=\dfrac{{l}_{\mathrm{D}}}{{\Delta}H/\left({c}_{\mathrm{p}}\rho \right)}{G}_{T} $ , 形态学参数为$ M=-\dfrac{m{C}_{\mathrm{\infty }}}{{\Delta}M/\left({c}_{\mathrm{p}}\rho \right)} $ , 其中$ m < 0 $ 是相图中液相线的斜率. 参数${\lambda }_{\rm G}={{l}_{\rm D}}/{{l}_{\rm G}}$ , 其中${l}_{\rm G}= -m{C}_{\mathrm{\infty }}/$ ${G}_{T}$ . 主间距参数为$W={{l}_{\mathrm{w}}}/{{l}_{\mathrm{t}}}$ , 参数$E= \dfrac{{\Delta}H}{{c}_{\mathrm{p}}\rho {T}_{M}}$ . 于是可以将深胞晶生长满足的热传导方程、溶质扩散方程转化为无量纲的控制方程. 假设深胞晶尖端半径远远小于溶质扩散长度, 即${l}_{\mathrm{t}}\ll {l}_{\rm D}$ . 基于Saffmen-Taylor解构造曲线坐标系[19]$ \left(\xi , \eta \right) $ , 如图1所示. 曲线坐标系与原来的$ \left(x, y\right) $ 平面坐标的关系如下:
图 1 基于Saffmen-Taylor解构造的曲线坐标系
$ \left(\xi , \eta \right) $ [20]Figure 1. Curve coordinate system
$ \left(\xi , \eta \right) $ based on Saffmen-Taylor solution.$ \begin{split}x=\;& WX\left(\xi ,\eta \right) = W\left\{{\lambda }_{0}\xi -\dfrac{2\left(1-{\lambda }_{0}\right)}{\mathrm{\pi }}\right.\\ &\times\left.\mathrm{arctan}\left[\dfrac{\left(1-{\mathrm{e}}^{\mathrm{\pi }\eta }\right)\mathrm{sin}\left(\mathrm{\pi }\mathrm{\xi }\right)}{\left(\mathrm{cos}\left(\mathrm{\pi }\xi \right)+1\right)\left(1+{\mathrm{e}}^{\mathrm{\pi }\eta }\right)}\right]\right\},\end{split} $ $ \begin{split}y=\;& WY\left(\xi ,\eta \right) = W\Bigg[\left(2{\mathrm{\lambda }}_{0}-1\right)\eta \\ & +\dfrac{\left(1-{\lambda }_{0}\right)}{\mathrm{\pi }}\mathrm{ln}\dfrac{{\mathrm{e}}^{2\mathrm{\pi }\eta }+2{\mathrm{e}}^{\mathrm{\pi }\eta }\mathrm{cos}\left(\mathrm{\pi }\xi \right)+1}{4}\Bigg],\end{split} $ 其中
$ {\lambda }_{0} $ 为胞晶的相对宽度, 其与主间距参数W有关. 温度场的线性描述为$T(\xi , \eta , \varepsilon) = \varepsilon \hat{P}[WY(\xi , \eta ) - {y}_{0}]$ .假设胞晶列具有周期性, 每个胞晶宽度都为
$ W $ . 此时只需要考虑单个区间即可. 因此模型等价于在固定侧壁$ x=\pm W $ 的通道中的胞晶生长. 使用曲线坐标系$ \left(\mathrm{\xi }, \mathrm{\eta }\right) $ , 控制方程化为$ \dfrac{{\partial }^{2}C}{\partial {\mathrm{\xi }}^{2}} + \dfrac{{\partial }^{2}C}{\partial {\eta }^{2}} = \varepsilon \widehat{P}e\left({G}^{2}\dfrac{\partial C}{\partial t}-{Y}_{\xi }\dfrac{\partial C}{\partial \xi }-{X}_{\xi }\dfrac{\partial C}{\partial \eta }\right), $ 其中
${M}_{{*}}=\dfrac{V}{\mu {T}_{M}}$ 为界面动力学参数,$ \mu $ 是界面动力学系数. 假设${M}_{{*}}=O({\varepsilon }^{2}) = {\varepsilon }^{2}{m}_{{*}}, {m}_{{*}} = O(1)$ .此外边界条件: 1)远场条件, 当
$ \eta \to \mathrm{\infty } $ 时, 有$ C\to 1 $ ; 2)侧壁区域, 当$ \xi =\pm 1 $ 时有$\dfrac{\partial C}{\partial \mathrm{\xi }}=0$ ; 3)在界面$\eta ={\eta }_{s}\left(\xi , t, \varepsilon\right)$ , 有:$ \begin{split}C=\;&{y}_{\text{*}}-\varepsilon{\mathrm{\lambda }}_{G}W\widehat{P}eY\left(\mathrm{\xi },{\eta }_{s}\right)-\dfrac{{\varepsilon}^{2}}{MW}\big({K}_{0} \\ & +{K}_{1}{\eta }_{s'} +{K}_{2}{{\eta }_{s''}}\big)-\dfrac{{{\varepsilon}}^{2}\widehat{P}e{E}^{-1}{m}_{\text{*}}}{M},\end{split} $ 其中:
$ \begin{split} &{K}_{0}+{K}_{1}{\eta }_{s'}+{K}_{2}{{\eta }_{s''}}= -\dfrac{1}{G\left(\xi ,{\eta }_{s}\right)}\left\{\dfrac{{\eta }_{s''}}{{\left(1+{\eta }_{s'}\right)}^{3/2}}\right. \left.+\;\dfrac{{\Pi }_{0}\left(\xi ,{\eta }_{s}\right)}{{G}^{2}\left(\xi ,{\eta }_{s}\right) {\left(1+{\eta }_{s}^{\text{'2}}\right)}^{1/2}}-\dfrac{{\Pi }_{1}\left(\xi ,{\eta }_{S}\right)}{{G}^{2}\left(\xi ,{\eta }_{s}\right) {\left(1+{\eta }_{s}^{\text{'2}}\right)}^{1/2}}{\eta }_{s'} \right\} \end{split} $ 是两倍平均曲率算子，且有：
$ \begin{split} & {\varPi }_{0} ={Y}_{\xi \xi }{X}_{\xi }-{X}_{\xi \xi }{Y}_{\xi },~~\;{\varPi}_{1}={X}_{\xi \xi }{X}_{\xi }+{Y}_{\xi \xi }{Y}_{\xi },~~ {K}_{0} =-\dfrac{{\varPi }_{0}}{{G}^{3}{\left(1+{\eta }_{s}^{{{\prime}}^{2}}\right)}^{1/2}}, \\ & {K}_{1}=\dfrac{{\varPi }_{1}}{{G}^{3}{\left(1+{\eta }_{s}^{{{\prime}}^{2}}\right)}^{1/2}}, ~~~ {K}_{2} =-\dfrac{1}{{G}^{3}{\left(1+{\eta }_{s}^{{{\prime}}^{2}}\right)}^{3/2}},~~~G=\sqrt{{X}_{\xi }^{2}+{Y}_{\xi }^{2}}. \end{split} $ 质量守恒条件:
$ \begin{split}& \dfrac{\partial C}{\partial \eta }-{\eta }_{s'}\dfrac{\partial C}{\partial \xi } +\varepsilon W\widehat{P}e\left(1-\kappa \right)C \left({G}^{2}\dfrac{\partial {\eta }_{s}}{\partial t}-{Y}_{\xi }{\eta }_{s'}+{Y}_{\eta }\right)=0.\end{split} $ -
将定常胞晶生长的整体基态解作为基态, 则当
$\varepsilon \to 0$ 时, 在界面$\eta = O(1)$ 附近的子区域, 定常解可简化为$ \begin{split}&{C}_{B}\left(\xi ,\eta ,\varepsilon \right)={y}_{\mathrm{*}0}+\varepsilon\widehat{P}e \left\{{y}_{\text{*}1}-W{\lambda }_{G}Y\left(\xi ,\eta \right)+W\eta \left[{\mathrm{\lambda }}_{G}-\left({y}_{\text{*}0}-1\right)\right]\right\}+\cdots ,\end{split} $ 其中:
$ \begin{split} {y}_{\text{*0}}\,&=\dfrac{1+{\lambda }_{G}\left(1-{\lambda }_{0}\right)}{1-{\lambda }_{0}\left(1-\kappa \right)},\;\;{y}_{\text{*1}}=\dfrac{W\left(1-\kappa \right){\lambda }_{0}{\lambda }_{G}{\beta }_{0}}{\left(1-\kappa \right){\lambda }_{0}-1}, ~~ {\beta }_{0} =-\dfrac{2\left(1-{\lambda }_{0}\right)}{\mathrm{\pi }}\mathrm{ln}2,\;\\ {\lambda }_{0}=\;& \dfrac{{y}_{\mathrm{*}0}-1-{\lambda }_{G}}{\left(1-\kappa \right){y}_{\mathrm{*}0}-{\lambda }_{G}}, ~~~ W =\dfrac{\mathrm{\pi }\left(1-{\lambda }_{0}\right)}{2{\lambda }_{0}^{2}}+\cdots ,\;\;\left(\varepsilon \to 0\right) . \end{split}$ 非稳态解可写成两部分:
$ \begin{split}C\left(\xi ,\eta ,t,\varepsilon \right)={C}_{B}\left(\xi ,\eta ,\varepsilon \right)+\widetilde{C}\left(\xi ,\eta ,t,\varepsilon \right),\end{split} $ $ {\eta }_{S}\left(\xi ,t,\varepsilon \right)={\eta }_{B}\left(\xi ,\varepsilon \right)+\widetilde{{\eta }_{s}}\left(\xi ,t,\varepsilon \right). $ 且假设胞晶相对宽度
$ {\mathrm{\lambda }}_{0} $ 是给定的常数, 则主间距$ W $ 和胞晶尖端位置$ {y}_{\text{*}} $ 是无扰动的. 将(7)和(8)式代入系统并进行线性化处理, 得到线性扰动系统. 扰动系统可写为$ \dfrac{{\partial }^{2}\widetilde{C}}{\partial {\mathrm{\xi }}^{2}}+\dfrac{{\partial }^{2}\widetilde{C}}{\partial {\eta }^{2}}=\varepsilon W\widehat{P}e\left( {G}^{2}\dfrac{\partial \widetilde{C}}{\partial t}-{Y}_{\xi }\dfrac{\partial \widetilde{C}}{\partial \xi }-{X}_{\xi }\dfrac{\partial \widetilde{C}}{\partial \eta } \right) . $ 边界条件: 1)远场区域, 当
$ \widetilde{\eta }\to \mathrm{\infty } $ , 有$ \widetilde{C}\to 0 $ ; 2)侧壁区域, 当$ \xi =\pm 1 $ , 有$\dfrac{\partial \widetilde{C}}{\partial \xi }=0$ ; 3)在界面$ \eta ={\eta }_{B} $ 处, 齐次的Gibbs-Thomson条件:$ \dfrac{\partial {C}_{B}}{\partial {\eta }_{B}}\widetilde{{\eta }_{s}} + \widetilde{C} = -\varepsilon {\lambda}_{G}W\widehat{P}e\dfrac{\partial Y\left(\xi ,{\eta }_{B}\right)}{\partial {\eta }_{B}}\widetilde{{\eta }_{s}} -\dfrac{{\mathrm{\varepsilon }}^{2}}{MW} \left\{K\left[{\eta }_{B}\right] + {K}_{1}\widetilde{{\eta }_{s'}}+{K}_{2}\widetilde{\eta }_{s''} + \dfrac{\partial K\left[{\eta }_{B}\right]}{\partial {\eta }_{B}}\widetilde{{\eta }_{s}}\right\} -\dfrac{{\varepsilon }^{2}\widehat{P}{e}^{2}{E}^{-1}{m}_{\text{*}}}{M}. $ 以及齐次的质量守恒条件:
$ \begin{split} &\dfrac{{\partial }^{2}{C}_{B}}{\partial {\eta }_{B}^{2}}\widetilde{{\eta }_{s}}+\dfrac{\partial \widetilde{C}}{\partial {\eta }_{B}}-\dfrac{\partial \widetilde{{\eta }_{s}}}{\partial \xi }\left(\dfrac{\partial {C}_{B}}{\partial \xi }+\dfrac{\partial \widetilde{C}}{\partial \xi }\right)-\dfrac{\partial {\eta }_{B}}{\partial \xi }\dfrac{\partial \widetilde{C}}{\partial \xi } -\dfrac{\partial {\eta }_{B}}{\partial \xi }\widetilde{{\eta }_{s}}\dfrac{{\partial }^{2}{C}_{B}}{\partial \xi \partial \eta } \\ & -\varepsilon W\widehat{P}e\left(1-\mathrm{\kappa }\right)\left(\dfrac{\partial {C}_{B}}{\partial {\eta }_{B}}\widetilde{{\eta }_{s}}+\widetilde{C}\right) \left[{Y}_{\xi }\left(\dfrac{\partial {\eta }_{B}}{\partial \xi }+\dfrac{\partial \widetilde{{\eta }_{S}}}{\partial \xi }\right)-{Y}_{\eta }-{G}^{2}\left(\dfrac{\partial {\eta }_{B}}{\partial t}+\dfrac{\partial \widetilde{{\eta }_{s}}}{\partial t}\right)\right. \left.+\,{Y}_{\xi \eta }\dfrac{\partial {\eta }_{B}}{\partial \xi }\widetilde{{\eta }_{s}}-{Y}_{\eta \eta }\widetilde{{\mathrm{\eta }}_{s}}\right] \\ & -\varepsilon W\widehat{P}e\left(1-\mathrm{\kappa }\right){C}_{B} \left({Y}_{\xi }\dfrac{\partial \widetilde{{\mathrm{\eta }}_{S}}}{\partial \xi }-{G}^{2}\dfrac{\partial \widetilde{{\eta }_{s}}}{\partial t}+{Y}_{\xi \eta }\dfrac{\partial {\eta }_{B}}{\partial \mathrm{\xi }}\widetilde{{\eta }_{s}}-{Y}_{\eta \eta }\widetilde{{\eta }_{s}}\right) +\,\left(h.o.t\right)=0. \end{split} $ -
定义如下的快变量[21]来使用多重变量渐近展开方法:
$ \begin{split} &{t}_+ =\dfrac{\sigma \tau }{\beta \left(\varepsilon \right)}, \\ & {\xi }_+=\dfrac{\varphi \left(\xi ,\eta \right)}{\beta \left(\varepsilon \right)}=\dfrac{1}{\beta \left(\varepsilon \right)}{\int }_{{\xi }_{0}}^{\xi }k\left({\xi }_{1},\eta \right)\text{d}{\xi }_{1}, \\ &{\eta }_+ =\dfrac{\psi \left(\xi ,\eta \right)}{\beta \left(\varepsilon \right)}=\dfrac{1}{\beta \left(\varepsilon \right)}\int_{0}^{ {\eta }}k\left(\xi ,{\eta }_{1}\right)\text{d}{\eta }_{1}, \end{split} $ 其中,
$ \beta \left(\varepsilon \right)=\sqrt{\varepsilon } $ . 同时按照多重变量$ \left(\xi , \eta , {\xi }_{+}, {\eta }_{+}, {t}_{+}\right) $ , 解可写成:$ \begin{split}C\left(\xi ,\eta ,t,\varepsilon \right)&={C}_{B}\left(\xi ,\eta ,\varepsilon \right)+\widetilde{C}\left(\xi ,\eta ,{\xi }_+,{\eta }_+,{t}_+,\varepsilon \right), \\ {\eta }_{s}&={\eta }_{B}\left(\xi ,\varepsilon \right)+\widetilde{{\eta }_{s}}\left(\xi ,{\xi }_+,{t}_+,\varepsilon \right). \\[-10pt]\end{split} $ 利用远场条件、侧壁条件和表面条件, 把系统(9)转变为多变量系统的形式, 且(13)式有如下的渐近展开:
$ \begin{split} &\widetilde{C}\left(\xi ,{\xi }_+,\eta ,{\eta }_+,{t}_+,\varepsilon \right)\sim \\ \;& \varepsilon \big[\widetilde{{\mu }_{0}}\left(\varepsilon \right)\widetilde{{C}_{0}}(\xi ,\eta ,{\xi }_+,{\eta }_+) + \widetilde{{\mu }_{1}}(\varepsilon )\widetilde{{C}_{1}} (\xi ,\eta ,{\xi }_+,{\eta }_+ )\big] {\mathrm{e}}^{{t}_+} \\ & +\cdots , \\ & \widetilde{{\eta }_{s}}\left(\xi ,{\xi }_+,\varepsilon \right) \sim \\ & \left[\widetilde{{b}_{0}}\left(\varepsilon \right)\widetilde{{h}_{0}}\left(\xi ,{\xi }_+\right)+\widetilde{{b}_{1}}\left(\varepsilon \right)\widetilde{{h}_{1}}\left(\xi ,{\xi }_+\right)+\cdots \right]{\text{e}}^{{t}_+}, \\ & k\left(\xi ,\eta ,\varepsilon \right)\sim {k}_{0}\left(\xi ,\eta \right)+\varepsilon {k}_{1}\left(\xi ,\eta \right)+\cdots , \\ & g\left(\xi ,\eta ,\varepsilon \right)\sim {g}_{0}\left(\xi ,\eta \right)+\varepsilon {g}_{1}\left(\xi ,\eta \right)+\cdots , \\ & \; \overline{k}\left(\xi ,\varepsilon \right)\sim \overline{{k}_{0}}\left(\xi \right)+\varepsilon \overline{{k}_{1}}\left(\xi \right)+\cdots , \\ & \sigma \left(\varepsilon \right)\sim {\sigma }_{0}+\varepsilon {\sigma }_{1}+\cdots ,\\[-11pt]\end{split} $ 其中
$\overline{k}=k\left(\xi , 0\right)$ .$ \begin{split}\dfrac{{\partial }^{2}\widetilde{{C}_{0}}}{\partial {\xi }_+^{2}}+\dfrac{{\partial }^{2}\widetilde{{C}_{0}}}{\partial {\eta }_+^{2}}=0.\end{split} $ 边界条件如下: 1)远场区域, 当
$ \eta \to \mathrm{\infty } $ 时, 有$ \widetilde{{C}_{0}} \to 0 $ ; 2)侧壁区域, 当$ \xi =1 $ 时, 有$\dfrac{\partial \widetilde{{C}_{0}}}{\partial {\mathrm{\xi }}_{+}}=0$ ; 3)在界面$ \eta ={\eta }_{+}=0 $ 处, Gibbs-Thomson条件:$ \begin{split}\widetilde{{C}_{0}}=-W\widehat{P}e\left({\lambda }_{G}-{y}_{\text{*0}}+1\right)\widetilde{{h}_{0}}+\dfrac{\overline{{k}_{0}^{2}}}{MW{G}_{0}\left(\xi \right)}\dfrac{{\partial }^{2}\widetilde{{h}_{0}}}{\partial {\xi }_+^{2}},\\\end{split} $ 和质量守恒条件:
$ \begin{split}&\overline{{k}_{0}}\dfrac{\partial \widetilde{{C}_{0}}}{\partial {\eta }_+}+{\mathrm{\sigma }}_{0}W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}\left(\xi \right)\widetilde{{h}_{0}}\\ &+\overline{{k}_{0}}W\widehat{P}e\left[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right]{Y}_{\xi ,0}\left(\xi \right)\dfrac{\partial \widetilde{{h}_{0}}}{\partial {\xi }_+}=0, \end{split}$ 其中
$\overline{{k}_{0}}={k}_{0}\left(\xi , 0\right)$ ;4)尖端条件: 在
$ \xi ={\xi }_{+}=0 $ 处, 有$\widetilde{{h}_{0}}=0, \, \dfrac{\partial \widetilde{{h}_{0}}}{\partial {\xi }_{+}}= 0$ ; 5)根部条件: 当$ {\xi }_{+}\to \mathrm{\infty } $ 时, 有$ \widetilde{{h}_{0}}\to \mathrm{\infty } $ .考虑一般模式的解:
$ \begin{split}\widetilde{{C}_{0}}=\widetilde{{A}_{0}}\mathrm{exp}\left[\text{i}{\xi }_+-{\eta }_+\right],\end{split} $ $ \begin{split}\widetilde{{h}_{0}}=\widehat{{D}_{0}}\mathrm{exp}\left[\text{i}{\xi }_+\right],\end{split} $ 其中系数
$ \widehat{{D}_{0}} $ 是任意常复数.$ \begin{split}{\sigma }_{0}=\dfrac{\overline{{k}_{0}}{\lambda }_{0}}{\overline{{\varLambda }_{0}}{G}_{0}^{2}}-\dfrac{\overline{{k}_{0}^{3}}}{\overline{{\varLambda }_{0}\overline{{\varLambda }_{1}}}{G}_{0}^{3}}+\dfrac{\text{i}\overline{{k}_{0}}{Y}_{\xi ,0}\left(\xi ,0\right)}{\overline{{\varLambda }_{0}}{G}_{0}^{2}},\end{split} $ 其中:
$ \begin{split} \overline{{\varLambda }_{0}}\,&=\dfrac{\left(1-\kappa \right){y}_{\text{*0}}}{\left(1-\kappa \right){y}_{\text{*0}}-{\lambda }_{G}} > 0,\\ \overline{{\Lambda }_{1}} \;&=M{W}^{2}\widehat{P}e\left[\left(1-\kappa \right){y}_{\text{*0}}-{\mathrm{\lambda }}_{G}\right] > 0. \end{split}$ 色散式(20)是
$\overline{{k}_{0}}$ 的三次多项式, 它是Mullins-Sekerka色散公式的归一化. 对于给定的复参数$ {\mathrm{\sigma }}_{0} $ , 可得到3个函数的波函数$\left\{\overline{{k}_{0}^{\left(1\right)}}\left(\xi \right), \overline{{k}_{0}^{\left(2\right)}}\left(\xi \right), \overline{{k}_{0}^{\left(3\right)}}\left(\xi \right)\right\}$ . 色散式(20)展示了胞晶列生长系统内扰动态的界面波特征. -
为了进一步分析色散式(20), 引入新变量
$ \rho $ 来代替$ \xi $ . 令:$ \begin{split}\rho =-\dfrac{{Y}_{\xi ,0}\left(\xi \right)}{{\lambda }_{0}}=\left(\dfrac{1-{\lambda }_{0}}{{\lambda }_{0}}\right)\mathrm{tan}\left(\dfrac{\mathrm{\pi }\xi }{2}\right),\end{split} $ 当
$ \xi \to {1}^{-} $ 时, 有$ \rho \to \mathrm{\infty } $ . 则有$ {G}_{0}\left(\xi \right)={\lambda }_{0}S\left(\rho \right) $ 和$ G\left(\rho \right)=\dfrac{\mathrm{\pi }}{2 a}\left(\rho +\text{i}a\right)\left(\rho -\text{i}a\right) $ , 其中$ a=\dfrac{1-{\mathrm{\lambda }}_{0}}{{\mathrm{\lambda }}_{0}} $ .运用新变量
$ \rho $ , 把色散式(20)转化为$ \begin{split}{\mathrm{\sigma }}_{\mathrm{e}}=\dfrac{{k}_{\mathrm{e}}\left(\rho \right)}{{S}^{2}\left(\rho \right)}\left[\left(1-\text{i}\rho \right)-\dfrac{{k}_{\mathrm{e}}^{2}\left(\rho \right)}{S\left(\rho \right)}\right],\end{split} $ 其中:
$ {k}_{\mathrm{e}}\left(\rho \right)=\dfrac{\widetilde{{k}_{0}}\left(\rho \right)G\left(\rho \right)}{{\mathrm{\lambda }}_{0}\sqrt{\overline{{\varLambda }_{1}}}},{\mathrm{\sigma }}_{\mathrm{e}}=\dfrac{\overline{{\varLambda }_{0}}}{\sqrt{\overline{{\varLambda }_{1}}}}{\mathrm{\sigma }}_{0},S\left(\rho \right)=\sqrt{1+{\rho }^{2}}. $ 给定
$ {\sigma }_{0} $ , 可得以下方程:$ \begin{split}{\mathrm{\sigma }}_{\mathrm{e}}=\dfrac{{k}_{\mathrm{e}}\left(\rho \right)}{{S}^{2}\left(\rho \right)}\left[\left(1-\text{i}\rho \right)-\dfrac{{k}_{\mathrm{e}}^{2}\left(\rho \right)}{S\left(\rho \right)}\right]. \end{split} $ (23)式的3个根为
$\begin{split} {k}_{\mathrm{e}}^{\left(1\right)}\left(\rho \right)&=M\left(\rho \right)\mathrm{cos}\left\{\dfrac{1}{3}\mathrm{arccos}\left[\dfrac{{\mathrm{\sigma }}_{\mathrm{e}}}{N\left(\mathrm{\rho }\right)}\right]\right\}, \\ {k}_{\mathrm{e}}^{\left(2\right)}\left(\rho \right) &=M\left(\rho \right)\mathrm{cos}\left\{\dfrac{1}{3}\mathrm{arccos}\left[\dfrac{{\mathrm{\sigma }}_{\mathrm{e}}}{N\left(\mathrm{\rho }\right)}\right]+\dfrac{2}{3}\mathrm{\pi }\right\}, \\ {k}_{\mathrm{e}}^{\left(3\right)}\left(\rho \right) &=M\left(\rho \right)\mathrm{cos}\left\{\dfrac{1}{3}\mathrm{arccos}\left[\dfrac{{\mathrm{\sigma }}_{\mathrm{e}}}{N\left(\rho \right)}\right]+\dfrac{4}{3}\mathrm{\pi }\right\},\end{split} $ 其中:
$\begin{split} N\left(\rho \right)&=-\dfrac{M\left(\rho \right)\left(1-\text{i}\rho \right)}{3{S}^{2}\left(\rho \right)},\\ M\left(\rho \right)&=\sqrt{\dfrac{4S\left(\rho \right)}{3}}{\left(1-\text{i}\rho \right)}^{1/2}. \end{split} $ 注意到
$ \text{Re}\Big\{\widetilde{{k}_{0}^{(2)}}\Big\} < 0 $ , 因此波函数$ {k}_{\mathrm{e}}^{\left(2\right)}\left(\rho \right) $ 的解$ {H}_{2}\left(\rho \right) $ 给出的扰动态的远场条件不能满足, 需要排除. 因此只有$ {H}_{1}\left(\rho \right)\mathrm{和}{H}_{3}\left(\rho \right) $ 有意义. 从而外部区域的通解可用如下两个界面行波的组合表示:$ \begin{split}\,&\widetilde{{h}_{0}}={D}_{1}\mathrm{exp}\left[\dfrac{\text{i}}{\sqrt{\varepsilon }}{\int }_{{\rho }_{0}}^{\rho }\left(\widetilde{{k}_{0}^{\left(1\right)}}+\varepsilon \widetilde{{k}_{1}^{\left(1\right)}}+\cdots \right)\text{d}{\rho }_{1}\right]\\ &~~+{D}_{3}\mathrm{exp}\left[\dfrac{\text{i}}{\sqrt{\varepsilon }}{\int }_{{\rho }_{0}}^{\rho }\left(\widetilde{{k}_{0}^{\left(3\right)}}+\varepsilon \widetilde{{k}_{1}^{\left(3\right)}}+\cdots \right)\text{d}{\rho }_{3}\right],\end{split} $ 常数
$ \left\{{D}_{1}, {D}_{3}\right\} $ 是在复平面$ \rho $ 上沿着$ \rho $ 的实轴的分片常数. -
一级近似系统的控制方程可写成:
$ \begin{split}\dfrac{{\partial }^{2}\widetilde{{C}_{1}}}{\partial {\xi }_+^{2}}+\dfrac{{\partial }^{2}\widetilde{{C}_{1}}}{\partial {\eta }_+^{2}}=0.\end{split} $ 该系统具有标准模式解:
$ \begin{split} \widetilde{{C}_{1}}=\;&\widetilde{{A}_{1}}\left(\xi ,\eta \right)\mathrm{exp}\left\{\text{i}{\xi }_+-{\eta }_+\right\}, \\ \widetilde{{h}_{1}}=\;&\widetilde{{D}_{1}}\mathrm{exp}\left\{\text{i}{\xi }_+\right\}. \end{split} $ 则由(27)式可得Gibbs-Thomson条件:
$ \begin{split}\widetilde{{A}_{1}}+{J}_{1}\widetilde{{D}_{1}}={I}_{1}\widetilde{{D}_{0}},\end{split} $ 和质量守恒条件:
$ \begin{split}-{k}_{0}\widetilde{{A}_{1}}+{J}_{2}\widetilde{{D}_{1}}={I}_{2}\widetilde{{D}_{0}},\end{split} $ 其中:
$\begin{split} {J}_{1}=\;&\widehat{P}eW\left({\lambda }_{G}-{y}_{\text{*0}}+1\right)+\dfrac{{k}_{0}^{2}}{MW{G}_{0}}, \\ {I}_{1}=\;&-{k}_{0}{h}_{1}\Big[\widehat{P}eW\left({\lambda }_{G}-{y}_{\text{*0}}+1\right) \\ & +\dfrac{{k}_{0}^{2}}{MW{G}_{0}} \left(1-{\alpha }_{4}{B}_{0}\right)\Big] \\ & -\dfrac{2{k}_{0}{k}_{1}}{MW{G}_{0}}-\dfrac{\widehat{P}{e}^{2}{E}^{-1}{m}_{\text{*}}}{M}{k}_{0\text{i}}, \\ {J}_{2}=\;&\widehat{P}eW[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}]{Y}_{\xi }\left(\xi ,0\right){k}_{0\text{i}}\\ &+W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}{\sigma }_{0}, \\ {I}_{2}=\,&-{Q}_{0}+{k}_{0}^{2}{h}_{1} \left[\widehat{P}eW\left({\lambda }_{G}-{y}_{\text{*0}}+1\right)+\dfrac{{k}_{0}^{2}}{MW{G}_{0}}\right] \\ &-{k}_{1}\Big[\widehat{P}eW\left({\lambda }_{G}-{y}_{\text{*0}}+1\right)\\ & +\dfrac{{k}_{0}^{2}}{MW{G}_{0}} +\;\widehat{P}eW{\lambda }_{G}{Y}_{\xi }\left(\xi ,0\right)\text{i}\Big] \\ & +\widehat{P}eW\left[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right] {Y}_{\eta \eta }\left(\xi ,0\right) \\ & -\widehat{P}eW\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}{\sigma }_{1}\\ &+\;W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{Y}_{\xi }\left(\xi ,0\right){k}_{1\text{i}}=0. \end{split} $ 若令(28)和(29)式构成的非齐次线性系统的系数矩阵的行列式为
$ 0 $ , 则$ \left\{\widetilde{{A}_{1}}, \widetilde{{D}_{1}}\right\} $ 有非平凡解的相容性条件为$ \begin{split}{I}_{2}+{k}_{0}{I}_{1}=0.\end{split} $ 将
$ {I}_{1} $ 和$ {I}_{2} $ 代入(30)式, 有:$ \begin{split} \;&{k}_{1}=\dfrac{1}{F\left(\xi \right)}\bigg\{{Q}_{0}-\widehat{P}eW\left[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right]{Y}_{\eta \eta }\left(\xi ,0\right) \\ &~~ +W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}{\sigma }_{1}-{k}_{0\text{i}}^{2}\Big(-\dfrac{\widehat{P}e{E}^{-1}{m}_{\text{*}}}{M} \Big)\bigg\},\\\end{split} $ 其中:
$ \begin{split}F\left(\xi \right)=\;&-\widehat{P}eW\left({\mathrm{\lambda }}_{G}-{y}_{\text{*0}}+1\right)-\dfrac{3{k}_{0}^{2}}{MW{G}_{0}}\\ &+\widehat{P}eW\left[\left(1-\kappa \right){y}_{\text{*0}}-{\mathrm{\lambda }}_{G}\right]{Y}_{\mathrm{\xi }}\left(\mathrm{\xi },0\right)\text{i}. \end{split} $ 这表明解
$ {k}_{1} $ 在函数$ F\left(\xi \right) $ 的解处有奇异性, 它位于$ \xi $ 的扩展复平面$ \zeta =\xi +\text{i}{\xi }_{1} $ 内.将
$ F\left(\xi \right) $ 等函数解析延拓到复平面$ \zeta =\xi +\text{i}{\xi }_{\mathrm{I}} $ 内, 则波函数$\overline{{k}_{0}}\left(\mathrm{\zeta }, 0\right)\equiv \left\{\overline{{k}_{0}^{\left(1\right)}}\left(\xi \right), \overline{{k}_{0}^{\left(2\right)}}\left(\xi \right), \overline{{k}_{0}^{\left(3\right)}}\left(\xi \right)\right\}$ 服从扩展后的色散公式:$ \begin{split} &{\sigma }_{0}= \varSigma \left(\overline{{k}_{0}},\zeta \right)\\=\;&\dfrac{\overline{{k}_{0}}\left(\zeta ,0\right)}{\overline{{\varLambda }_{0}}{G}_{0}^{2}\left(\zeta \right)}\left\{\left[{\lambda }_{0}+\text{i}{Y}_{\xi }\left(\zeta ,0\right)\right]-\dfrac{\overline{{k}_{0}^{2}}\left(\zeta ,0\right)}{\overline{{\varLambda }_{1}}{G}_{0}\left(\zeta \right)}\right\}. \end{split} $ 相应地, 解析函数
$ \widetilde{{k}_{0}}\left(\rho \right)\equiv \left\{\widetilde{{k}_{0}^{\left(1\right)}}\left(\rho \right), \widetilde{{k}_{0}^{\left(2\right)}}\left(\rho \right), \widetilde{{k}_{0}^{\left(3\right)}}\left(\rho \right)\right\} $ 服从色散公式:$ \begin{split}{\mathrm{\sigma }}_{\mathrm{e}}=\dfrac{{k}_{\mathrm{e}}\left(\rho \right)}{{S}^{2}\left(\rho \right)}\left[-\dfrac{{k}_{\mathrm{e}}^{2}\left(\rho \right)}{S\left(\rho \right)}+\left(1-\text{i}\rho \right)\right]. \end{split} $ 用变量
$ \rho $ 表示的奇异点ρc位于复平面$ \rho $ 内, 并且服从方程:$ \begin{split}\left[\widetilde{{k}_{0}^{\left(1\right)}}\left(\rho \right)-\widetilde{{k}_{0}^{\left(3\right)}}\left(\rho \right)\right]=0.\end{split} $ $ \begin{split}{\mathrm{\sigma }}_{\mathrm{e}}=\dfrac{2}{\sqrt{27}}{\left(\dfrac{1-\text{i}\text{ρ}\text{c}}{1+\text{i}\text{ρ}\text{c}}\right)}^{3/4}=\dfrac{\overline{{\varLambda }_{0}}}{\sqrt{\overline{{\varLambda }_{1}}}}{\mathrm{\sigma }}_{0}. \end{split} $ 由(36)式可得到3个复奇异点, 它们的位置与
$ {\mathrm{\sigma }}_{0} $ ,$ \overline{{\varLambda }_{0}} $ 和$ \overline{{\varLambda }_{1}} $ 有关. -
对固定的
$ {\sigma }_{0} $ , 通过对色散式(33)求关于$ \zeta $ 的全导数和偏导数, 对(32)式求导, 可得:$ \begin{split} {F}' (\zeta)={F}_{0'}(\zeta ) -\dfrac{3{k}_{0}}{MW{G}_{0}}\left(2\dfrac{{R}_{0} (\zeta )}{F(\zeta )}-\dfrac{{G}_{0'}}{{G}_{0}}\right). \end{split} $ 因此, 当
$ \zeta ={\zeta }_{\mathrm{c}} $ 时, (31)式化解为$ \begin{split}{k}_{1}\left(\xi \right)=\dfrac{{R}_{1}\left(\xi \right)}{F\left(\xi \right)}-\text{i}\dfrac{{R}_{2}\left(\xi \right)}{F\left(\xi \right)}\dfrac{{k}_{0'}\left(\xi \right)}{{k}_{0}\left(\xi \right)},\end{split} $ 其中:
$ \begin{split} &{R}_{1}\left(\xi \right)=-\dfrac{\text{i}{k}_{0}^{2}}{MW}\dfrac{\partial }{\partial \xi }\left[\dfrac{1}{{G}_{0}\left(\xi \right)}\right]\\ &~~-\widehat{P}eW\left[{\mathrm{\lambda }}_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right] {Y}_{\eta \eta }\left(\xi ,0\right) \\ &~~+W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}{\mathrm{\sigma }}_{1}-{k}_{0\text{i}}^{2}\left[-\dfrac{\widehat{P}e{E}^{-1}{m}_{\text{*}}}{M}\right], \\ & \ \ \ \ \ {R}_{2}\left(\xi \right)=\dfrac{2{k}_{0}^{2}}{MW{G}_{0}\left(\xi \right)}. \end{split} $ 从(38)式可知, 当
$ \zeta $ 趋于孤立奇点$ {\zeta }_{\mathrm{c}} $ 时, 有:$ \begin{split}{k}_{1}\left(\zeta \right)=\dfrac{{m}_{1}{R}_{1}\left({\zeta }_{\mathrm{c}}\right)}{{\left(\zeta -{\zeta }_{\mathrm{c}}\right)}^{1/2}}+\dfrac{{m}_{2}}{\zeta -{\zeta }_{\mathrm{c}}},\end{split} $ 其中
$ {m}_{1}={m}_{2}=O\left(1\right) $ .函数
$ {k}_{1}\left(\zeta \right) $ 在奇点附近可展开为Laurent级数. 由(39) 式,$ {R}_{1}\left({\zeta }_{\mathrm{c}}\right)=0 $ , 且$ {\zeta }_{\mathrm{c}} $ 是函数$ {k}_{1}\left(\zeta \right) $ 的单极点, 由此得$ {\mathrm{\sigma }}_{1} $ 为$ \begin{split}{\mathrm{\sigma }}_{1}=\;&\dfrac{1}{W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{G}_{0}^{2}\left({\zeta }_{\mathrm{c}}\right)}\left\{-\text{i}\dfrac{{F}_{0}\left({\zeta }_{\mathrm{c}}\right)}{3}\dfrac{{G}_{0'}\left({\zeta }_{\mathrm{c}}\right)}{{G}_{0}\left({\zeta }_{\mathrm{c}}\right)}\right.\\ &+\widehat{P}eW\left[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right]{Y}_{\eta \eta }\left({\zeta }_{\mathrm{c}},0\right) \\ &\left.-\;\text{i}\dfrac{{F}_{0}\left({\zeta }_{\mathrm{c}}\right)\widehat{P}e{E}^{-1}{m}_{\text{*}}W{G}_{0}\left({\zeta }_{\mathrm{c}}\right)}{3}\right\}.\\[-20pt] \end{split} $ 由(40)式
$ {\sigma }_{1} $ 由自由参数$ {\sigma }_{0} $ 确定. 接下来将研究奇异点$ {\zeta }_{\mathrm{c}} $ 附近的行为, 导出$ {\sigma }_{0} $ 的表达式, 扩展$ \left(\xi , \eta \right) $ 平面内的全局波模式解. -
为求解
$ \left({\zeta }_{\mathrm{c}}, 0\right) $ 附近的内解, 在齐次系统内引进内变量:$ \begin{split}{\zeta }_{\text{*}}=\dfrac{\zeta -{\zeta }_{\mathrm{c}}}{{\varepsilon }^{\alpha }},\end{split} $ $ \begin{split}{\eta }_{\text{*}}=\dfrac{\eta }{{\varepsilon }^{\alpha }},\end{split} $ 其中
$ \alpha $ 待定. 使用上述内变量后, 内解的控制方程变为$ \begin{split}&\dfrac{{\partial }^{2}\widetilde{{C}_{\text{*}}}}{\partial {\mathrm{\zeta }}_{\text{*}}^{2}} +\dfrac{{\partial }^{2}\widetilde{{C}_{\text{*}}}}{\partial {\eta }_{\text{*}}^{2}} +{\varepsilon }^{\alpha +1}W\widehat{P}e \bigg[ {Y}_{\xi }\dfrac{\partial \widetilde{{C}_{\text{*}}}}{\partial {\zeta }_{*}} \\ & +{X}_{\xi }\dfrac{\partial \widetilde{{C}_{\text{*}}}}{\partial {\eta }_{*}}-{G}^{2}\dfrac{\sigma }{\beta \left(\varepsilon \right)}\dfrac{\partial \widetilde{{C}_{*}}}{\partial {t}_+} \bigg]=0.\end{split} $ 界面条件为当
$ {\eta }_{\text{*}}=0 $ 时, 有Gibbs-Thomson条件:$ \begin{split} \;& \widetilde{{C}_{*}}{\varepsilon }^{\alpha }=-\varepsilon \widehat{P}eW\left[{\lambda }_{G}-\left({y}_{\text{*0}}-1\right)\right]\widetilde{{\eta }_{\text{*}s}}{\varepsilon }^{\alpha } \\ &~~ -\;\dfrac{{\varepsilon }^{2}}{MW}\left\{-\dfrac{1}{{\varepsilon }^{\alpha }{G}_{0}}\widetilde{{\eta }_{\text{*}s}^{''}}+\dfrac{\partial K\left[0\right]}{\partial {\eta }_{B}}{\varepsilon }^{\alpha }\widetilde{{\eta }_{*s}}\right\},\end{split} $ 和质量守恒条件:
$ \begin{split}&-\varepsilon \widehat{P}eW{\lambda }_{G}{Y}_{\eta \eta }\left(\xi ,0\right){\varepsilon }^{\alpha }\widetilde{{\eta }_{*s}}+\dfrac{\partial \widetilde{{C}_{\text{*}}}}{\partial {\eta }_{\text{*}}}+\varepsilon \widehat{P}eW{\lambda }_{G}\\ &\times{Y}_{\xi}\left(\xi ,0\right)\dfrac{\partial \widetilde{{\eta }_{*s}}}{\partial {\zeta }_{*}} +{\varepsilon }^{\alpha +1}{Y}_{\eta }W\widehat{P}e\left(1-\kappa \right)\left\{\varepsilon \widehat{P}eW\right.\\ &\left.\times\left[-{\lambda }_{G}{Y}_{\eta }\left(\xi ,0\right)+{\lambda }_{G}-\left({y}_{\text{*0}}-1\right)\right]\widetilde{{\eta }_{*s}}+\widetilde{{C}_{*}}\right\} \\ &-\varepsilon W\widehat{P}e\left(1-\kappa \right){C}_{B}{Y}_{\xi }\left(\xi ,0\right)\dfrac{\partial \widetilde{{\eta }_{*s}}}{\partial {\zeta }_{*}}+{\varepsilon }^{\alpha +1}W\widehat{P}e\\ &\times\left(1-\kappa \right){C}_{B}{G}^{2}\dfrac{\sigma }{\beta \left(\varepsilon \right)}\dfrac{\partial \widetilde{{\eta }_{*s}}}{\partial {t}_+} +{\varepsilon }^{\alpha +1}W\widehat{P}e\left(1-\kappa \right)\\ &\times{C}_{B}{Y}_{\eta \eta }\widetilde{{\eta }_{\mathrm{*}s}} +\left(h.o.t\right)=0.\\[-13pt]\end{split} $ 然后把内解进行渐近展开:
$ \begin{split}&\widetilde{{C}_{*}}\left({\zeta }_{*},{\eta }_{*},{t}_+,\varepsilon \right)=\\ &\varepsilon \left[\widetilde{{v}_{0}}\left(\varepsilon \right)\widetilde{{C}_{*0}}\left({\zeta }_{*},{\eta }_{*}\right)+\widetilde{{v}_{1}}\left(\varepsilon \right)\widetilde{{C}_{*1}}\left({\zeta }_{*},{\eta }_{*}\right)+\cdots \right]{\mathrm{e}}^{{t}_+},\end{split} $ $ \begin{split}&\widetilde{{\eta }_{*s}}\left({\zeta }_{*},{t}_+,\varepsilon \right)=\\ &\left[\widetilde{{v}_{0}}\left(\varepsilon \right)\widetilde{{h}_{*0}}\left({\zeta }_{*}\right)+\widetilde{{v}_{1}}\left(\varepsilon \right)\widetilde{{h}_{*1}}\left({\zeta }_{*}\right)+\cdots \right]{\mathrm{e}}^{{t}_+}. \end{split} $ 去掉内解系统里的高阶无穷小, 可得内解首级近似下的控制方程:
$ \begin{split}\dfrac{{\partial }^{2}\widetilde{{C}_{*0}}}{\partial {\zeta }_{*}^{2}}+\dfrac{{\partial }^{2}\widetilde{{C}_{*0}}}{\partial {\eta }_{*}^{2}}=0.\end{split} $ 界面条件为当
$ {\eta }_{*}=0 $ 时, 有Gibbs-Thomson条件:$ \begin{split}\widetilde{{C}_{*0}}=-\widehat{P}eW\left[{\lambda }_{G}-\left({y}_{\text{*0}}-1\right)\right]\widetilde{{h}_{*0}}+\dfrac{{\varepsilon }^{1-2\mathrm{\alpha }}}{MW{G}_{0}}\dfrac{{\partial }^{2}\widetilde{{h}_{*0}}}{\partial {\zeta }_{*}^{2}},\\\end{split} $ 和质量守恒条件:
$ \begin{split}&\dfrac{\partial \widetilde{{C}_{*0}}}{\partial {\eta }_{*}}+\widehat{P}eW\left[{\lambda }_{G}-\left(1-\kappa \right){y}_{\text{*0}}\right]{Y}_{\xi }\left(\xi ,0\right)\dfrac{\partial \widetilde{{h}_{*0}}}{\partial {\zeta }_{*}}\\ &+\;{\varepsilon }^{\alpha -\tfrac{1}{2}}W\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{\sigma }_{0}{G}_{0}^{2}\widetilde{{h}_{*0}}=0.\end{split} $ 由解的解析性, 可得
$\dfrac{\partial \widetilde{{C}_{*0}}}{\partial {\eta }_{*}}=\text{i}\dfrac{\partial \widetilde{{C}_{*0}}}{\partial {\zeta }_{*}}$ . 再运用变量$ \rho = -\dfrac{{Y}_{\xi }\left(\xi , 0\right)}{{\lambda }_{0}}, {G}_{0}={\lambda }_{0}S\left(\rho \right), \dfrac{\text{d}\rho }{\text{d}\xi }=P\left(\rho \right) $ 和相应的内变量$ {\rho }_{\text{*}}=\dfrac{\rho -{\rho }_{\mathrm{c}}}{{\varepsilon }^{\alpha }} $ , 得到转化后的Gibbs-Thomson条件:$ \begin{split}\text{i}\dfrac{\partial \widetilde{{C}_{*0}}}{\partial {\zeta }_{*}}=\;&\text{i}\dfrac{\partial }{\partial {\zeta }_{*}} \bigg\{-\widehat{P}eW\left[{\lambda }_{G}-\left({y}_{\text{*0}}-1\right)\right]\widetilde{{h}_{*0}} \\ & +\dfrac{{\varepsilon }^{1-2\alpha }}{MW{G}_{0}}\dfrac{{\partial }^{2}\widetilde{{h}_{*0}}}{\partial {\mathrm{\zeta }}_{*}^{2}}\bigg\}. \end{split} $ 以及转化后的质量守恒条件:
$ \begin{split}&{\varepsilon }^{1-2\alpha }{P}^{3}\left(\rho \right)\dfrac{{\partial }^{3}\widetilde{{h}_{*0}}}{\partial {\rho }_{*}^{3}}+\overline{{\varLambda }_{1}}{\lambda }_{0}^{2}S\left(\rho \right)P\left(\rho \right)\left(1-\text{i}\rho \right)\\ &\times\dfrac{\partial \widetilde{{h}_{*0}}}{\partial {\rho }_{*}} -\text{i}{\varepsilon }^{\alpha -\tfrac{1}{2}}{W}^{2}M\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{\sigma }_{0}{\lambda }_{0}^{3}\\ &\times{S}^{3}\left(\rho \right)\widetilde{{h}_{*0}}+\left(h.o.t\right)=0.\end{split} $ 为了求解(52)式, 对外部区域和内部区域对的解分别运用变换
$\widetilde{{h}_{0}}\left(\rho \right)=\widetilde{{W}_{0}}\left(\rho \right)\mathrm{exp}\left\{\dfrac{\text{i}}{\sqrt{\mathrm{\varepsilon }}}{\displaystyle\int }_{{\rho }_{\mathrm{c}}}^{\rho }{k}_{\mathrm{c}}\left({\rho }_{1}\right)\text{d}{\rho }_{1}\right\}$ 和$\widetilde{{h}_{*0}}\left({\mathrm{\rho }}_{*}\right)=\widetilde{{W}_{*0}}\left({\rho }_{*}\right)\mathrm{exp}\left\{\dfrac{\text{i}}{\sqrt{\varepsilon }}{\displaystyle\int }_{{\rho }_{\mathrm{c}}}^{\rho }{k}_{\mathrm{c}}\left({\rho }_{1}\right)\text{d}{\rho }_{1}\right\}$ , 参照波函数$ {k}_{\mathrm{c}}\left(\rho \right) $ 待定, 且满足$ \text{Re}\left\{{k}_{0}^{\left(3\right)}\right\} < \text{Re}\left\{{k}_{\mathrm{c}}\right\} < \text{Re}\left\{{k}_{0}^{\left(1\right)}\right\} $ . 于是外部区域的解$ \widetilde{{h}_{0}} $ 可写作两个$ W $ 波的组合:$ \begin{split}\widetilde{{W}_{0}}\left(\rho \right)={D}_{1}\widetilde{{W}_{0}^{\left(+\right)}}\left(\rho \right)+{D}_{3}\widetilde{{W}_{0}^{\left(-\right)}}\left(\rho \right),\end{split} $ 其中:
$\begin{split} \widetilde{{W}_{0}^{\left(+\right)}}\left(\rho \right)&={H}_{1}\left(\rho \right)\mathrm{exp}\left\{-\dfrac{\text{i}}{\sqrt{\mathrm{\varepsilon }}}\int _{{\rho }_{\mathrm{c}}}^{\rho }{k}_{\mathrm{c}}\left(\rho \right)\text{d}{\rho }_{1}\right\},\\ \widetilde{{W}_{0}^{\left(-\right)}}\left(\rho \right)&={H}_{3}\left(\rho \right)\mathrm{exp}\left\{-\dfrac{\text{i}}{\sqrt{\mathrm{\varepsilon }}} \int _{{\rho }_{\mathrm{c}}}^{\rho }{k}_{\mathrm{c}}\left({\rho }_{1}\right)\text{d}{\rho }_{1}\right\}. \end{split} $ 此时, 可把(52)式重写成以下形式的控制方程:
$ \begin{split}&\;{\varepsilon }^{1-2\alpha }{\varOmega }_{3}\left(\rho \right)\dfrac{{\partial }^{3}\widetilde{{W}_{*0}}\left({\rho }_{*}\right)}{\partial {\rho }_{*}^{3}}+{\varepsilon }^{1/2-\alpha }{\varOmega }_{2}\left(\rho \right)\dfrac{{\partial }^{2}\widetilde{{W}_{*0}}\left({\rho }_{*}\right)}{\partial {\rho }_{*}^{2}}\\ &+{\varOmega }_{1}\left(\rho \right)\dfrac{\partial \widetilde{{W}_{*0}}\left({\rho }_{*}\right)}{\partial {\rho }_{*}} +{\varOmega }_{4}\left(\rho \right)\widetilde{{W}_{*0}}\left({\rho }_{*}\right)\\ &-\text{i}{\varepsilon }^{\alpha -1/2}{W}^{2}M\widehat{P}e\left(1-\kappa \right){y}_{\text{*0}}{\sigma }_{0}{\lambda }_{0}^{3}{S}^{3}\left(\rho \right)\widetilde{{W}_{*0}}\left({\rho }_{*}\right) \\ &+\left(h.o.t\right)=0,\\[-10pt]\end{split} $ 其中:
$ \begin{split} {\varOmega }_{0}\left(\rho \right)=\;&\varSigma \left({k}_{\mathrm{c}},\zeta \right)=\dfrac{{k}_{\mathrm{c}}\left(\rho \right)P\left(\rho \right)}{\overline{{\varLambda }_{0}}{\lambda }_{0}{S}^{2}\left(\rho \right)}\\ &\times\left[-\dfrac{{k}_{\mathrm{c}}^{2}\left(\rho \right){P}^{2}\left(\rho \right)}{\overline{{\varLambda }_{1}}{\lambda }_{0}^{2}S\left(\rho \right)}+\left(1-\text{i}\rho \right)\right],\\ {\varOmega }_{1}\left(\rho \right) =\;&-3{k}_{\mathrm{c}}^{2}{\varOmega }_{3}\left(\rho \right)+\overline{{\varLambda }_{1}}{\lambda }_{0}^{2}S\left(\rho \right)P\left(\rho \right)\left(1-\text{i}\rho \right),\\ {\varOmega }_{2}\left(\rho \right)=\;&3\text{i}{k}_{\mathrm{c}}{\varOmega }_{3}\left(\rho \right),\;{\varOmega }_{3}\left(\rho \right)={P}^{3}\left(\rho \right), \\ {\varOmega }_{4}\left(\rho \right)=\;&\text{i}{\varepsilon }^{\alpha -1/2} \left[{W}^{2}M\widehat{P}e \left(1-\kappa \right) {y}_{\text{*0}}{\lambda }_{0}^{3}{S}^{3} \left(\rho \right)\right] {\varOmega }_{0} \left(\rho \right) . \end{split} $ 选取
$ {k}_{\mathrm{c}}=\sqrt{\dfrac{\overline{{\varLambda }_{1}}{\lambda }_{0}^{2}S\left(\rho \right)\left(1-\text{i}\rho \right)}{3{P}^{2}\left(\rho \right)}} $ 可得$ {\varOmega }_{1}\left(\rho \right)=0 $ , 则(54)式最终化为$ \begin{split}&{\varepsilon }^{1-2\alpha }{P}^{3}\left(\rho \right)\dfrac{{\partial }^{3}\widetilde{{W}_{*0}}\left({\rho }_{*}\right)}{\partial {\rho }_{*}^{3}}+{\varepsilon }^{1/2-\alpha }\text{i}{\lambda }_{0}{P}^{2}\left(\rho \right)\\ &\times\sqrt{3\overline{{\varLambda }_{1}}S\left(\rho \right)\left(1-\text{i}\rho \right)}\dfrac{{\partial }^{2}\widetilde{{W}_{*0}}\left({\rho }_{\text{*}}\right)}{\partial {\rho }_{*}^{2}} \\ &\times \left[{\sigma }_{0}-\dfrac{2}{\sqrt{27}}\dfrac{\sqrt{\overline{{\varLambda }_{1}}}}{\overline{{\varLambda }_{0}}}\dfrac{{\left(1-\text{i}\rho \right)}^{2/3}}{{S}^{2/3}\left(\rho \right)}\right]\\ &\times{\lambda }_{0}^{3}{S}^{3}\left(\rho \right)\widetilde{{W}_{*0}}\left({\rho }_{*}\right)+\left(h.o.t\right)=0.\end{split} $ (55)式有5个孤立奇点和转向点:
$ \rho =\pm \text{i}, \pm \text{i}\alpha , {\rho }_{\mathrm{c}} $ , 其中$ {\rho }_{\mathrm{c}} $ 是方程中复平面$ \rho $ 内的一个简单转向点,$ \rho =\pm \text{i}, \pm \text{i}\alpha $ 分别是函数$ S\left(\rho \right) $ 和$ P\left(\rho \right) $ 的零点. 由于:$ \begin{split}{\sigma }_{0}=\dfrac{2}{\sqrt{27}}\dfrac{\sqrt{\overline{{\varLambda }_{1}}}}{\overline{{\varLambda }_{0}}}{\left(\dfrac{1-\text{i}{\rho }_{\mathrm{c}}}{1+\text{i}{\rho }_{\mathrm{c}}}\right)}^{3/4},\end{split} $ 因此, 要研究转向点
$ {\rho }_{\mathrm{c}} $ 附近内解行为以得出一致有效渐近解, 需要考虑以下两种情况: 1)$ \left|{\sigma }_{0}\right|=O\left(1\right) $ ; 2)$ \left|{\sigma }_{0}\right|\ll 1 $ . 情况1)可得如下的连接条件:$ \begin{split}{H}^{\left(2\right)}=\;&v\left(z{\mathrm{e}}^{\text{i}\mathrm{\pi }}\right)-2\mathrm{cos}\left(v\mathrm{\pi }\right){H}_{v}^{\left(2\right)}\left(z\right)+{\mathrm{e}}^{\text{i}v\mathrm{\pi }}{H}_{v}^{\left(1\right)}\left(z\right) \\ =\;&2\mathrm{cos}\left(v\mathrm{\pi }\right)\sqrt{\dfrac{2}{\mathrm{\pi }z}}{\mathrm{e}}^{-\text{i}z+\text{i}\left(v/2+1/4\right)\mathrm{\pi }}\\ &+{\mathrm{e}}^{\text{i}v\mathrm{\pi }\sqrt{\tfrac{2}{\mathrm{\pi }z}}}{\mathrm{e}}^{\text{i}z-\text{i}\left(v/2+1/4\right)\mathrm{\pi }}\\ =\;&{\mathrm{e}}^{\text{i}\left(1/6+1/4\right)\mathrm{\pi }\sqrt{\tfrac{2}{\mathrm{\pi }z}}}{\mathrm{e}}^{-\text{i}z}-\text{i}{\mathrm{e}}^{\text{i}\left(1/6+1/4\right)\mathrm{\pi }\sqrt{\tfrac{2}{\mathrm{\pi }z}}}{\mathrm{e}}^{\text{i}z}\\ =\;&{D}_{3}{\mathrm{e}}^{-\text{i}z}+{D}_{1}{\mathrm{e}}^{\text{i}z}.\\[-11pt] \end{split} $ 则
${{D}_{1}}/{{D}_{3}}=-\text{i}={\mathrm{e}}^{-\tfrac{1}{2}\mathrm{\pi }\text{i}}, {D}_{3}={D}_{3}',$ 其中$ {H}_{v}^{\left(2\right)}\left(z\right) $ 是第二类$ v $ 阶Hankel函数. 情况2)又包含两种情况: 一个是奇异点$ \rho =-\text{i} $ 位于$ {\rho }_{\mathrm{c}} $ 附近的内部区域, 但$ \rho =-\text{i}a $ 不在; 另一种则是两个奇异点都在$ {\rho }_{\mathrm{c}} $ 附近的内部区域. 前一种情况下, 可得以下的连接条件:$ \begin{split} {{D}_{1}}/{{D}_{3}}&=-\text{i}2\mathrm{cos}\left(v\mathrm{\pi }\right)=2\mathrm{cos}\left(v\mathrm{\pi }\right){\mathrm{e}}^{-\tfrac{1}{2}\mathrm{\pi }\text{i}},\\ {D}_{3}&={D}_{3}':\rho \in {S}_{1};\rho \in \left(0,{\rho }_{\mathrm{c}}\right), \; {{D}_{1}}/{{D}_{3}}=0,\\ {D}_{3}&={D}_{3}':\rho \in {S}_{2}'\cup {S}_{2};\rho \in \left({\rho }_{\mathrm{c}}',\mathrm{\infty }\right). \end{split} $ 后一种情况则无法与外解匹配, 故排除.
-
内部区域远离远场的内部方程可写成如下的Airy方程:
$ \begin{split}\dfrac{{\partial }^{2}\widetilde{{W}_{*0}}\left(\widehat{{\rho }_{*}}\right)}{\partial \widehat{{\rho }_{*}^{2}}}+\widehat{{\rho }_{*}^{{p}_{0}}\widetilde{{W}_{*0}}}\left(\widehat{{\rho }_{*}}\right)=0.\end{split} $ 且远场处内解的首级近似具有
$\widetilde{{W}_{*0}}\left(\widehat{{\rho }_{*}}\right)= {D}_{\text{*}}\widehat{{\rho }_{*}^{1/2}}$ ${H}_{v}^{\left(2\right)}\left(z\right)$ 的形式, 其中$z = 2 v\widehat{{\rho }_{*}^{1/\left(2 v\right)}}, v = {1}/({{p}_{0} + 2})$ . 对于情况1, 有$\widehat{{\rho }_{*}}={A}^{\textstyle\frac{1}{3}}{\rho }_{*}, A=O\left(1\right), {p}_{0}=1, {\theta }_{\mathrm{L}}=\dfrac{2}{3}\mathrm{\pi }, \alpha = {1}/{3}, v= {1}/{3}$ ; 对于情况2, 则有$ \widehat{{\rho }_{*}}={A}_{\text{*}}^{4/15}{\rho }_{*}, {A}_{\text{*}}= O\left(1\right), {p}_{0}=\dfrac{7}{4}, {\theta }_{\mathrm{L}}=\dfrac{8}{15}\mathrm{\pi }, \alpha =\dfrac{2}{7}, v=\dfrac{4}{15} $ . 参数$ {\theta }_{\mathrm{L}} $ 表示两条Stokes线的夹角. 通过匹配内解和外解, 最终得到两种情况下的统一形式的连接条件:$ 1)~ {{D}_{1}}/{{D}_{3}} = -\text{i}2\cos(v\mathrm{\pi }) = 2\cos(v\mathrm{\pi }){\mathrm{e}}^{-\tfrac{1}{2}\mathrm{\pi }\text{i}},\;{D}_{3} = {D}_{3}', $ $ 2)~ {{D}_{1}}/{{D}_{3}}=0,~~{D}_{3}={D}_{3}'. $ 在这基础上运用尖端光滑条件后, 复特征值
$ {\mathrm{\sigma }}_{0} $ 可以确定$ \varepsilon $ 和其他参数. -
对于4.4节的情况1,
$ {p}_{0}=1 $ ,$v= {1}/{3}$ . 假设$ {\sigma }_{0}= {\sigma }_{\mathrm{R}}-\text{i}\omega \left(\omega > 0\right) $ , 只考虑生长速度较小的模式, 即$ \left|{\sigma }_{\mathrm{R}}\ll 1\right| $ 进行稳定性分析. 在外部区域使用复特征值$ {\sigma }_{0} $ 表示物理解:$ \text{Re}\left\{\widetilde{{h}_{0}}\left(\rho ,t\right)\right\}=\text{Re}\left\{H\left(\rho \right){\mathrm{e}}^{\tfrac{{\mathrm{\sigma }}_{0}t}{\sqrt{\mathrm{\varepsilon }}}}\right\}, $ 其中
$ H\left(\rho \right)={D}_{1}{H}_{1}+{D}_{3}{H}_{3} $ ,$ {D}_{1}, {D}_{3} $ 是$ H $ 波的系数,$ {H}_{1}, {H}_{3} $ 是$ H $ 波, 且有:$ {d}_{1}={D}_{1}{\mathrm{e}}^{-\text{i}{\mathrm{\chi }}_{1}},{d}_{3}={D}_{3}{\mathrm{e}}^{-\text{i}{\chi }_{3}}, $ 其中
$ {\chi }_{1}=\dfrac{1}{\sqrt{\mathrm{\varepsilon }}}{\displaystyle\int }_{0}^{{\rho }_{\mathrm{c}}}\widetilde{{k}_{0}^{\left(1\right)}}\mathrm{d}\rho , {\chi }_{3}=\dfrac{1}{\sqrt{\varepsilon }}{\displaystyle\int }_{0}^{{\rho }_{\mathrm{c}}}\widetilde{{k}_{0}^{\left(3\right)}}\mathrm{d}\rho $ .然后根据(59)式, 则有:
$ \dfrac{{d}_{1}}{{d}_{3}}=\dfrac{{D}_{1}}{{D}_{3}}=-\text{i}{\mathrm{e}}^{-\text{i}\left({\chi }_{1}-{\chi }_{3}\right)}=-\text{i}{\mathrm{e}}^{-\text{i}\chi }, $ 其中
$\chi =\dfrac{1}{\sqrt{\mathrm{\varepsilon }}} \displaystyle\int_{0}^{{\rho }_{\mathrm{c}}}\left(\widetilde{{k}_{0}^{\left(1\right)}}-\widetilde{{k}_{0}^{\left(3\right)}}\right)\text{d}\text{ρ}$ .由尖端光滑性条件,
$ {d}_{1} $ 和$ {d}_{3} $ 要满足:1) 对称S-模式:
$ \begin{split}\dfrac{{d}_{3}}{{d}_{1}}=-\dfrac{\widetilde{{k}_{0}^{\left(1\right)}}\left(0\right)}{\widetilde{{k}_{0}^{\left(3\right)}}\left(0\right)};\end{split} $ 2)反对称A-模式:
$ \begin{split}{d}_{1}=-{d}_{3}. \end{split} $ $ \begin{split}&\dfrac{1}{{\mathrm{\varepsilon }}_{e}}\int_{0}^{{\rho }_{\mathrm{c}}}\Big(\widehat{{k}_{0}^{\left(1\right)}}-\widehat{{k}_{0}^{\left(3\right)}}\Big)\text{d}\rho \\ =\;&\left(2n+1+\dfrac{1}{2}+{\theta }_{0}\right)\pi -\text{i}\mathrm{ln}{\alpha }_{0},\\ & n=0,\pm 1,\pm 2,\cdots ,\end{split} $ 其中
$\widehat{{k}_{0}^{\left(i\right)}}\left(\rho \right)=\dfrac{{k}_{\mathrm{e}}^{\left(i\right)}\left(\rho \right)}{G\left(\rho \right)}=\dfrac{\widetilde{{k}_{0}^{\left(i\right)}}\left(\rho \right)}{{\mathrm{\lambda }}_{0}\sqrt{{\varLambda }_{1}}}$ ;$ {\varepsilon }_{\mathrm{e}}=\dfrac{1}{{\lambda }_{0}}\sqrt{\dfrac{\varepsilon }{{\varLambda }_{1}}} $ .S-模式下
$ {\alpha }_{0}{\mathrm{e}}^{\text{i}{\theta }_{0}\mathrm{\pi }}=\dfrac{\widetilde{{k}_{0}^{\left(1\right)}}\left(0\right)}{\widetilde{{k}_{0}^{\left(3\right)}}\left(0\right)} $ , A-模式下$ {\alpha }_{0}=1, {\theta }_{0}={y}_{\text{*0}}=\dfrac{1+{\lambda }_{G}\left(1-{\lambda }_{0}\right)}{1-{\lambda }_{0}\left(1-\kappa \right)} $ , 因此当前系统的参数$ \overline{{\varLambda }_{1}}=M{W}^{2}\widehat{P}e\left[\left(1-\kappa \right){y}_{\text{*0}}-{\lambda }_{G}\right]{\lambda }_{0} $ 的函数.量子化条件(63)确定了复特征值
$ {\mathrm{\sigma }}_{0}\left(\left|{\mathrm{\sigma }}_{0}\right|= O\left(1\right)\right) $ 的频谱:$ \left\{{\mathrm{\sigma }}_{0, n}\right\}, n=\mathrm{0, 1}, 2, $ 它们是胞晶相对宽度$ {\mathrm{\lambda }}_{0} $ 和小参数$ \mathrm{\varepsilon } $ 的参数. 这个频谱产生了两个离散的特征模式列: S-模式和A-模式. 给定$ {\mathrm{\lambda }}_{0} $ ,$ \widehat{P}e $ 和其他物理参数, 系统允许一组中性稳定模式$ {\mathrm{\sigma }}_{R}=0 $ , 此时$ \mathrm{\varepsilon }={\mathrm{\varepsilon }}_{\text{*}n}, n=\mathrm{0, 1}, 2 $ , 且$ {\varepsilon }_{\text{*}}={\varepsilon }_{\text{*0}} > {\varepsilon }_{\text{*1}} > {\varepsilon }_{\text{*2}} $ , 它们表示沿着界面传播的行波, 因此也称作整体振荡不稳定为整体行波机制. 在首级近似下, 可以使用$ R\left\{{\sigma }_{0}\right\}=0 $ 来计算$ {\varepsilon }_{\text{*}} $ 取值, 一级近似下使用$ R\left\{{\mathrm{\sigma }}_{0}+\varepsilon {\mathrm{\sigma }}_{1}\right\}=0 $ . 为了方便计算, 使用新的操作数:$ {\varepsilon }_{\mathrm{c}}=\sqrt{\dfrac{{l}_{\mathrm{c}}V}{{\kappa }_{\mathrm{D}}}},{\lambda }_{G}=\dfrac{{G}_{\mathrm{c}}}{{\varepsilon }_{\mathrm{c}}^{2}},\overline{{\varLambda }_{1}}=\widehat{Pe}\widehat{{\varLambda }_{1}}, $ 其中:
$ \begin{split} {G}_{\mathrm{c}}&=\dfrac{{l}_{\mathrm{c}}}{{l}_{G}},\widehat{{\varLambda }_{1}}=M{W}^{2}\left[\left(1-\kappa \right){y}_{\text{*0}}-\dfrac{{G}_{\mathrm{c}}}{{\varepsilon }_{\mathrm{c}}^{2}}\right],\\ \widehat{P}e&=\dfrac{{\varepsilon }_{\mathrm{c}}^{2}}{{\varepsilon }^{3}},{\varepsilon }_{\mathrm{e}}=\dfrac{{\varepsilon }^{2}}{{\lambda }_{0}\sqrt{\widehat{{\varLambda }_{1}}}{\varepsilon }_{\mathrm{c}}}. \end{split} $ 由(24), (56), (63)式, 发现对于同一个
$ n $ , GTW-S模式增长率比GTW-A模式更大, 也称GTW-S模式比GTW-A模式更危险. 此外还可以得到$ {\varepsilon }_{\text{*}} $ 和$ {\mathrm{\lambda }}_{0} $ 的关系, 并得到不同的物理参数下$ {\varepsilon }_{\text{*}} $ 和$ {\lambda }_{0} $ 的图像, 得到界面动力学参数$ {M}_{\text{*}} $ 对系统稳定区域大小的影响.通过绘图发现, 一级近似下, 界面动力学参数
$ {M}_{\text{*}} $ 越大, 系统的稳定区域越大. 图2展示了首级近似和一级近似下$ {\varepsilon }_{\text{*}} $ 和$ {\lambda }_{0} $ 的关系. 图像表示, 对于同一个胞晶相对宽度$ {\lambda }_{0} $ , 一级近似下的$ {\varepsilon }_{\text{*}} $ 小于首级近似下的$ {\varepsilon }_{\text{*}} $ . 图3展示了$ n=\mathrm{0, 1}, 2 $ 时的GTW-S中性曲线, 发现GTW机制下$ n=0 $ 时最危险. 图4和5分别展示了$ E=\mathrm{0.1, 0.25} $ 时和$ {m}_{\text{*}}=\mathrm{1, 5}, 10 $ 时的GTW-S中性曲线. 发现对于同一个$ {\mathrm{\lambda }}_{0} $ ,$ E $ 越小, 系统的稳定区域越大, 或$ {m}_{\text{*}} $ 越大, 系统稳定区域越大. 这里$ {m}_{\text{*}} $ 是一个与界面动力学参数$ {M}_{\text{*}} $ 有关的参数, 有$ {M}_{\text{*}}={\varepsilon }^{2}{m}_{\text{*}} $ ;$ E=\dfrac{{\Delta}H}{{c}_{\mathrm{p}}\rho {T}_{M}} $ 是一个和纯熔体温度$ {T}_{M} $ 相关的参数.
图 2 首级近似与一级近似的GTW-S中性模式曲线. 参数分别为
$ n=0 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ Figure 2. The neutral curves of GTW-S-modes with zero-th-order approximation and first-order approximation for the case
$ n=0 $ ,$ {\lambda }_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,${m}_{\text{*}}=1$ 
图 3 一级近似下的GTW-S中性模式曲线. 参数分别为
$ n=0, 1, 2 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ Figure 3. The neutral curves of GTW-S-modes with first-order approximation for the case
$ n=\mathrm{0, 1}, 2 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M= $ $ 0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ .
图 4 一级近似下的GTW-S中性模式曲线. 参数分别为
$ E = 0.1, 0.25 $ ,$ n = 0 $ ,$ {\mathrm{\lambda }}_{G} = 0.3991 $ ,$ \kappa = 0.29 $ ,$ {G}_{\mathrm{c}} = 0.14485\times $ $ {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ {m}_{\text{*}}=1 $ Figure 4. The neutral curves of GTW-S-modes with first-order approximation for the case of
$ E=0.1, 0.25 $ ,$ n=0 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${{\varepsilon }}_{\mathrm{c}}=0.5388\times $ $ {10}^{-2}$ ,$ M=0.09552 $ ,${m}_{\text{*}}=1$ 
图 5 一级近似下的GTW-S中性模式曲线. 参数分别为
$ {m}_{\text{*}}=1, 5, 10 $ ,$ E=0.25 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}= $ $ 0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ Figure 5. The neutral curves of GTW-S-modes with first-order approximation for the case of
$ {m}_{\text{*}}=1, 5, 10 $ ,$ E=0.25 $ ,$ n=0 $ ,$ {\lambda }_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}= $ $ 0.5388\times {10}^{-2}$ ,$M=0.09552$ 从以上分析发现, GTW-S中性模式的曲线将平面分成了稳定区域(S)和不稳定区域(Os.U). 由此得到振荡稳定性判断依据: 若
$ \left(\varepsilon , {\lambda }_{0}\right)\in \left(\mathrm{S}\right) $ , 则稳定; 若$\left(\varepsilon , {\lambda }_{0}\right)\in \left(\mathrm{O}\mathrm{s}. \mathrm{U}\right)$ , 则振荡不稳定.对于4.4节的情况2, 这种情况导致实特征值
$ \left(\left|{\sigma }_{0}\right|\ll 1\right) $ 的频谱. 此时系统此时系统允许两种整体低频模式, 包括对称模式与反对称模式. 但是在该模式的首级近似下, 界面动力学参数不起作用, 不影响系统在该模式下的稳定性. 一阶近似下界面动力学会影响稳定性, 后续会跟进研究. -
本文通过匹配渐近展开法和多重变量展开法, 研究了定向凝固过程中界面动力学参数对深胞晶界面形态的稳定性造成的影响. 通过定义快变量进行变量替换, 寻找外部系统和根部系统的模式解, 导出了胞晶界面扰动振幅的变化率满足的色散关系, 得到了整体模式解, 界面形态的量子化条件, 内解与外解的匹配条件以及深胞晶生长的临界稳定性判断依据. 结果表明, 界面动力学参数对定向凝固中对整体波动不稳定性有影响. 考虑了界面动力学的胞晶拥有两种整体不稳定性机制: 整体振荡不稳定性和整体低频不稳定性. 整体振荡不稳定性出现在复特征值频谱的情况下, 表示沿着界面传播的行波, 此时系统允许对称S-模式和反对称A-模式. 而整体低频不稳定性出现在实特征值频谱的情况下, 此时系统允许允许对称模式和反对称模式. 稳定性分析表明, 在整体波动不稳定性中, GTW-S模式
$ n=0 $ 是最危险的模式, 其整体振荡模式中的枝晶结构的不稳定区域最大. 在其他参数固定的情况下, 界面动力学参数$ {M}_{\text{*}} $ 越大, 则系统越稳定, 整体振荡模式中的枝晶结构的整体波动不稳定性的稳定区域越大.
-
研究界面动力学对定向凝固中深胞晶形态稳定性的影响. 应用多重变量法和匹配渐近法, 通过寻找系统的模式解, 导出了胞晶界面扰动振幅的变化率满足的色散关系, 得到了界面形态的量子化条件. 结果表明, 考虑了界面动力学参数的深胞晶生长的定向凝固系统有两种整体不稳定性机制, 整体振荡不稳定机制和低频不稳定性. 稳定性分析表明, 界面稳定性参数
$\varepsilon$ 与胞晶相对参数$ {\lambda }_{0} $ 有关, 低阶时界面动力学参数$ {M}_{\text{*}} $ 越大, 中性模式产生强振荡的枝晶结构的整体波动不稳定性的稳定区域越大.The effect of interface kinetics on the stability of deep cell morphology in directional solidification is studied. By using the multiple variable method and the matching asymptotic methodandby finding the mode solution of the system,the dispersion relation satisfied by the change rate of the disturbance amplitude of the cell-crystal interface is derived , and the quantization condition of the interface morphology is obtained. The results show that there are two global instability mechanisms in the directional solidification system with considering the growth of deep cell crystal with interfacial dynamic parameters : global oscillation instability mechanism and low-frequency instability. The stability analysis shows that the interface stability parameter$\mathrm{\varepsilon }$ is related to the cell relative parameter$ {\mathrm{\lambda }}_{0} $ , and thatthe larger the interface dynamic parameter$ {M}_{\text{*}} $ , the larger the stable region of the overall fluctuation instability of the dendrite structure in the overall oscillation modeis.-
Keywords:
- directional solidification /
- deep cellular crystal growth /
- interface kinetics /
- morphological stability
[1] Peng P, Li S Y, Zheng W C, Lu L, Zhou S D 2021 Trans. Nonferrous Met. Soc. China 31 3096
Google Scholar
[2] Mullins W W, Sekerka R F 1963 Appl. Phys. 34 323
Google Scholar
[3] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp345–352
[4] Nash G E, Glicksman M E 1974 ScriptaMetal. 8 xxix
Google Scholar
[5] KruskalMD, Segur H 1991 Stud. Appl. Math. 85 129
Google Scholar
[6] Xu J J 1991 Phys. Rev. A. 43 930
Google Scholar
[7] Xu J J 1991 Eur. J. Appl. Math. 2 105
Google Scholar
[8] Pocheau A, Georgelin M 1999 J. Cryst. Growth 206 215
Google Scholar
[9] Ding G, Huang W, Xin L, Zhou Y 1997 J. Cryst. Growth 177 281
Google Scholar
[10] Coriell S R, Sekerka R F 1976 J. Cryst. Growth 34 157
Google Scholar
[11] Trivedi R, Seetharaman V, Eshelman M A 1991 Metall. Mater. Trans. A. 22 585
[12] Li J F, Zhou Y H 2005 中国科学: E辑 35 10
Google Scholar
李金富, 周尧和 2005 Science in China(Series E) 35 10
Google Scholar
[13] Tan Y, Wang H 2012 J. Mater. Sci. 47 5308
Google Scholar
[14] 蒋晗, 陈明文, 王涛, 王自东 2017 物理学报 66 10
Google Scholar
Jiang H, Chen M W, Wang T, Wang Z D 2017 Acta Phys. Sin. 66 10
Google Scholar
[15] Chen M W, Wang Z D, Xu J J 2008 Sci. China Ser. E 51 225
Google Scholar
[16] 陈明文, 倪锋, 王艳林, 王自东, 谢建新 2011 物理学报 60 068103
Google Scholar
Chen M W, Ni F, Wang Y L, Wang Z D, Xie J X 2011 Acta Phys. Sin. 60 068103
Google Scholar
[17] 郭洪民, 杨湘杰 2008 中国有色金属学报 18 651
Google Scholar
Guo H M, Yang X J 2008 Chin. J. Nonferrous Met. 18 651
Google Scholar
[18] 统雷雷, 林鑫, 赵力宁, 黄卫东 2009 金属学报 45 737
Google Scholar
Tong L L, Lin X, Zhao L N, Huang W D 2009 ActaMetall. Sin. 45 737
Google Scholar
[19] Pelcé P 1988 Dynamics of Curved Fronts(New York: Academic. Press) pp155–174
[20] Chen Y Q, Xu J J 2011 Phys. Rev. E 83 041601
Google Scholar
[21] Xu J J, Chen Y Q 2011 Phys. Rev. E 83 061605
Google Scholar
-
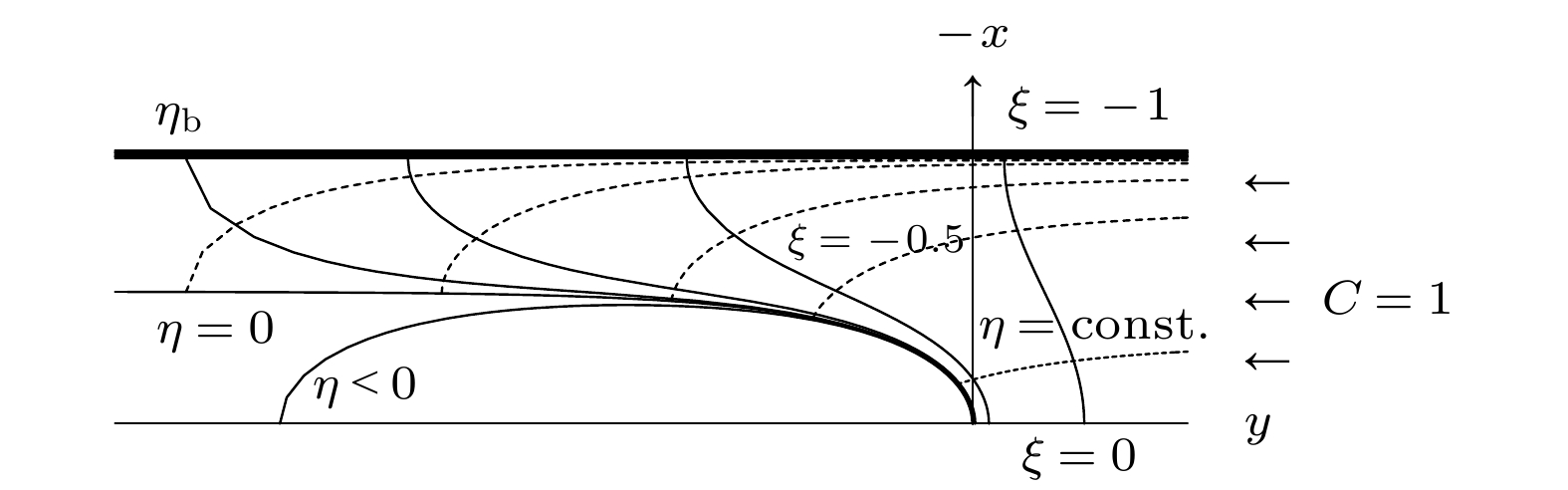
图 1 基于Saffmen-Taylor解构造的曲线坐标系
$ \left(\xi , \eta \right) $ [20]Fig. 1. Curve coordinate system
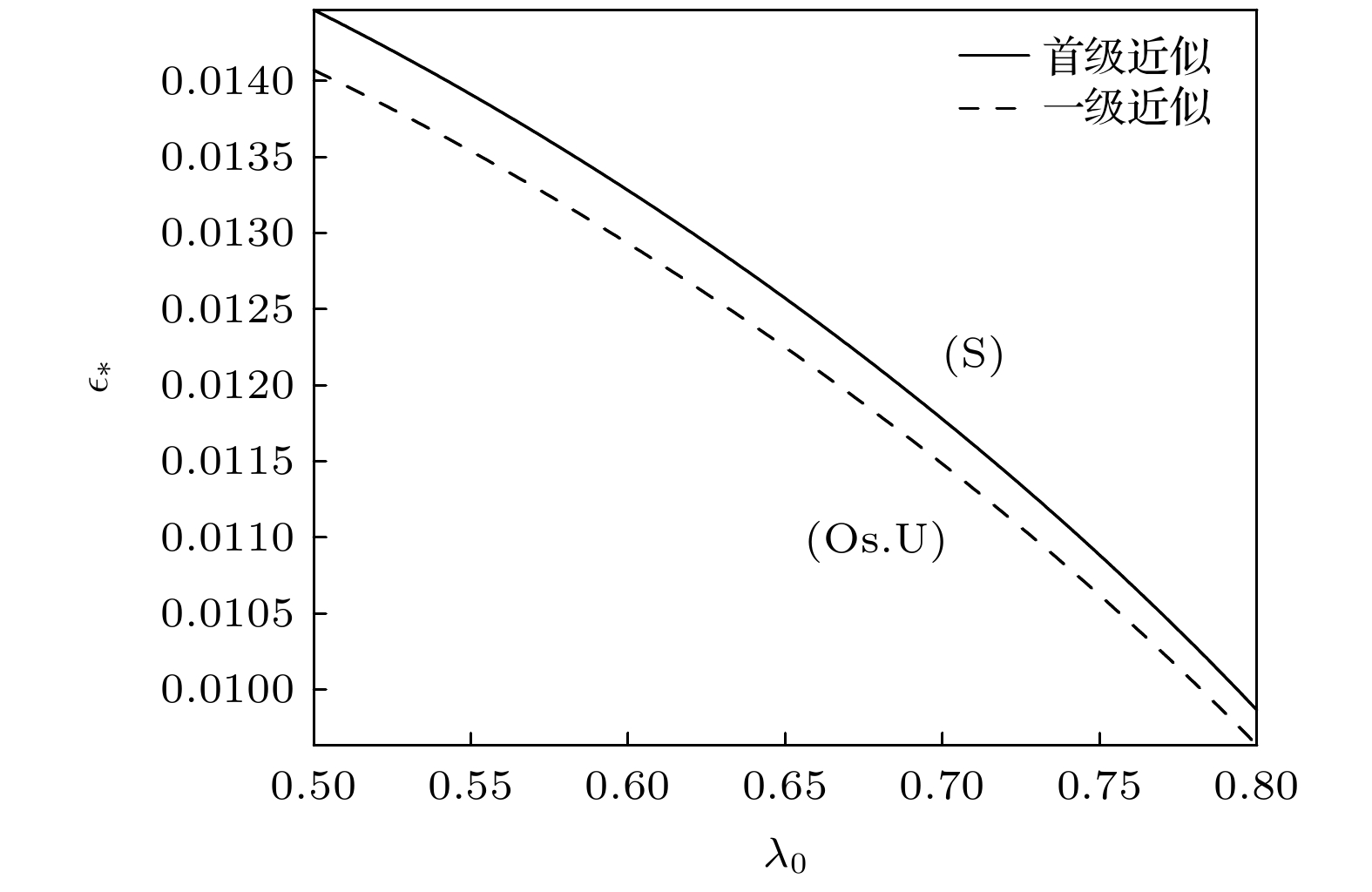
$ \left(\xi , \eta \right) $ based on Saffmen-Taylor solution.
图 2 首级近似与一级近似的GTW-S中性模式曲线. 参数分别为
$ n=0 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ Fig. 2. The neutral curves of GTW-S-modes with zero-th-order approximation and first-order approximation for the case
$ n=0 $ ,$ {\lambda }_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,${m}_{\text{*}}=1$ 
图 3 一级近似下的GTW-S中性模式曲线. 参数分别为
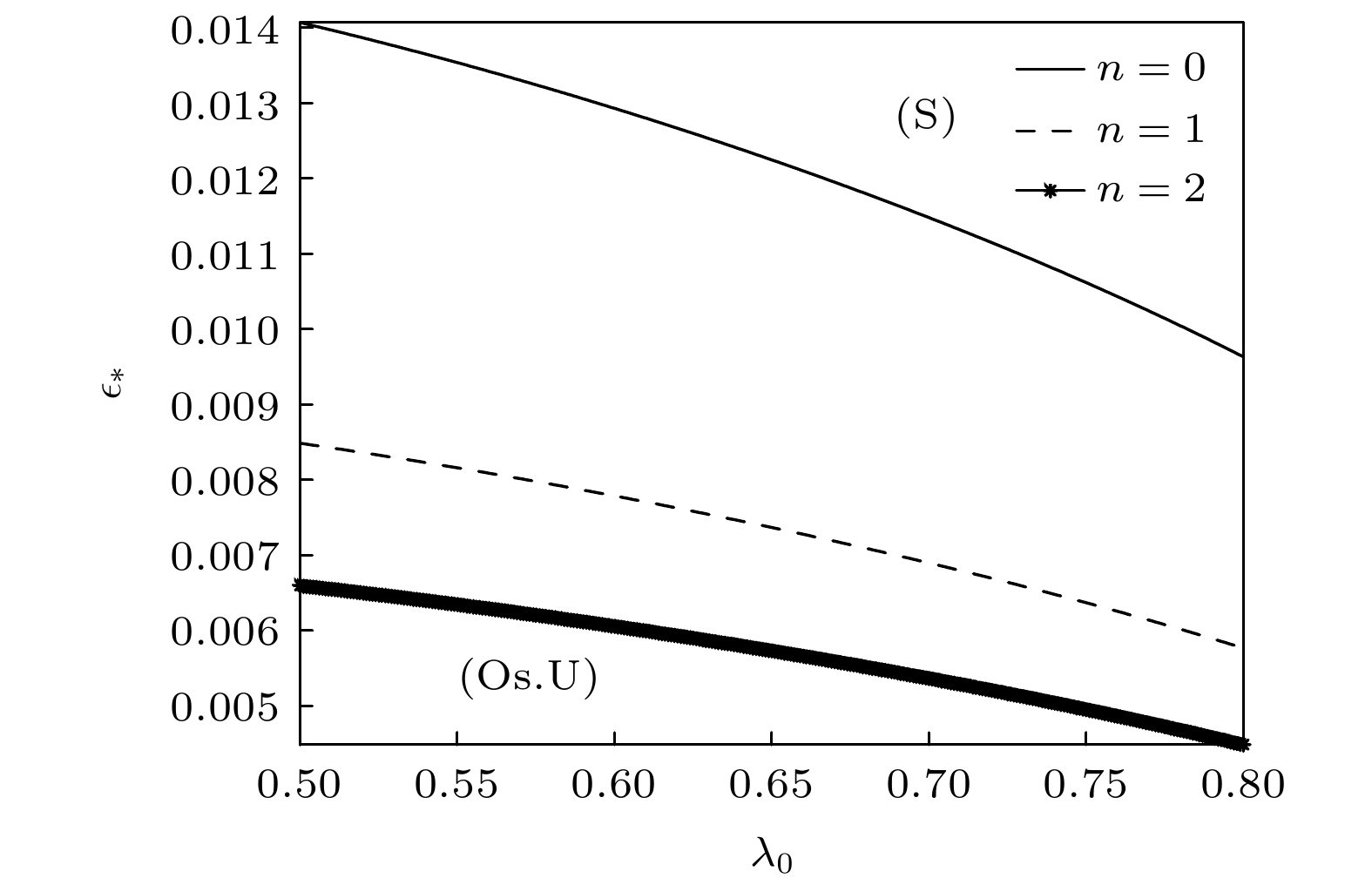
$ n=0, 1, 2 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ Fig. 3. The neutral curves of GTW-S-modes with first-order approximation for the case
$ n=\mathrm{0, 1}, 2 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M= $ $ 0.09552 $ ,$ E=0.25 $ ,$ {m}_{\text{*}}=1 $ .
图 4 一级近似下的GTW-S中性模式曲线. 参数分别为
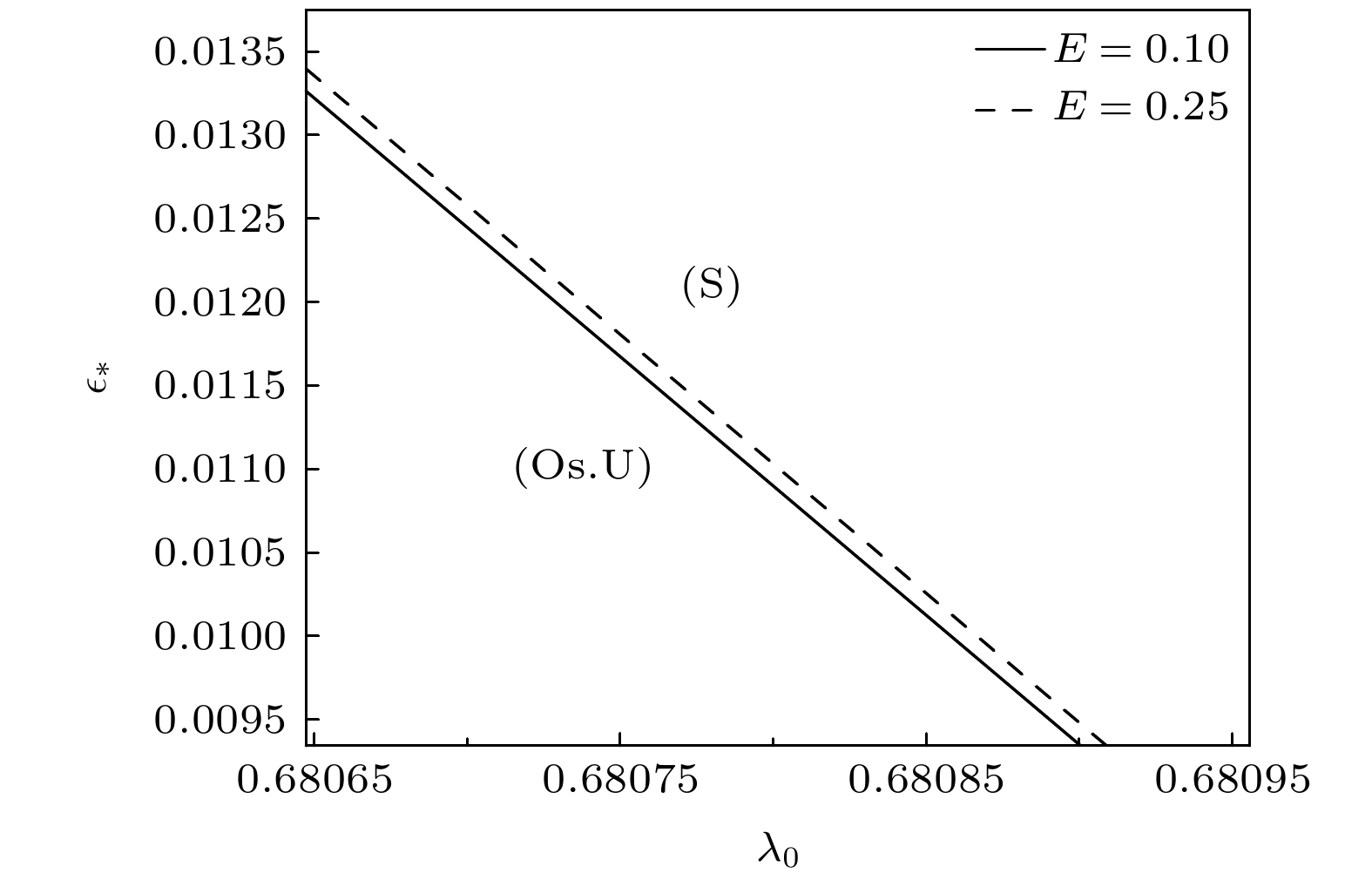
$ E = 0.1, 0.25 $ ,$ n = 0 $ ,$ {\mathrm{\lambda }}_{G} = 0.3991 $ ,$ \kappa = 0.29 $ ,$ {G}_{\mathrm{c}} = 0.14485\times $ $ {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ ,$ {m}_{\text{*}}=1 $ Fig. 4. The neutral curves of GTW-S-modes with first-order approximation for the case of
$ E=0.1, 0.25 $ ,$ n=0 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${{\varepsilon }}_{\mathrm{c}}=0.5388\times $ $ {10}^{-2}$ ,$ M=0.09552 $ ,${m}_{\text{*}}=1$ 
图 5 一级近似下的GTW-S中性模式曲线. 参数分别为
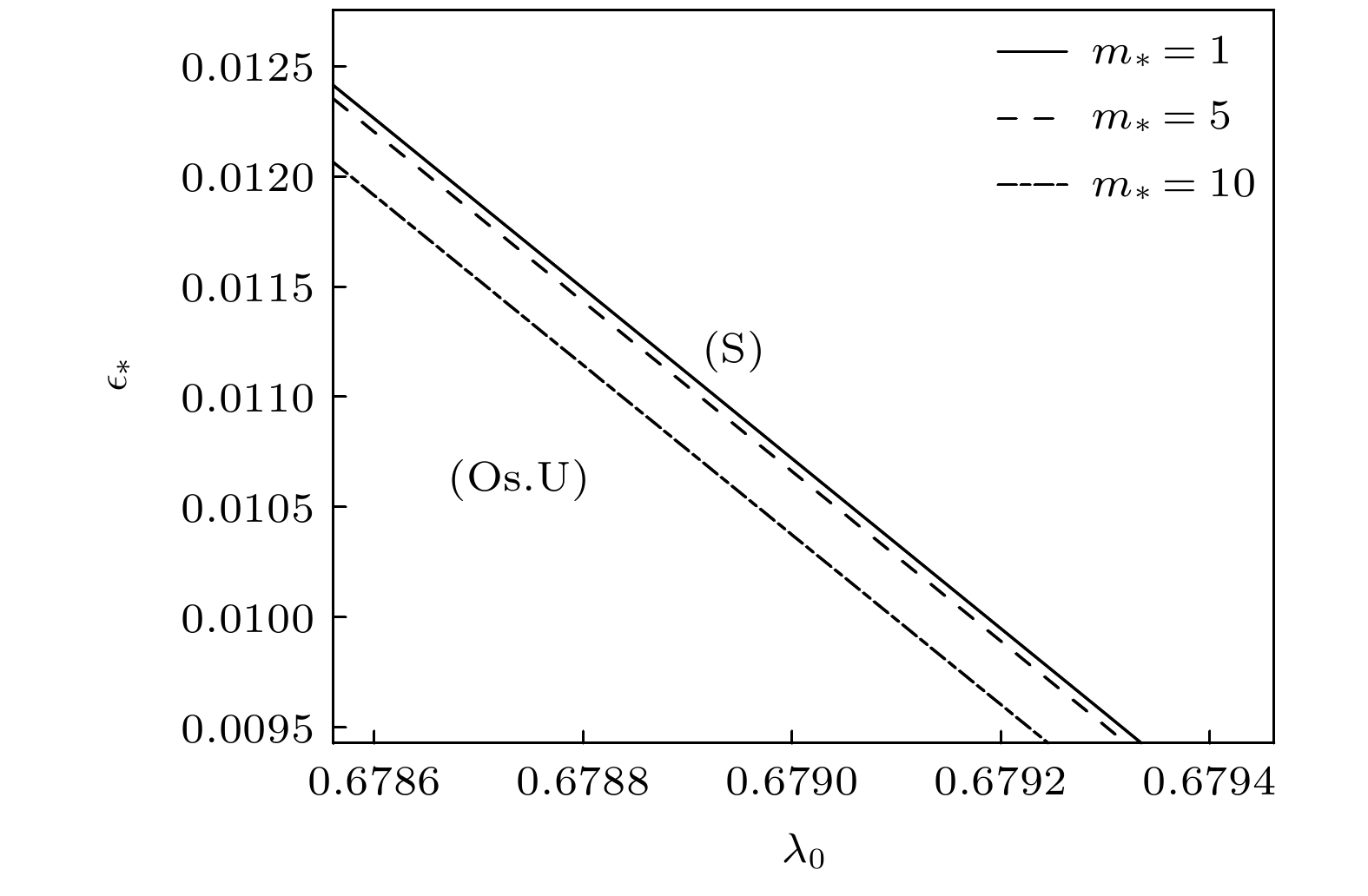
$ {m}_{\text{*}}=1, 5, 10 $ ,$ E=0.25 $ ,$ {\mathrm{\lambda }}_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}= $ $ 0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}=0.5388\times {10}^{-2}$ ,$ M=0.09552 $ Fig. 5. The neutral curves of GTW-S-modes with first-order approximation for the case of
$ {m}_{\text{*}}=1, 5, 10 $ ,$ E=0.25 $ ,$ n=0 $ ,$ {\lambda }_{G}=0.3991 $ ,$ \kappa =0.29 $ ,$ {G}_{\mathrm{c}}=0.14485\times {10}^{-4} $ ,${\varepsilon }_{\mathrm{c}}= $ $ 0.5388\times {10}^{-2}$ ,$M=0.09552$ -
[1] Peng P, Li S Y, Zheng W C, Lu L, Zhou S D 2021 Trans. Nonferrous Met. Soc. China 31 3096
Google Scholar
[2] Mullins W W, Sekerka R F 1963 Appl. Phys. 34 323
Google Scholar
[3] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp345–352
[4] Nash G E, Glicksman M E 1974 ScriptaMetal. 8 xxix
Google Scholar
[5] KruskalMD, Segur H 1991 Stud. Appl. Math. 85 129
Google Scholar
[6] Xu J J 1991 Phys. Rev. A. 43 930
Google Scholar
[7] Xu J J 1991 Eur. J. Appl. Math. 2 105
Google Scholar
[8] Pocheau A, Georgelin M 1999 J. Cryst. Growth 206 215
Google Scholar
[9] Ding G, Huang W, Xin L, Zhou Y 1997 J. Cryst. Growth 177 281
Google Scholar
[10] Coriell S R, Sekerka R F 1976 J. Cryst. Growth 34 157
Google Scholar
[11] Trivedi R, Seetharaman V, Eshelman M A 1991 Metall. Mater. Trans. A. 22 585
[12] Li J F, Zhou Y H 2005 中国科学: E辑 35 10
Google Scholar
李金富, 周尧和 2005 Science in China(Series E) 35 10
Google Scholar
[13] Tan Y, Wang H 2012 J. Mater. Sci. 47 5308
Google Scholar
[14] 蒋晗, 陈明文, 王涛, 王自东 2017 物理学报 66 10
Google Scholar
Jiang H, Chen M W, Wang T, Wang Z D 2017 Acta Phys. Sin. 66 10
Google Scholar
[15] Chen M W, Wang Z D, Xu J J 2008 Sci. China Ser. E 51 225
Google Scholar
[16] 陈明文, 倪锋, 王艳林, 王自东, 谢建新 2011 物理学报 60 068103
Google Scholar
Chen M W, Ni F, Wang Y L, Wang Z D, Xie J X 2011 Acta Phys. Sin. 60 068103
Google Scholar
[17] 郭洪民, 杨湘杰 2008 中国有色金属学报 18 651
Google Scholar
Guo H M, Yang X J 2008 Chin. J. Nonferrous Met. 18 651
Google Scholar
[18] 统雷雷, 林鑫, 赵力宁, 黄卫东 2009 金属学报 45 737
Google Scholar
Tong L L, Lin X, Zhao L N, Huang W D 2009 ActaMetall. Sin. 45 737
Google Scholar
[19] Pelcé P 1988 Dynamics of Curved Fronts(New York: Academic. Press) pp155–174
[20] Chen Y Q, Xu J J 2011 Phys. Rev. E 83 041601
Google Scholar
[21] Xu J J, Chen Y Q 2011 Phys. Rev. E 83 061605
Google Scholar
计量
- 文章访问数: 592
- PDF下载量: 19
- 被引次数: 0
