-
本文对有限Su-Schriefer-Heeger(SSH)晶格的能量本征态和电导问题进行求解, 着重研究了引线-样品的耦合强度对其体态和边缘态电导峰的不同影响. 只有在弱耦合极限下, 电导峰才显示全部体态和边缘态的能量本征值; 随着耦合强度的增大, 全部电导峰都逐渐偏离能量本征值并变宽变低, 其中边缘态的电导峰还会逐渐消失; 耦合强度继续增大, 剩存的电导峰又逐渐变高变窄, 并在强耦合极限下与不包含两端原子的新孤立系统的能量本征值一一对应. 体态和边缘态对引线-样品耦合强度变化的不同响应可作为区分边缘态与体态的有效途径, 亦可作为系统中存在边缘态的重要判据.
-
关键词:
- Landauer电导 /
- Su-Schriefer-Heeger晶格 /
- 边缘态
The electronic eigen-energy and the Landauer conductance of the finite Su-Schriefer-Heeger (SSH) lattice are calculated carefully, and the different effects of the lead-sample coupling strength on the conductance peaks of the bulk states and edge states are investigated. Only under the weak coupling limit, can the conductance peaks demonstrate the eigen-energy of all bulk states and edge states. With the increase of coupling strength, all the conductance peaks gradually deviate from their corresponding eigen-energy values and become wider, and the conductance peaks of the edge states will gradually disappear. In particular, after the coupling strength continues to increase to a large enough value, the conductance peaks gradually narrow again, but two of the peaks disappear, and the survival peaks will correspond to the eigen-energy of the remaining lattice system that does not contain the two atoms at both ends under the strong coupling limit. Therefore, the different responses of the conductance peaks to the varying coupling strength can be used to distinguish edge state from bulk states, and judge whether a system has any edge states.-
Keywords:
- Landauer conductance /
- Su-Schriefer-Heeger lattice /
- edge state
[1] 蔚涛, 张路, 罗懋康 2013 物理学报 62 120504
Google Scholar
Yu T, Zhang L, Luo M K 2013 Acta Phys. Sin. 62 120504
Google Scholar
[2] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press) pp57–110
[3] Imry Y, Landauer R 1999 Rev. Mod. Phys. 71 S306
Google Scholar
[4] Wees B J, Houten H, Beenakker C W J, Williamson J G, Kouwenhoven L P, Marel D, Foxon C T 1988 Phys. Rev. Lett. 60 848
Google Scholar
[5] Berggren K F, Ji Z L 1991 Phys. Rev. B 43 4760
Google Scholar
[6] Sprung D W L, Wu H, Martorell J 1996 Am. J. Phys. 64 136
Google Scholar
[7] Bosken M, Steller A, Waring B, Cahay M 2014 Physica E Low Dimens. Syst. Nanostruct. 64 141
Google Scholar
[8] Ramírez C, González F H, Galván C G 2019 J. Phys. Soc. Jpn. 88 094002
Google Scholar
[9] Xu H Q 1993 Phys. Rev. B 47 9537
Google Scholar
[10] Ji Z L 1994 Phys. Rev. B 50 4658
Google Scholar
[11] Kawamura T, Leburton J P 1993 Phys. Rev. B 48 8857
Google Scholar
[12] Zhang H, Liu D E, Wimmer M, Kouwenhoven L P 2019 Nat. Commun. 10 5128
Google Scholar
[13] 于春霖, 张浩 2020 物理学报 69 077303
Google Scholar
Yu C L, Zhang H 2020 Acta Phys. Sin. 69 077303
Google Scholar
[14] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 物理学报 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[15] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 物理学报 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[16] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp1–99
[17] 卢曼昕, 邓文基 2019 物理学报 68 120301
Google Scholar
Lu M X, Deng W J 2019 Acta Phys. Sin. 68 120301
Google Scholar
[18] Kurzyna M, Kwapiński T 2020 Phys. Rev. B 102 195429
Google Scholar
[19] Zhang K L, Jin L, Song Z 2019 Phys. Rev. B 100 144301
Google Scholar
[20] Zhang K L, Song Z 2020 Phys. Rev. A 101 032111
[21] Haller A, Massignan P, Rizzi M 2020 Phys. Rev. Res. 2 033200
Google Scholar
[22] Kuno Y 2019 Phys. Rev. B 99 064105
Google Scholar
[23] Chen R, Chen C Z, Zhou B, Xu D H 2019 Phys. Rev. B 99 155431
Google Scholar
[24] Obana D, Liu F, Wakabayashi K 2019 Phys. Rev. B 100 075437
Google Scholar
[25] Weber M, Assaad F F, Hohenadler M 2015 Phys. Rev. B 91 245147
Google Scholar
[26] Yu W G, Sacramento P D, Li Y C, Angelakis D G, Lin H Q 2019 Phys. Rev. B 99 115113
Google Scholar
[27] Zhang S L, Zhou Q 2017 Phys. Rev. A 95 061601
Google Scholar
[28] 邓伟胤, 朱瑞, 邓文基 2013 物理学报 62 067301
Google Scholar
Deng W Y, Zhu R, Deng W J 2013 Acta Phys. Sin. 62 067301
Google Scholar
[29] Ajoy A, Karmalkar S 2010 J. Phys. Condens. Matter 22 435502
Google Scholar
-
图 1 (a)有限SSH晶格示意图; (b)引线和有限SSH晶格耦合系统示意图. 红色圆点表示A原子, 蓝色表示B原子, 黄色表示引线中的原子,
${t_v}$ 表示原胞内跃迁能,${t_w}$ 表示原胞间跃迁能Fig. 1. (a) Schematic diagram of the finite SSH lattice; (b) schematic diagram of lead and finite SSH lattice coupling system. The red dot represents the A atom, the blue dot represents the B atom, and the yellow dot represents the atom in the lead;
${t_v}$ indicates the intracell hopping, and${t_w}$ indicates intercell hopping.
图 2 不同耦合强度有限简单晶格的电导谱, 其中格点数
$2 N = 20$ , 跃迁能$t = 0.8$ Fig. 2. Conductance spectrum of the finite simple lattice with different coupling strengths, where the number of sizes
$2 N = 20$ , hopping$t = 0.8$ .
图 3 完整原胞数
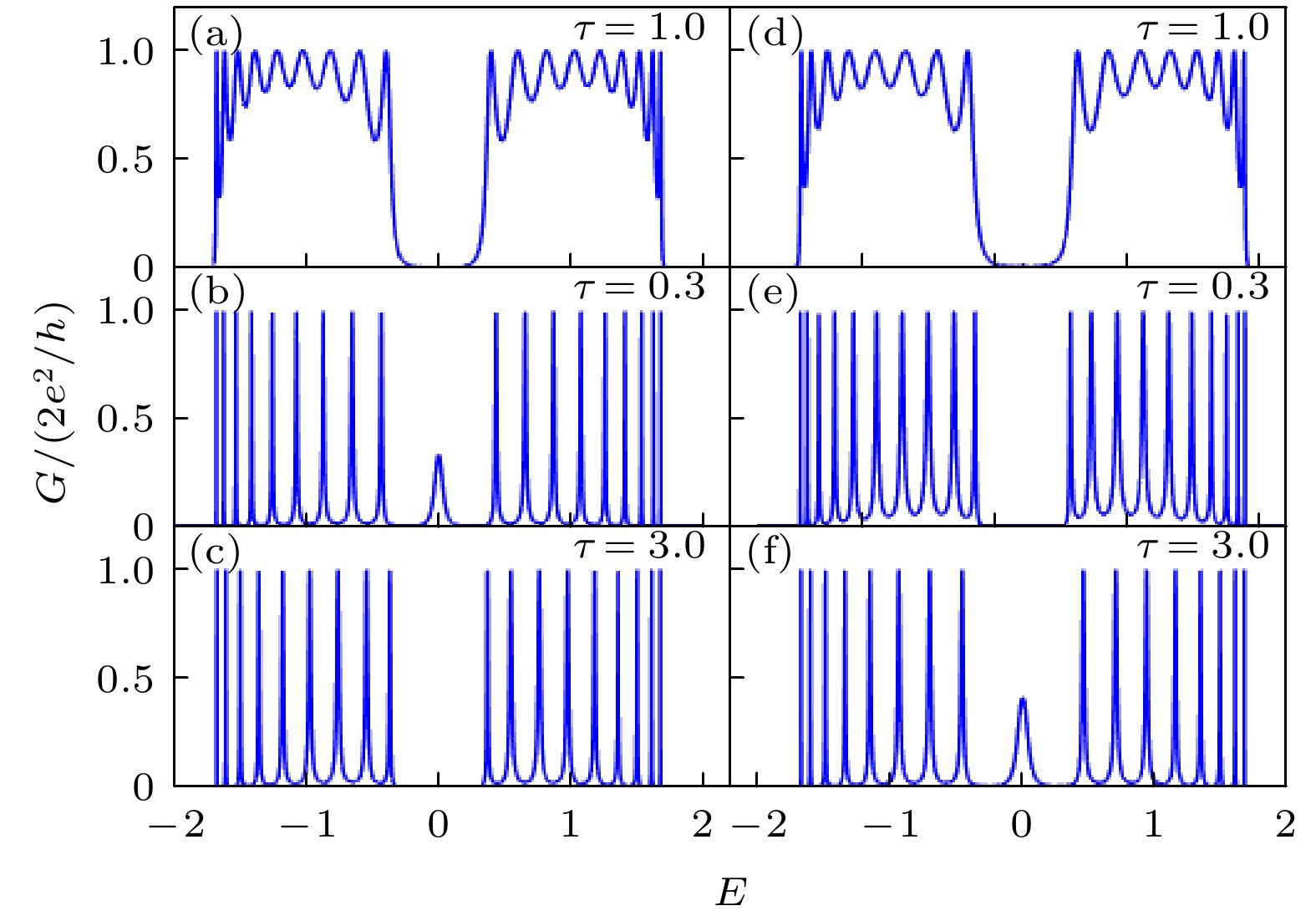
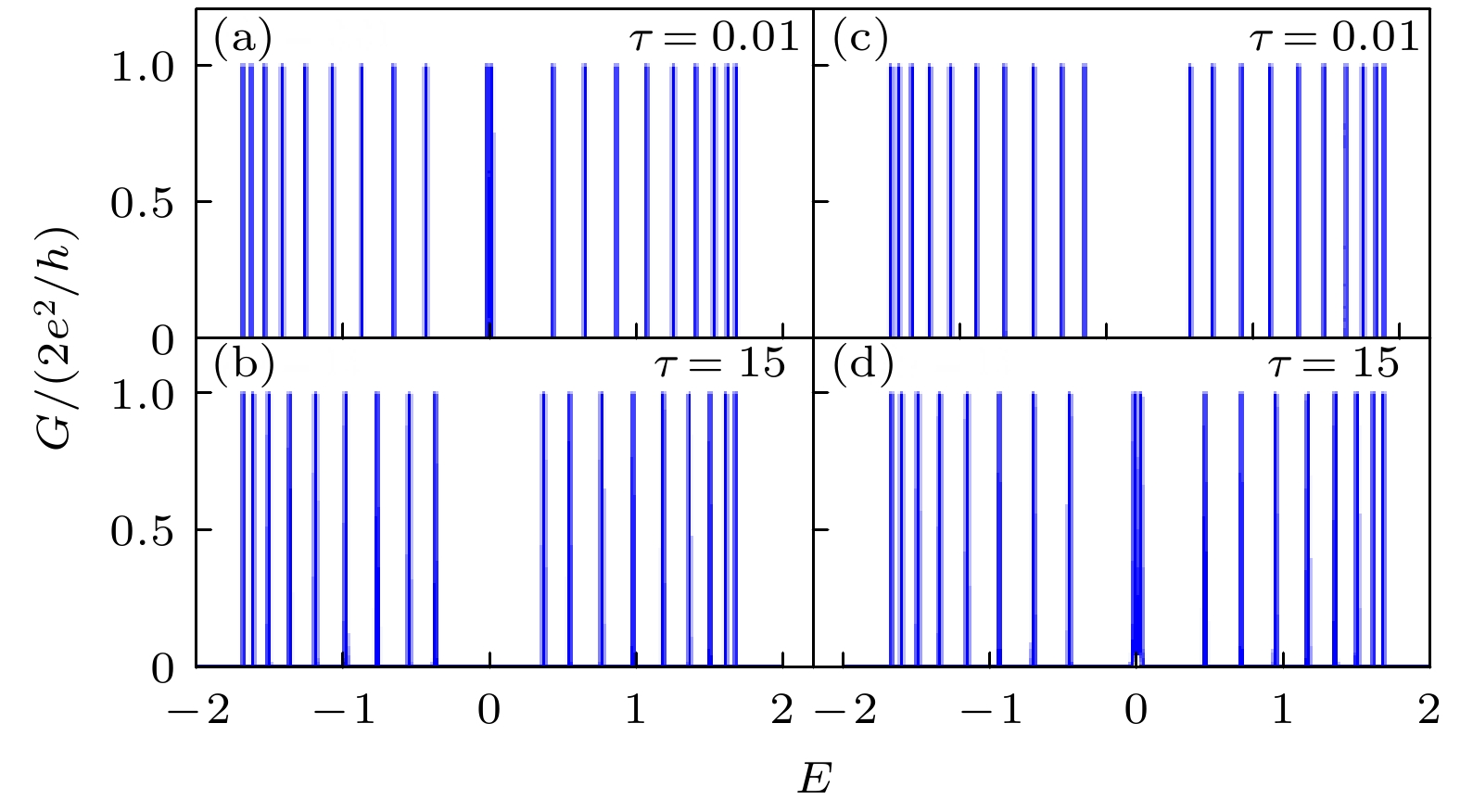
$N = 10$ 时有限SSH晶格的电导谱 (a)—(c)跃迁能${t_v} = 0.7$ ,${t_w} = 1$ ,$\tau = 1, 0.3, 3$ ; (d)—(f)跃迁能${t_v} = 1$ ,${t_w} = 0.7$ ,$\tau = 1, 0.3, 3.$ Fig. 3. Conductance spectrum of the finite SSH lattice with the number of cells
$N = 10$ : (a)–(c)${t_v} = 0.7, {t_w} = 1$ ,$\tau = 1, 0.3, 3$ ; (d)–(f)${t_v} = 1, {t_w} = 0.7$ ,$\tau = 1, 0.3, 3.$ 
图 4 弱耦合与强耦合极限下,
$N = 10$ 时有限SSH晶格的电导谱 (a)(b)${t_v} = 0.7, {t_w} = 1$ ; (c) (d)${t_v} = 1, {t_w} = 0.7$ Fig. 4. Conductance spectrum of the finite SSH lattice under the weak coupling limit and strong coupling limit with
$N = 10$ : (a) (b)${t_v} = 0.7, {t_w} = 1$ ; (c)(d)${t_v} = 1, {t_w} = 0.7$ 
图 5 有限SSH晶格电导峰随耦合强度的变化, 原胞数
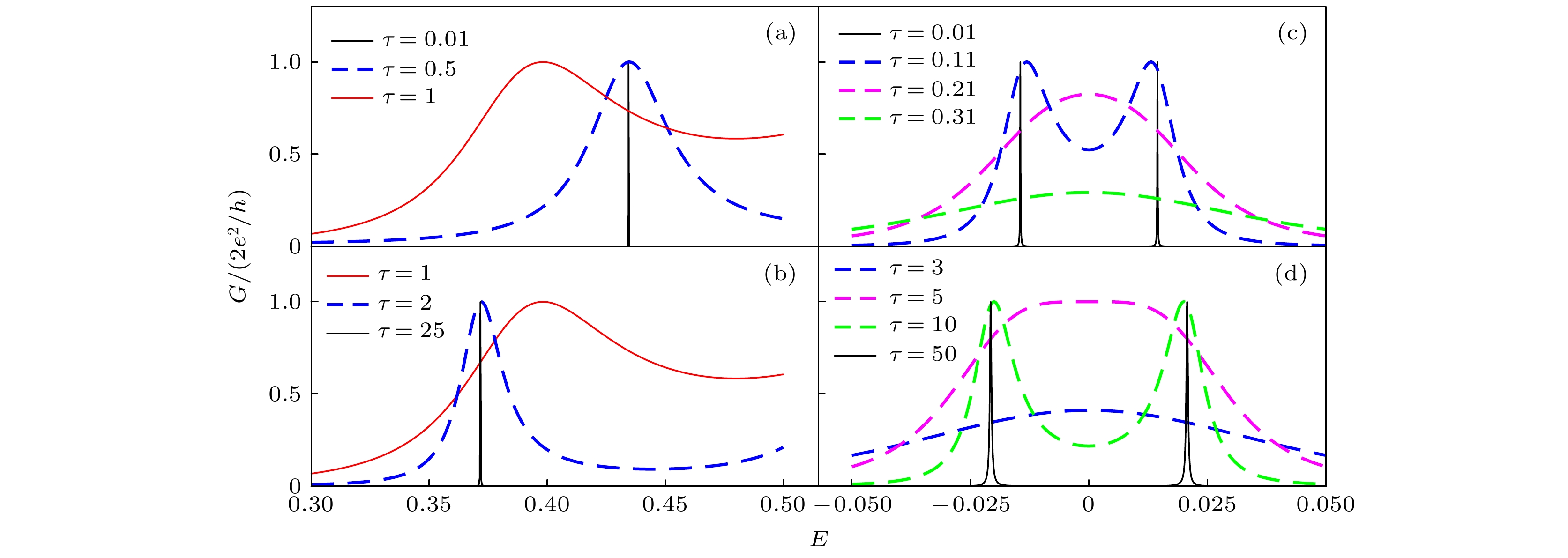
$N = 10$ (a)(b)${t_v} = 0.7$ ,${t_w} = 1$ 晶格的体态电导峰从弱耦合到强耦合$\tau = 0.01, 0.5, 1, 2, 25$ 的变迁; (c)${t_v} = 0.7$ ,${t_w} = 1$ 晶格在弱耦合情形$\tau = 0.01, 0.11, 0.21, 0.31$ 下的边缘态电导峰; (d)${t_v} = 1$ ,${t_w} = 0.7$ 晶格在强耦合情形$\tau = 3, 5, 10, 50$ 下的边缘态电导峰Fig. 5. The conductance peaks of the finite SSH lattice varies with the coupling strength for
$N = 10$ : (a)(b)${t_v} = 0.7, {t_w} = 1$ ,$\tau = 0.01, 0.5, 1, 2, 25$ , the conductance peaks of the bulk states varies with the coupling strength from weak coupling to strong coupling; (c)${t_v} = 0.7$ ,${t_w} = 1$ $\tau = 0.01, 0.11, 0.21, 0.31$ , the conductance peaks of the edge states varies with the coupling strength under the weak coupling limit; (d)${t_v} = 1$ ,${t_w} = 0.7$ ,$\tau = 3, 5, 10, 50$ , the conductance peaks of the edge states varies with the coupling strength under the strong coupling limit. -
[1] 蔚涛, 张路, 罗懋康 2013 物理学报 62 120504
Google Scholar
Yu T, Zhang L, Luo M K 2013 Acta Phys. Sin. 62 120504
Google Scholar
[2] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press) pp57–110
[3] Imry Y, Landauer R 1999 Rev. Mod. Phys. 71 S306
Google Scholar
[4] Wees B J, Houten H, Beenakker C W J, Williamson J G, Kouwenhoven L P, Marel D, Foxon C T 1988 Phys. Rev. Lett. 60 848
Google Scholar
[5] Berggren K F, Ji Z L 1991 Phys. Rev. B 43 4760
Google Scholar
[6] Sprung D W L, Wu H, Martorell J 1996 Am. J. Phys. 64 136
Google Scholar
[7] Bosken M, Steller A, Waring B, Cahay M 2014 Physica E Low Dimens. Syst. Nanostruct. 64 141
Google Scholar
[8] Ramírez C, González F H, Galván C G 2019 J. Phys. Soc. Jpn. 88 094002
Google Scholar
[9] Xu H Q 1993 Phys. Rev. B 47 9537
Google Scholar
[10] Ji Z L 1994 Phys. Rev. B 50 4658
Google Scholar
[11] Kawamura T, Leburton J P 1993 Phys. Rev. B 48 8857
Google Scholar
[12] Zhang H, Liu D E, Wimmer M, Kouwenhoven L P 2019 Nat. Commun. 10 5128
Google Scholar
[13] 于春霖, 张浩 2020 物理学报 69 077303
Google Scholar
Yu C L, Zhang H 2020 Acta Phys. Sin. 69 077303
Google Scholar
[14] 张蓝云, 薛海斌, 陈彬, 陈建宾, 邢丽丽 2020 物理学报 69 077301
Google Scholar
Zhang L Y, Xue H B, Chen B, Chen J B, Xing L L 2020 Acta Phys. Sin. 69 077301
Google Scholar
[15] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 物理学报 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[16] Asbóth J K, Oroszlány L, Pályi A 2016 A Short Course on Topological Insulators (Budapest: Springer) pp1–99
[17] 卢曼昕, 邓文基 2019 物理学报 68 120301
Google Scholar
Lu M X, Deng W J 2019 Acta Phys. Sin. 68 120301
Google Scholar
[18] Kurzyna M, Kwapiński T 2020 Phys. Rev. B 102 195429
Google Scholar
[19] Zhang K L, Jin L, Song Z 2019 Phys. Rev. B 100 144301
Google Scholar
[20] Zhang K L, Song Z 2020 Phys. Rev. A 101 032111
[21] Haller A, Massignan P, Rizzi M 2020 Phys. Rev. Res. 2 033200
Google Scholar
[22] Kuno Y 2019 Phys. Rev. B 99 064105
Google Scholar
[23] Chen R, Chen C Z, Zhou B, Xu D H 2019 Phys. Rev. B 99 155431
Google Scholar
[24] Obana D, Liu F, Wakabayashi K 2019 Phys. Rev. B 100 075437
Google Scholar
[25] Weber M, Assaad F F, Hohenadler M 2015 Phys. Rev. B 91 245147
Google Scholar
[26] Yu W G, Sacramento P D, Li Y C, Angelakis D G, Lin H Q 2019 Phys. Rev. B 99 115113
Google Scholar
[27] Zhang S L, Zhou Q 2017 Phys. Rev. A 95 061601
Google Scholar
[28] 邓伟胤, 朱瑞, 邓文基 2013 物理学报 62 067301
Google Scholar
Deng W Y, Zhu R, Deng W J 2013 Acta Phys. Sin. 62 067301
Google Scholar
[29] Ajoy A, Karmalkar S 2010 J. Phys. Condens. Matter 22 435502
Google Scholar
下载:
计量
- 文章访问数: 5886
- PDF下载量: 96
- 被引次数: 0
