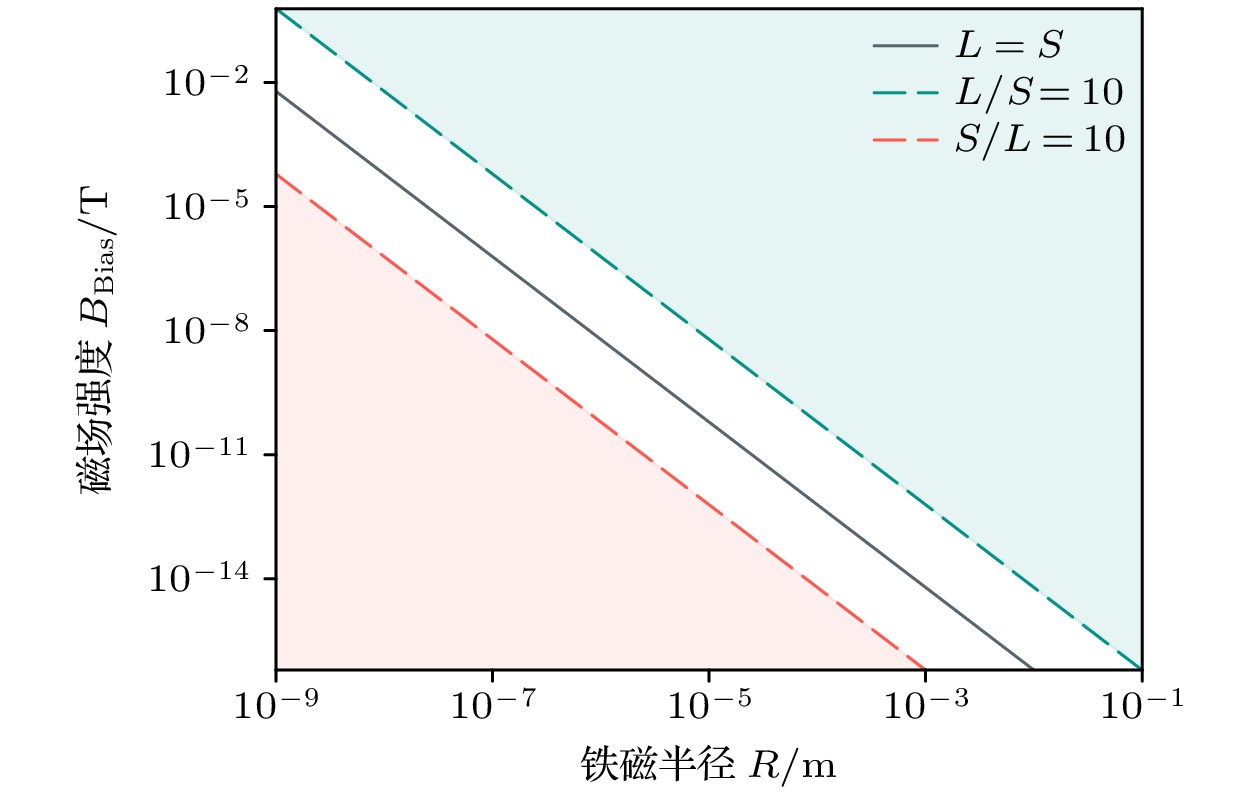
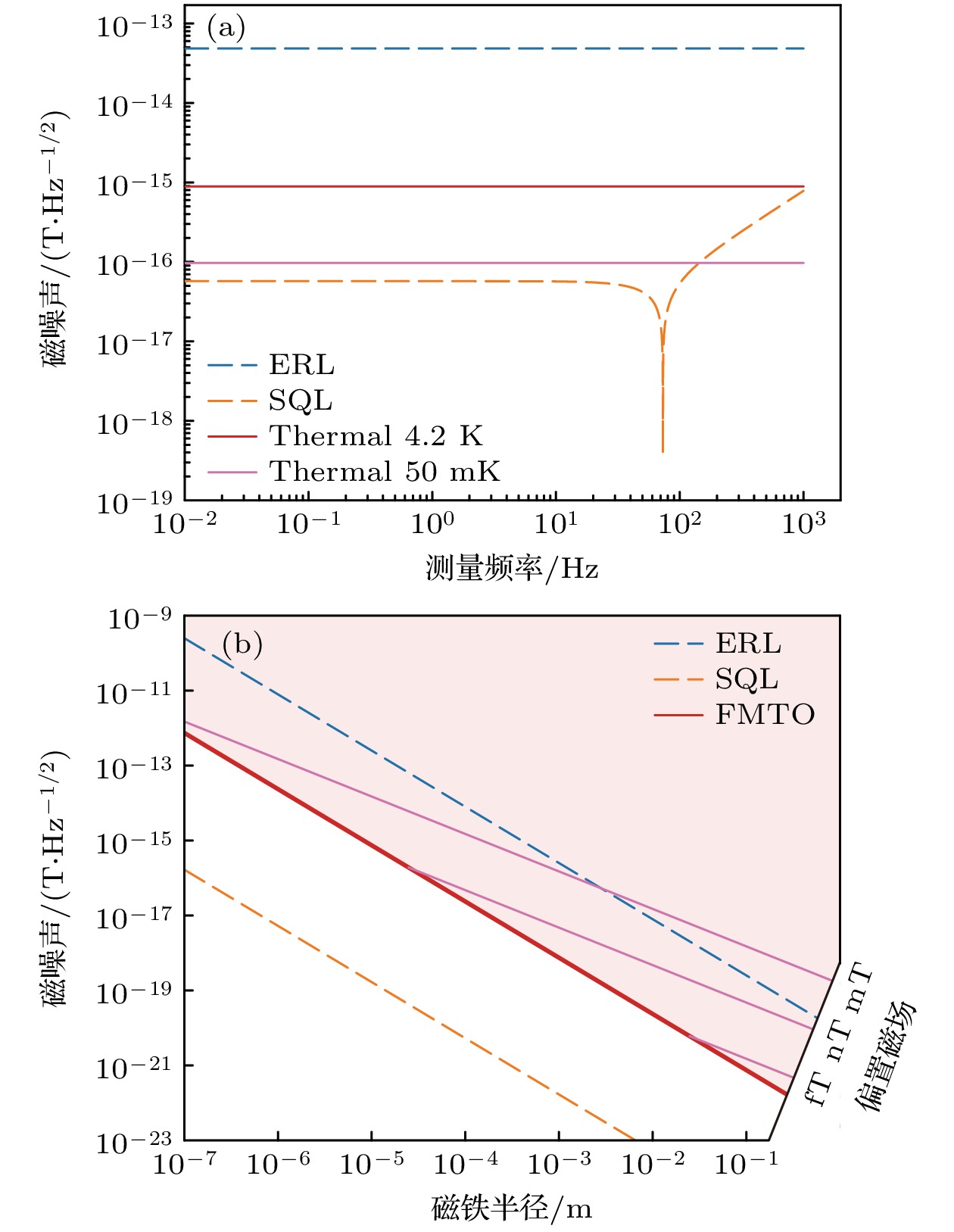
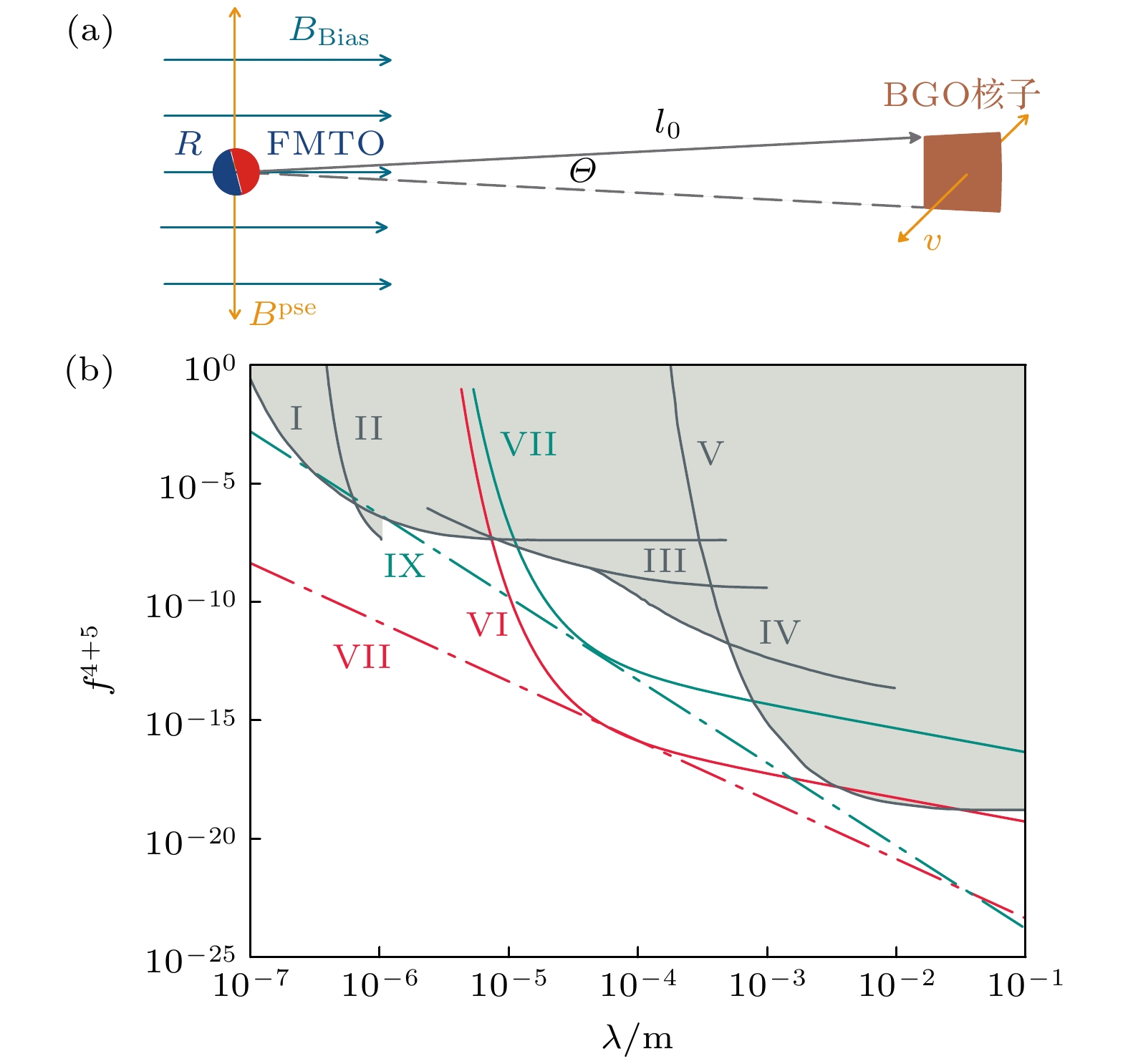
-
The ferromagnetic-mechanical system can be used as a magnetometer by monitoring its mechanical response to magnetic signals. This system can exceed the energy resolution limit (ERL) in terms of sensitivity, due to the ultra-high spin density and strong spin-lattice interactions inherent in ferromagnetic materials. A levitated ferromagnetic-mechanical system can further enhance its quality factor by eliminating clamp dissipation, thus achieving higher magnetic sensitivity. In this work, a magnetometer is proposed based on a magnetically levitated ferromagnetic torsional oscillator (FMTO), which transforms magnetic signals into torque to drive the oscillator. An optical method is then used to measure the torsional motion and extract the magnetic signal. The resonance frequency of this FMTO system can be controlled by modifying the bias field, thus providing enhanced flexibility and control. By analyzing the influence of fundamental noise, including thermal noise and quantum measurement noise (SQL), the relationship between the magnetic noise floor of the FMTO made of NdFeB and its radius is obtained. The SQL is much lower than both thermal noise and ERL, indicating that thermal noise is a dominant factor affecting the magnetic sensitivity of the FMTO. The magnetic sensitivity of the FMTO system at $4.2\ \rm{K}$ exceeds the ERL by three orders of magnitude, confirming the significant potential application of the FMTO system in high-precision magnetic measurements. Searching for exotic interactions is one of the most promising applications of ultra-high sensitivity magnetic sensors. It is typically achieved by measuring pseudo-magnetic fields. The accuracy of detecting exotic interactions depends on two main factors: the magnetometer's sensitivity and the distance between the sensor and the source. The ERL presents challenges in meeting both of these factors simultaneously. Improving magnetic sensitivity typically increases the radius of the sensor, which in turn increases the distance between the sensor and the source, limiting the accuracy of detecting exotic interactions. Thus, ERL limits the accuracy of exotic interaction detection, while the FMTO, with its excellent sensitivity, is expected to significantly improve the detection of exotic interactions. If there is an exotic interaction, the BGO nuclei oscillating perpendicular to the paper will generate a pseudo-magnetic field along the vertical direction. This pseudo-magnetic field will induce torsional motion in the FMTO. The lower limit of the coupling constant for the new interaction is determined by measuring the torsional motion. Existing experiments have approached the ERL at Compton wavelengths on millimeter and micrometer scales. However, the FMTO system, with a bias field of $1\ \rm{\mu T}$, exceeds the ERL by up to five orders of magnitude in sub-centimeter Compton wavelength and the existing experimental results by two to nine orders of magnitude. These results highlight the potential advantages of FMTO-based magnetometers in probing exotic interactions. All in all, in this work, a magnetometer configuration is proposed based on a levitated FMTO and its mechanical response, fundamental noise, magnetic performance, and applications in fundamental research are analyzed comprehensively. -
Keywords:
- magnetometer /
- ferromagnetic oscillator /
- precision measurement /
- exotic interactions
-
图 1 铁磁球体在磁场中的运动模式: 铁磁扭摆振子(左图)和铁磁陀螺(右图)
Figure 1. The patterns of ferromagnetic magnets in a magnetic field: ferromagnetic orsion pendulum oscillator (left panel) and ferromagnetic gyroscope (right panel).
图 2 铁磁半径及外磁场对运动模式的影响
Figure 2. Ferromagnets' motion pattern decided by external field and its radius.
图 3 (a). FMTO磁噪声与测量频率关系: ERL噪声(蓝虚线), SQL噪声(橙虚线), $ 4.2\ {\rm{K}} $热噪声(红实线)与$ 50\ {\rm{mK}} $热噪声(粉实线); (b). FMTO磁噪声本底与半径关系: ERL噪声(蓝虚线), 共振时SQL噪声(橙虚线), $ 4.2\ {\rm{K}} $ FMTO热噪声极限(红实线), 特定磁场下$ 4.2\ {\rm{K}} $ FMTO热噪声(粉实线)
Figure 3. (a). Magnetic noise versus frequency for FMTO: ERL (blue dashed), SQL (orange dashed), Thermal at $ 4.2\ {\rm{K}} $ (red solid) and at $ 50\ {\rm{m K}} $ (pink solid); (b). Magnetic noise versus radius for FMTO: ERL (blue dashed), resonant SQL (orange dashed), Thermal limit at $ 4.2\ {\rm{K}} $ (red solid) and with special bias field (pink solid).
图 4 (a) 新相互作用探测示意图; (b) 新相互作用探测: I[34], II[33], III[35], IV[36], V[37]均为实验结果, VI和VII分别对应FMTO和ERL固定间距下探测结果, VIII和IX分别代表FMTO和ERL的最优结果
Figure 4. (a) Schematic of the detection of exotic interactions; (b) Exotic interactions probes: I[34], II[33], III[35], IV[36], V[37], all are experimental results; VI and VII are the results acheived by FMTO and ERL under fixed pitch respectively, VI and VII are the optimal results of VIII and IX respectively.
-
[1] Xia H, Ben Amar Baranga A, Hoffman D, Romalis M V 2006 Appl. Phys. Lett. 89 211104
Google Scholar
[2] Harada S, Sasada I, Hang F 2015 Electr. Commun. Jap. 98 20
[3] Dolabdjian C, Saez S, Reyes Toledo A, Robbes D 1998 Rev. Sci. Instrum. 69 3678
Google Scholar
[4] Germain-Jones D T 1957 J. Sci. Instrum. 34 1
Google Scholar
[5] Mohanty I, Nagendran R, Arasu A V T, Baskaran R, Mani A 2018 Meas. Sci. Technol. 29 105601
Google Scholar
[6] Nabighian M N, Grauch V J S, Hansen R O, LaFehr T R, Li Y, Peirce J W, Phillips J D, Ruder M E 2005 Geophysics 70 33
[7] 赵龙, 颜廷君 2013 物理学报 62 067702
Google Scholar
Zhao L, Yan T J 2013 Acta Phys. Sin. 62 067702
Google Scholar
[8] Pedersen L W, Merenyi L 2016 J. Ind. Geophys. Union. 2 30
[9] Jiang M, Su H W, Garcon A, Peng X H, Budker D 2021 Nat. Phys. 17 1402
Google Scholar
[10] Wang Y H, Huang Y, Guo C, Jiang M, Kang X, Su H W, Qin Y S, Ji W, Hu D D, Peng X H, Budker D 2023 Sci. Adv. 9 eade0353
Google Scholar
[11] Wang Y H, Su H W, Jiang M, Huang Y, Qin Y H, Guo C, Wang Z H, Hu D D, Ji W, Fadeev P, Budker D 2022 Phys. Rev. Lett. 129 051801
Google Scholar
[12] Su H W, Wang Y H, Jiang M, Ji W, Fadeev P, Hu D D, Peng X H, Budker D 2021 Sci. Adv. 7 eabi9535
Google Scholar
[13] Braginsky V B 1968 Sov. Phys. Jetp. 26 831
[14] Braginsky V B, Vorontsov Y I 1975 Sov. Phys. Usp. 17 644
Google Scholar
[15] Mitchell M W, Palacios Alvarez S 2020 Rev. Mod. Phys. 92 021001
Google Scholar
[16] Vinante A, Timberlake C, Budker D, Kimball D F J, Sushkov A O, Ulbricht H 2021 Phys. Rev. Lett. 127 070801
Google Scholar
[17] Vinante A, Falferi P, Gasbarri G, Setter A, Timberlake C, Ulbricht H 2020 Phys. Rev. Appl. 13 064027
Google Scholar
[18] Jackson Kimball D F, Sushkov A O, Budker D 2016 Phys. Rev. Lett. 116 190801
Google Scholar
[19] Fadeev P, Wang T, Band Y B, Budker D, Graham P W, Sushkov A O, Kimball D F J 2021 Phys. Rev. D 103 044056
Google Scholar
[20] Fadeev P, Timberlake C, Wang T, Vinante A, Band Y B, Budker D, Sushkov A O, Ulbricht H, Kimball D F J 2021 Quantum. Sci. Technol. 6 024006
Google Scholar
[21] 张莉, 刘立, 曹力 2010 物理学报 59 1494
Google Scholar
Zhang L, Liu L, Cao L 2010 Acta Phys. Sin. 59 1494
Google Scholar
[22] Slezak B R, Lewandowski C W, Hsu J F, D Urso B 2018 New J. Phys. 20 063028
Google Scholar
[23] Timberlake C, Gasbarri G, Vinante A, Setter A, Ulbricht H 2019 Appl. Phys. Lett. 115 224101
Google Scholar
[24] Zheng D, Leng Y C, Kong X, Li R, Wang Z Z, Luo X H, Zhao J, Duan C K, Huang P, Du J F, Matteo C, Bassi A 2020 Phys. Rev. Res. 2 013057
Google Scholar
[25] Gieseler J, Novotny L, Quidant R 2013 Nat. Phys. 9 806
Google Scholar
[26] Millen J, Fonseca P Z G, Mavrogordatos T, Monteiro T S, Barker P F 2015 Phys. Rev. Lett. 114 123602
Google Scholar
[27] Wang T, Lourette S, O Kelley S R, Kayci M, Band Y B, Kimball D F J, Sushkov A O, Budker D 2019 Phys. Rev. Appl. 11 044041
Google Scholar
[28] Schloss J M, Barry J F, Turner M J, Walsworth R L 2018 Phys. Rev. Appl. 10 034044
Google Scholar
[29] Callen H B, Welton T A 1951 Phys. Rev. 83 34
Google Scholar
[30] Nimmrichter S, Hornberger K, Hammerer K 2014 Phys. Rev. Lett. 113 020405
Google Scholar
[31] Losby J E, Freeman M R 2016 arXiv:1601.00674
[32] Leslie T M, Weisman E, Khatiwada R, Long J C 2014 Phys. Rev. D 89 114022
Google Scholar
[33] Wu L H, Lin S C, Kong X, Wang M Q, Zhou J W, Duan C K, Huang P, Zhang L, Du J F 2023 PNAS 120 e2302145120
Google Scholar
[34] Ding J H, Wang J B, Zhou X, Liu Y, Sun K, Adeyeye A O, Fu H X, Ren X F, Li S M, Luo P S, Lan Z, Yang S Q, Luo J 2020 Phys. Rev. Lett. 124 161801
Google Scholar
[35] Wu D G, Liang H, Jiao M, Cai Y F, Duan C K, Wang Y, Rong X, Du J F 2023 Phys. Rev. Lett. 131 071801
Google Scholar
[36] Piegsa F M, Pignol G 2012 Phys. Rev. Lett. 108 181801
Google Scholar
[37] Kim Y J, Chu P H, Savukov I 2018 Phys. Rev. Lett. 121 091802
Google Scholar
DownLoad:
Metrics
- Abstract views: 241
- PDF Downloads: 12
- Cited By: 0
